La siguiente prueba t de dos muestras se generó para el conjunto de datos AUTO83B.DAT. El conjunto de datos contiene millas por galón para automóviles estadounidenses (muestra 1) y para automóviles japoneses (muestra 2); a continuación se muestran las estadísticas de resumen para cada muestra.
SAMPLE 1: NUMBER OF OBSERVATIONS = 249 MEAN = 20.14458 STANDARD DEVIATION = 6.41470 STANDARD ERROR OF THE MEAN = 0.40652 SAMPLE 2: NUMBER OF OBSERVATIONS = 79 MEAN = 30.48101 STANDARD DEVIATION = 6.10771 STANDARD ERROR OF THE MEAN = 0.68717
Estamos probando la hipótesis de que las medias poblacionales son iguales para las dos muestras. Suponemos que las varianzas de las dos muestras son iguales.
El valor absoluto del estadístico de prueba para nuestro ejemplo, 12,62059, es mayor que el valor crítico de 1,9673, por lo que rechazamos la hipótesis nula y concluimos que las dos medias poblacionales son diferentes al nivel de significación de 0,05.
En general, hay tres posibles hipótesis alternativas y regiones de rechazo para la prueba t de una muestra:
| Hipótesis alternativa | Región de rechazo |
|---|---|
| Ha: μ1 ≠ μ2 | |T| > t1-α/2,ν | Ha: μ1 > μ2 | T > t1-α,ν |
| Ha: μ1 2 | T tα,ν |
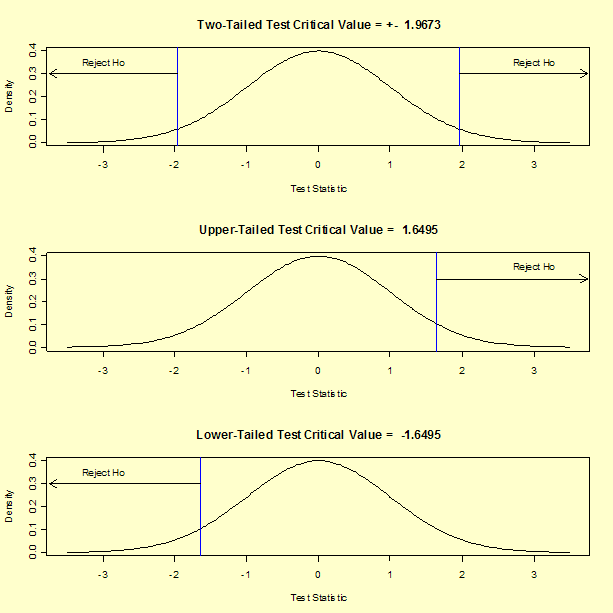
Para nuestra prueba t de dos colas, el valor crítico es t1-α/2,ν = 1.9673, donde α = 0,05 y ν = 326. Si realizáramos una prueba superior de una cola, el valor crítico sería t1-α,ν = 1,6495.A continuación se muestran las regiones de rechazo para tres posibles hipótesis alternativas utilizando nuestros datos de ejemplo.
0 comentarios