Il seguente test t a due campioni è stato generato per il set di dati AUTO83B.DAT. Il set di dati contiene miglia per gallone per le auto americane (campione 1) e per le auto giapponesi (campione 2); le statistiche riassuntive per ogni campione sono mostrate di seguito.
SAMPLE 1: NUMBER OF OBSERVATIONS = 249 MEAN = 20.14458 STANDARD DEVIATION = 6.41470 STANDARD ERROR OF THE MEAN = 0.40652 SAMPLE 2: NUMBER OF OBSERVATIONS = 79 MEAN = 30.48101 STANDARD DEVIATION = 6.10771 STANDARD ERROR OF THE MEAN = 0.68717
Stiamo testando l’ipotesi che le medie della popolazione siano uguali per i due campioni. Assumiamo che le varianze dei due campioni siano uguali.
Il valore assoluto della statistica del test per il nostro esempio, 12,62059, è maggiore del valore critico di 1,9673, quindi rifiutiamo l’ipotesi nulla e concludiamo che le due medie della popolazione sono diverse al livello di significatività 0,05.
In generale, ci sono tre possibili ipotesi alternative e regioni di rifiuto per il test t a un campione:
| Ipotesi alternative | Regione di rifiuto |
|---|---|
| Ha: μ1 ≠ μ2 | |T| > t1-α/2,ν |
| Ha: μ1 > μ2 | T > t1-α,ν |
| Ha: μ1 2 | T tα,ν |
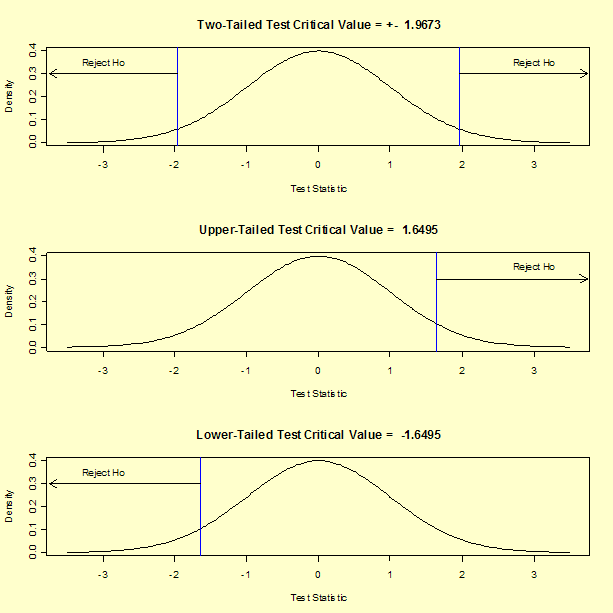
Per il nostro test t a due code, il valore critico è t1-α/2,ν = 1.9673, dove α = 0,05 e ν = 326. Se dovessimo eseguire un test superiore a una coda, il valore critico sarebbe t1-α,ν = 1,6495.Le regioni di rigetto per tre possibili ipotesi alternative utilizzando i nostri dati di esempio sono mostrate qui sotto.
0 commenti