O seguinte teste t de duas amostras foi gerado para o conjunto de dados AUTO83B.DAT. O conjunto de dados contém milhas por galão para carros dos EUA (amostra 1) e para carros japoneses (amostra 2); as estatísticas resumidas para cada amostra são mostradas abaixo.
SAMPLE 1: NUMBER OF OBSERVATIONS = 249 MEAN = 20.14458 STANDARD DEVIATION = 6.41470 STANDARD ERROR OF THE MEAN = 0.40652 SAMPLE 2: NUMBER OF OBSERVATIONS = 79 MEAN = 30.48101 STANDARD DEVIATION = 6.10771 STANDARD ERROR OF THE MEAN = 0.68717
Estamos a testar a hipótese de que os meios da população são iguais para as duas amostras. Assumimos que as variâncias para as duas amostras são iguais.
O valor absoluto da estatística do teste para o nosso exemplo, 12,62059, é superior ao valor crítico de 1,9673, pelo que rejeitamos a hipótese nula e concluímos que as duas médias da população são diferentes ao nível de significância de 0,05.
Em geral, há três hipóteses alternativas possíveis e regiões de rejeição para o teste t de uma amostra:
| Alternative Hypothesis | Rejection Region |
|---|---|
| Ha: μ1 ≠ μ2 | |T| > t1-α/2,ν |
| Ha: μ1 > μ2 | T > t1-α,ν |
| Ha: μ1 2 | T tα,ν |
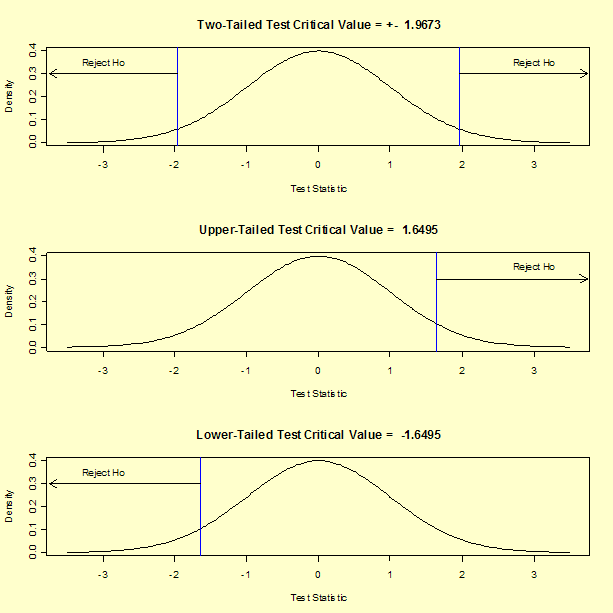
Para o nosso teste t de duas caudas, o valor crítico é t1-α/2,ν = 1.9673, onde α = 0,05 e ν = 326. Se realizássemos um teste superior de uma cauda, o valor crítico seria t1-α,ν = 1.6495.As regiões de rejeição para três hipóteses alternativas possíveis usando os nossos dados de exemplo são mostradas abaixo.
0 comentários