Ley de Hess

Por qué funciona

Una vista pictórica de la Ley de Hess aplicada al calor de la ecuación es ilustrativa. En la figura 1, los reactivos C(s) + 2 H2O(g) se colocan juntos en una caja, representando el estado de los materiales involucrados en la reacción antes de la misma. Los productos CO2(g) + 2 H2(g) se colocan juntos en una segunda caja que representa el estado de los materiales implicados después de la reacción. La flecha de reacción que conecta estas cajas está etiquetada con el calor de esta reacción. Ahora tomamos estos mismos materiales y los colocamos en una tercera caja que contiene C(s), O2(g) y 2 H2(g). Esta caja está conectada a las cajas del reactante y del producto con flechas de reacción, etiquetadas con los calores de reacción en la ecuación y la ecuación.

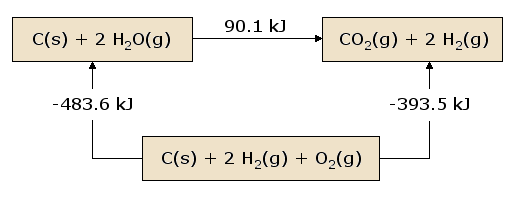
Esta imagen de la Ley de Hess revela que el calor de reacción a lo largo del «camino» que conecta directamente el estado del reactante con el estado del producto es exactamente igual al calor total de reacción a lo largo del «camino» alternativo que conecta los reactantes con los productos a través del estado intermedio que contiene \(C_(s)}, \(O_{2(g)}), y 2 \(H_{2(g)}). Una consecuencia de nuestra observación de la Ley de Hess es, por tanto, que el calor neto evolucionado o absorbido durante una reacción es independiente del camino que conecta el reactante con el producto (esta afirmación está de nuevo sujeta a nuestra restricción de que todas las reacciones en el camino alternativo deben ocurrir en condiciones de presión constante).

Una visión ligeramente diferente de la figura 1 resulta de comenzar en la caja del reactante y seguir un circuito completo a través de las otras cajas que conducen de nuevo a la caja del reactante, sumando los calores netos de reacción a medida que avanzamos. Descubrimos que el calor neto transferido (siempre que todas las reacciones se produzcan a presión constante) es exactamente cero. Esto es una afirmación de la conservación de la energía: la energía en el estado reactivo no depende de los procesos que produjeron ese estado. Por tanto, no podemos extraer ninguna energía de los reactantes mediante un proceso que simplemente recree los reactantes. Si no fuera así, podríamos producir infinitamente cantidades ilimitadas de energía siguiendo el camino tortuoso que reproduce continuamente los reactantes iniciales.

Por este razonamiento, podemos definir una función de energía cuyo valor para los reactantes es independiente de cómo se preparó el estado del reactante. Del mismo modo, el valor de esta función de energía en el estado de los productos es independiente de cómo se preparen los productos. Elegimos esta función, H, de forma que el cambio en la función, ΔH = Hproductos – Hreactantes, sea igual al calor de reacción q en condiciones de presión constante. H, que llamamos entalpía, es una función de estado, ya que su valor depende únicamente del estado de los materiales considerados, es decir, de la temperatura, la presión y la composición de estos materiales.

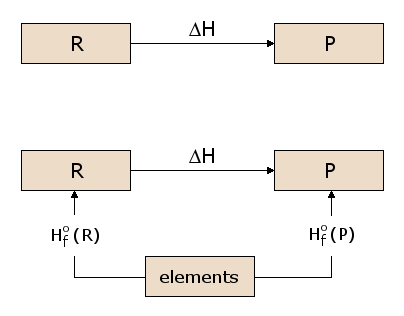
El concepto de función de estado es algo análogo a la idea de elevación. Consideremos la diferencia de elevación entre el primer piso y el tercer piso de un edificio. Esta diferencia es independiente del camino que elijamos para llegar del primer al tercer piso. Podemos simplemente subir dos tramos de escaleras, o subir un tramo de escaleras, recorrer el edificio a pie y luego subir un segundo tramo de escaleras. O podemos subir en el ascensor. Incluso podemos salir al exterior y hacer que una grúa nos eleve hasta el tejado del edificio, desde el que bajamos al tercer piso. Cada camino produce exactamente el mismo aumento de elevación, aunque la distancia recorrida es significativamente diferente de un camino a otro. Esto se debe simplemente a que la elevación es una «función de estado». Nuestra elevación, estando en el tercer piso, es independiente de cómo hayamos llegado al tercer piso, y lo mismo ocurre con el primer piso. Dado que la elevación es, por tanto, una función de estado, la ganancia de elevación es independiente del camino. Ahora bien, la existencia de una función de estado de energía H tiene una importancia considerable en el cálculo de los calores de reacción. Consideremos la reacción prototípica de la subfigura 2.1, en la que los reactivos R se convierten en productos P. Queremos calcular el calor absorbido o liberado en esta reacción, que es ΔH. Como H es una función de estado, podemos seguir cualquier camino desde R hasta P y calcular ΔH a lo largo de ese camino. En la subfigura 2.2, consideramos uno de esos posibles caminos, que consiste en dos reacciones que pasan por un estado intermedio que contiene todos los átomos implicados en la reacción, cada uno en forma elemental. Se trata de un estado intermedio útil, ya que puede utilizarse para cualquier reacción química posible. Por ejemplo, en la figura 1, los átomos implicados en la reacción son C, H y O, cada uno de los cuales está representado en el estado intermedio en forma elemental. Podemos ver en la subfigura 2.2 que el ΔH para la reacción global es ahora la diferencia entre el ΔH en la formación de los productos P a partir de los elementos y el ΔH en la formación de los reactivos R a partir de los elementos.

Los valores de ΔH para la formación de cada material a partir de los elementos son, por tanto, de utilidad general para calcular el ΔH de cualquier reacción de interés. Por lo tanto, definimos la reacción de formación estándar para el reactivo R, como

elementos en estado estánda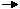r R

y el calor implicado en esta reacción es la entalpía de formación estándar, designada por ΔHf°. El subíndice f, que significa «formación», indica que la ΔH es para la reacción que crea el material a partir de los elementos en estado estándar. El superíndice ° indica que las reacciones se producen en condiciones de presión estándar constante de 1 atm. A partir de la subfigura 2.2, vemos que el calor de cualquier reacción puede calcularse a partir de

Se han compilado extensas tablas de valores de ΔH°f (Tabla T1) que nos permiten calcular con total confianza el calor de reacción para cualquier reacción de interés, incluso incluyendo reacciones hipotéticas que pueden ser difíciles de realizar o imposiblemente lentas de reaccionar.