Las bellezas que esconde Pi(π)

La razón lógica parece críptica; es que pi es una hermosa fuente para generar números aleatorios. Sin embargo, la verdadera razón parece ser para que los países puedan presumir de su tecnología ante otros países, ya que para calcular trillones de dígitos de pi se necesita un ordenador muy potente. Por ejemplo, en el episodio de Star Trek «Wolf in the Fold», Spock frustra al malvado ordenador ordenándole que «calcule hasta el último dígito el valor de Pi». Así que pedirle a un ordenador que calcule Pi se llama «una prueba de esfuerzo», y puede hacer que se estrelle.

Por otro lado, los humanos somos creadores torpes. Quedarnos en casa y beber té es una actividad hermosa, pero cuando nos aburrimos intentamos escalar la más alta de las montañas, enfrentarnos a un tigre o intento memorizar los dígitos de pi como Chao Lu, que memorizó correctamente los primeros 67.890 dígitos de pi. Seguiremos haciendo estas cosas porque nos gusta entender el mundo que nos rodea.

El 12 de septiembre de 1962, John F. Kennedy pronunció un discurso sobre el programa espacial. Dijo:

«Todavía no hay luchas, ni prejuicios, ni conflictos nacionales en el espacio exterior. Sus peligros son hostiles para todos nosotros. Su conquista merece lo mejor de toda la humanidad, y su oportunidad para la cooperación pacífica muchos no vuelven a aparecer. ¿Pero por qué, dicen algunos, la Luna? ¿Por qué elegirla como meta? Y bien pueden preguntar ¿por qué escalar la montaña más alta? Elegimos ir a la luna. Elegimos ir a la luna en esta década y hacer las otras cosas, no porque sean fáciles, sino porque son difíciles, porque esa meta servirá para organizar y medir lo mejor de nuestras energías y habilidades, porque ese reto es uno que estamos dispuestos a aceptar, uno que no estamos dispuestos a posponer, y uno que pretendemos ganar, y los otros también.

Estamos inevitablemente conectados con el pasado, y pi es un hilo que ha atravesado toda la historia de la humanidad. Por eso podemos decir que mientras haya gente, siempre habrá alguien que se pregunte qué es lo siguiente. Y te aseguro que en algún lugar del mundo hay un matemático o un científico utilizando pi para algo importante para nuestro universo porque pi sigue siendo la misteriosa constante de la naturaleza.

La afirmación anterior es totalmente cierta porque siempre ha habido alguien que trabaja sobre Pi. Las matemáticas son tan antiguas como la civilización. Pi ha sido estudiado por la raza humana desde hace casi 4000 años. Cuando los últimos mamuts se estaban extinguiendo, la gente estaba estudiando Pi. Por lo que sabemos, Arquímedes, de la antigua Grecia, fue uno de los primeros seres humanos que calculó Pi, probablemente ayudando a los fabricantes de ruedas. Pero, ¿cómo calculó el valor de pi?

En primer lugar, vio que todos los polígonos como un círculo. Según Arquímedes, si se sigue aumentando el número de los lados de un polígono, se acercaría al círculo perfecto. En otras palabras, un pentágono es más círculo que un cuadrado, pero un hexágono es más círculo que un pentágono, y así sucesivamente… Así, el legendario matemático Arquímedes definió un círculo como un polígono regular con un número extremadamente grande de lados hace más de dos mil años.

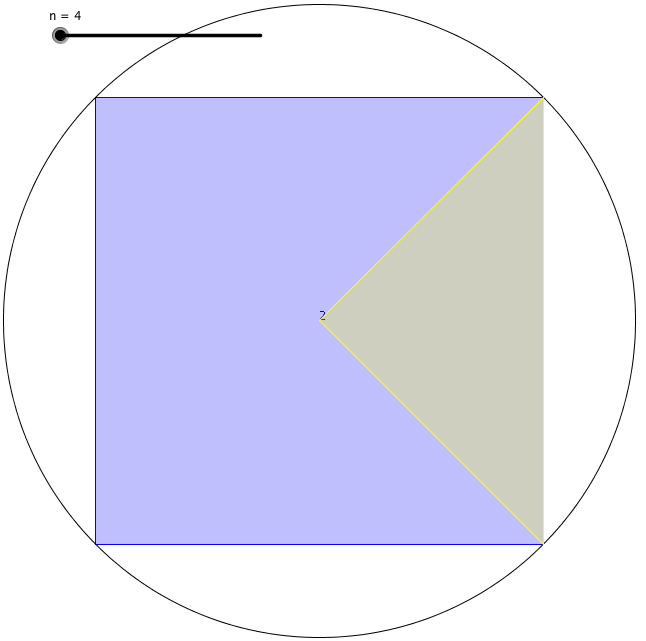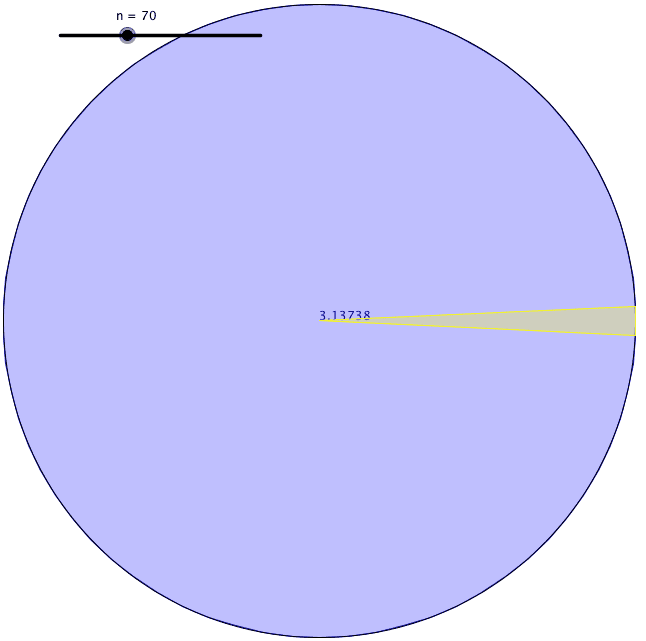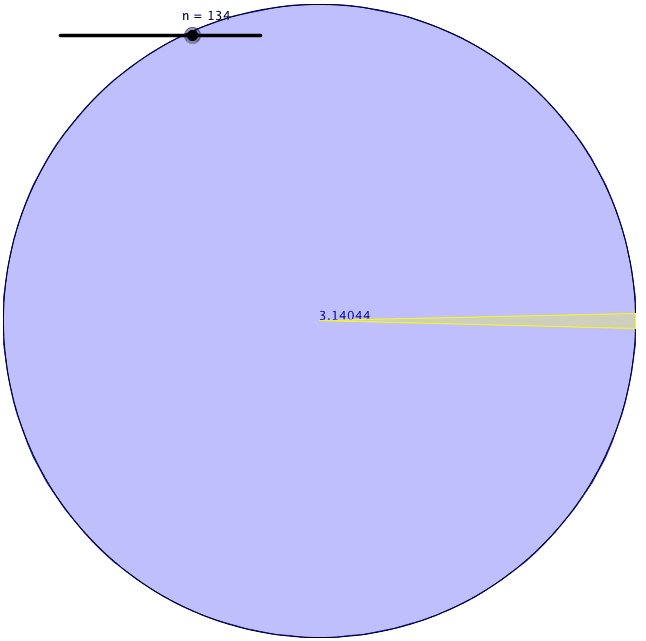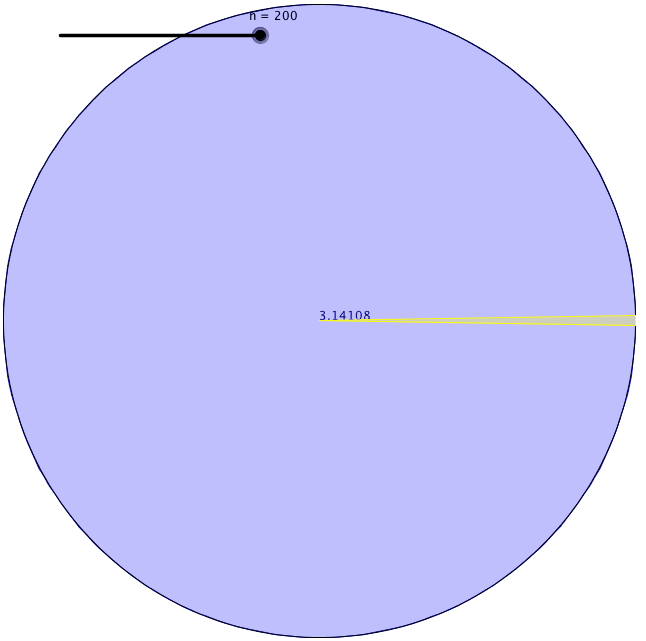
Su definición es útil porque medir una superficie curva era difícil de hacer con precisión. Encontró una manera de encontrar la circunferencia de un círculo. Primero, dibujó un cuadrado con sus esquinas tocando el perímetro de un círculo y encontró el perímetro del cuadrado inscrito. En segundo lugar, dibujó otro cuadrado con sus lados tocando también el perímetro del círculo y halló el perímetro del cuadrado circunscrito. Llegó a la conclusión de que la circunferencia del círculo tenía que estar en algún lugar entre el valor de esos dos perímetros de los cuadrados.

Usando este método, sin embargo, la diferencia entre esos dos valores era bastante grande cuando usaba cuadrados. Así que dibujó pentágonos para ver los límites superior e inferior de la circunferencia del círculo. En ese momento obtuvo un rango menor de límites. Después, siguió aumentando el número de caras del polígono que dibujaba dentro y fuera del círculo. Cada vez que lo hacía, su estimación era más precisa. Arquímedes llegó a un polígono regular de 96 caras hasta que se agotó. El límite inferior y superior que encontró esa vez fueron 3,1408 y 3,1429. Así, calculó π con dos decimales.

El método de Arquímedes necesitaba ser mejorado porque su vida no iba a ser lo suficientemente larga como para encontrar los otros dígitos de pi a mano. Los matemáticos necesitaban descubrir fórmulas más eficientes y nuevas técnicas.

Antes de poder hacer esto, necesitaban descubrir el Álgebra. Al principio, la gente utilizaba signos para los dígitos. Por ejemplo, digamos que usted y su vecino tienen 75 caballos juntos y usted tiene 35 caballos. Necesitas encontrar el número de caballos que tiene tu vecino. Sin el álgebra, la solución llevaría mucho tiempo. Pero tras el descubrimiento del álgebra, simplemente utilizamos ecuaciones para resolver los problemas. En este ejemplo concreto, podemos escribir 75 = x + 35, donde x son los caballos de tu vecino. Escribir una ecuación de este tipo y utilizar una variable en lugar de un número fue revolucionario para el mundo clásico. El álgebra permitió realizar cálculos mucho más fáciles en todas las matemáticas.

La adopción del álgebra por parte de los grandes matemáticos inspiró toda una nueva forma de ver el mundo. El siguiente gran salto en el cálculo de pi fue la invención del cálculo. Después de eso, los matemáticos comenzaron a trabajar en series infinitas. Una serie infinita es una expresión con números que se suman uno tras otro hasta el infinito, y a veces estas series infinitas convergen a un valor particular.

Ahora hay muchos métodos disponibles para calcular Pi. Gottfried Leibniz encontró pi en el infinito. James Gregory encontró la ecuación siguiente para pi. Estaba trabajando en una de las asombrosas series infinitas para la función tangente inversa de abajo. Sumó infinitamente muchos números pequeños y encontró pi.

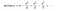
Puso x = 1 en la serie tangente inversa.serie tangente. Nos mostró que cuanto más lejos vayamos, más cerca de la estimación de pi estaremos. Sin embargo, para obtener 10 dígitos de pi, necesitamos escribir unos 5 mil millones de fracciones para sumar.