La prueba F para el análisis de regresión

Un procedimiento paso a paso para utilizar la prueba F

Para lograr los objetivos anteriores, seguiremos estos pasos:

1. Formule el estadístico de prueba para la prueba F, también conocido como el estadístico F.
2. Identificar la Función de Densidad de Probabilidad de la variable aleatoria que representa el estadístico F bajo el supuesto de que la hipótesis nula es verdadera.
3. Introducir los valores en la fórmula del estadístico F y calcular el valor de probabilidad correspondiente utilizando la Función de Densidad de Probabilidad encontrada en el paso 2. Esta es la probabilidad de observar el valor del estadístico F suponiendo que la hipótesis nula es verdadera.
4. Si la probabilidad encontrada en el paso 3 es menor que el umbral de error, como 0,05, rechace la hipótesis nula y acepte la hipótesis alternativa con un nivel de confianza de (1,0 – umbral de error), por ejemplo, 1-0,05 = 0,95 (es decir, un nivel de confianza del 95%). En caso contrario, acepte la hipótesis nula con una probabilidad de error igual al umbral de error, por ejemplo, al 0,05 o al 5%.
Sumérjase en estos pasos.

PASO 1: Desarrollar la intuición para el estadístico de prueba

Recuerde que la prueba F mide cuánto mejor es un modelo complejo en comparación con una versión más simple del mismo modelo en su capacidad para explicar la varianza de la variable dependiente.

Considere dos modelos de regresión 1 y 2:

• Sea que el modelo 1 tiene k_1 parámetros. El modelo 2 tiene parámetros k_2.
• Déjese k_1 < k_2
• Así, el modelo 1 es la versión más simple del modelo 2. es decir, el modelo 1 es el modelo restringido y el modelo 2 es el modelo no restringido. El modelo 1 puede anidarse dentro del modelo 2.
• Déjese que RSS_1 y RSS_2 sean la suma de cuadrados de los errores residuales después de que el modelo 1 y el modelo 2 se ajusten al mismo conjunto de datos.
• Déjese que n sea el número de muestras de datos.

Con las definiciones anteriores, el estadístico de prueba de la prueba F para la regresión puede expresarse como una razón de la siguiente manera:



La fórmula del estadístico F permite calcular qué parte de la varianza de la variable dependiente el modelo más simple no es capaz de explicar en comparación con el modelo complejo, expresado como una fracción de la varianza no explicada del modelo complejo.

En el análisis de regresión, el error cuadrático medio del modelo ajustado es una excelente medida de la varianza no explicada. Lo que explica los términos RSS en el numerador y el denominador.

El numerador y el denominador se escalan adecuadamente utilizando los correspondientes grados de libertad disponibles.

El estadístico F es en sí mismo una variable aleatoria.

Determinemos a qué función de densidad de probabilidad obedece el estadístico F.

PASO 2: Identificación de la función de densidad de probabilidad del estadístico F

Note que tanto el numerador como el denominador del estadístico de prueba contienen sumas de cuadrados de errores residuales. Recuerde también que en la regresión, un error residual resulta ser una variable aleatoria con alguna función de densidad de probabilidad (o de masa de probabilidad), es decir, una FDP o FPM dependiendo de si es continua o discreta. En este caso lo que nos interesa es encontrar la PDF del estadístico F.

Si suponemos que los errores residuales de los dos modelos son 1) independientes y 2) se distribuyen normalmente, que por cierto resultan ser requisitos de la regresión por mínimos cuadrados ordinarios, entonces se puede ver que el numerador y el denominador de la fórmula del estadístico F contienen sumas de cuadrados de variables aleatorias independientes y normalmente distribuidas.

Se puede demostrar que la suma de cuadrados de k variables aleatorias independientes y normales sigue la PDF de la distribución Chi-cuadrado(k).



Así, el numerador y el denominador de la fórmula del estadístico F pueden mostrarse obedeciendo cada uno a versiones escaladas de dos distribuciones Chi-Cuadrado.

Con un poco de matemáticas, también se puede demostrar que el cociente de dos variables aleatorias con distribución chi-cuadrado convenientemente escalada es en sí mismo una variable aleatoria que sigue la distribución F, cuya PDF se muestra a continuación.



En otras palabras:

Si la variable aleatoria X tiene la PDF de la distribución F con parámetros d_1 y d_2, es decir :



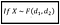
Entonces, se puede demostrar que X se expresa como el cociente de dos variables aleatorias convenientemente escaladas X_1 y X_2, cada una de las cuales tiene la PDF de una distribución Chi-cuadrado. Es decir :



Ahora recuerde que k_1 y k_2 son el número de variables en los modelos simples y complejos M1 y M2 introducidos anteriormente, y n es el número de muestras de datos.

Sustituir d_1 y d_2 como sigue:

d_1 = (k_2 – k_1) que es la diferencia de grados de libertad de los residuos de los dos modelos M1 y M2 a comparar, y

d_2 = (n – k_2) que son los grados de libertad de los residuos del modelo complejo M2,

Con estas sustituciones, podemos reescribir la fórmula de la distribución F de la siguiente manera:



Comparemos la fórmula anterior con la fórmula del estadístico F (reproducida a continuación), donde sabemos que el numerador y el denominador contienen PDFs convenientemente escaladas de las distribuciones Chi-cuadrado:



Comparando estas dos fórmulas, está claro que:

1. El grado de libertad ‘a’ de la distribución Chi-cuadrado en el numerador es (k1 – k2).
2. El grado de libertad ‘b’ de la distribución Chi-cuadrado en el denominador es (n – k2).
3. El estadístico de prueba de la prueba F tiene la misma PDF que la de la distribución F.

En otras palabras, el estadístico F sigue la distribución F.

Paso 3: Calcular el valor del estadístico F

Si utiliza el estimador OLS de statsmodels, este paso es una operación de una sola línea. Todo lo que tiene que hacer es imprimir OLSResults.summary() y obtendrá:

1. El valor del estadístico F y,
2. El valor ‘p’ correspondiente, es decir, la probabilidad de encontrar este valor, a partir de la PDF de la distribución F.

La biblioteca statsmodels hará el trabajo sucio de ambos cálculos.

print(ols_results.summary())

Esto imprime lo siguiente:



Paso 4: Determinar si la hipótesis nula puede ser aceptada

Dado que OLSResults.summary() imprime la probabilidad de ocurrencia del estadístico F bajo el supuesto de que la hipótesis nula es verdadera, sólo necesitamos comparar esta probabilidad con nuestro valor umbral alfa. En nuestro ejemplo, el valor p devuelto por .summary() es 4,84E-16, que es un número excesivamente pequeño. Mucho más pequeño que incluso alfa = 0,01. Por lo tanto, hay mucho menos del 1% de probabilidad de que el estadístico F de 136,7 pueda haber ocurrido por casualidad bajo el supuesto de una hipótesis nula válida.

Por lo tanto, rechazamos la hipótesis nula y aceptamos la hipótesis alternativa H_1 de que el modelo complejo, es decir, el modelo de variable retardada, a pesar de sus defectos obvios, es capaz de explicar la varianza en la variable dependiente Precio de cierre mejor que el modelo de sólo intercepción.