¿El decaimiento causa el olvido? En el caso de la memoria a largo plazo, la respuesta suele ser «no» (por ejemplo, McGeoch, 1932). Sin embargo, en el caso de la memoria a corto plazo, el debate continúa (por ejemplo, Altmann y Gray, 2008; Lewandowsky et al., 2009). La cuestión tiene importantes implicaciones teóricas, ya que la afirmación de que el olvido difiere a lo largo de las escalas de tiempo es fundamental para los argumentos contra los modelos de memoria que niegan la utilidad de distinguir entre la memoria a corto y a largo plazo (por ejemplo, Brown et al., 2007). Aquí abordamos dos cuestiones pendientes. La primera se refiere a los datos empíricos. Aunque muchos resultados tomados como evidencia de la decadencia han sido explicados por cuentas alternativas (por ejemplo, en términos de interferencia: Neath y Brown, 2006; Brown et al., 2007), se ha argumentado que el olvido demostrado por Baddeley y Scott (1971) no puede explicarse sin recurrir a la decadencia de rastros. De hecho, Nairne (2003, p. 429) afirmó que «las conclusiones a las que llegaron Baddeley y Scott (1971) han dominado ampliamente el campo durante las últimas tres décadas». Aquí argumentamos que una explicación basada en la interferencia, originalmente descartada por Baddeley y Scott, puede de hecho dar cuenta de sus datos. La segunda cuestión es conceptual, y se refiere a la posible equivalencia de los modelos de memoria decaída y no decaída.
Los hallazgos de Baddeley y Scott (1971)
En una tarea típica de Brown-Peterson (Brown, 1958; Peterson y Peterson, 1959), los sujetos ven tres elementos (normalmente consonantes) y, después de un retraso de 3 a 30 s, intentan recordarlos en orden. Se impide el ensayo durante la retención y se produce el olvido a lo largo del tiempo. Sin embargo, Keppel y Underwood (1962) no observaron ninguna diferencia en el rendimiento en las distintas condiciones de retraso en el primer ensayo de una tarea Brown-Peterson. Por ejemplo, en su Experimento 2, el rendimiento en el primer ensayo fue idéntico independientemente de si el periodo distractor duraba 3, 9 o 18 s (para una revisión, véase Surprenant y Neath, 2009a). Llegaron a la conclusión de que la interferencia, y no el decaimiento del rastro, era la responsable del olvido a corto plazo. En consonancia con el punto de vista de la interferencia, el rendimiento disminuyó a lo largo de los ensayos.
Baddeley y Scott (1971), sin embargo, sugirieron que los datos de Keppel y Underwood (1962) sufrían efectos techo que podrían haber enmascarado el olvido. Por lo tanto, abordaron el olvido en el primer ensayo cuando los efectos de techo estaban ausentes. En el Experimento 1, 152 sujetos escucharon una única lista de dígitos de cinco elementos en orden aleatorio que recordaron después de 3, 30, 60 o 120 s. Durante el retraso, los sujetos escribieron letras que fueron leídas en voz alta por el experimentador. Los resultados (puntos de datos, panel izquierdo de la Figura 1) incluían una clara evidencia de olvido entre 3 y 30 s en el primer (es decir, único) ensayo.
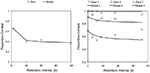
Figura 1. Los puntos de datos muestran la proporción de ítems recordados correctamente en el Experimento 1 de Baddeley y Scott (1971) (panel izquierdo) y la proporción de ítems recordados correctamente de listas de tres, cinco y siete ítems en el Experimento 2 (panel derecho) en función del retraso. Las líneas continuas muestran el ajuste de SIMPLE (véase el texto para más detalles).
El Experimento 2 siguió explorando el olvido en un solo ensayo. Cuatrocientos veinticuatro sujetos recordaron listas de dígitos de tres, cinco o siete elementos después de 0, 3, 6, 9, 18 o 36 s. La tarea distractora fue de nuevo escribir letras. Los resultados se muestran (como puntos de datos) en el panel derecho de la Figura 1. Baddeley y Scott(1971, p. 282) incluyeron en su análisis datos de otros estudios y observaron que en todos los estudios, incluido el suyo, «el olvido se aproxima a la asíntota en aproximadamente 5 s». Se consideraron y descartaron otras posibles fuentes de interferencia. En primer lugar, se consideró improbable la interferencia retroactiva de la tarea distractora debido a la falta de pruebas de que las letras y los dígitos se interfieran mutuamente (Wickens et al., 1963). En segundo lugar, se descartó la interferencia dentro de la secuencia (elementos de la lista que interfieren entre sí) porque dicha interferencia debería conducir a un olvido más rápido de las listas más largas (véase Melton, 1963) y esto no se observó. Baddeley y Scott (1971), por lo tanto, tomaron sus resultados como evidencia de un componente de memoria primaria que decae en unos 5 s. Desde su publicación, el estudio se ha citado ampliamente como evidencia en contra de una cuenta de interferencia de los datos y como evidencia de la decadencia; hay pocas cuentas alternativas de estos datos particulares y ningún intento sistemático de modelar los datos1. ¿Puede un modelo sin decadencia de rastros explicar los datos? Aquí aplicamos un modelo de distinción temporal, memoria, percepción y aprendizaje independientes de la escala (SIMPLE; Neath y Brown, 2006; Brown et al, 2007), a los resultados reportados por Baddeley y Scott.
Evidencia para la interferencia
SIMPLE – memoria, percepción y aprendizaje independientes de la escala se ha descrito en detalle en otros lugares (por ejemplo, Neath y Brown, 2006; Brown et al., 2007); aquí, nos centramos en aquellos aspectos relevantes para la simulación actual. La memoria se concibe como una tarea de discriminación: los elementos se representan como ubicaciones a lo largo de una o más dimensiones en el espacio psicológico y, en general, aquellos elementos con menos vecinos cercanos en las dimensiones relevantes en el momento de la recuperación tendrán más probabilidades de ser recordados que los elementos con más vecinos cercanos. Según SIMPLE, los ítems no relacionados en las tareas de memoria episódica se representan principalmente o únicamente a lo largo de una dimensión temporal2. El punto cero es el momento en que se recupera el ítem, y el valor de cada ítem es el tiempo transcurrido desde la presentación, en relación con el momento de la recuperación.
En el experimento 1 de Baddeley y Scott (1971), la tasa de presentación fue de un ítem por segundo, y por tanto, los valores temporales iniciales al final de la presentación serán 5, 4, 3, 2 y 1 para los ítems 1-5, respectivamente. A estos valores se añade la duración del intervalo de retención (3, 30, 60 o 120 s, según la condición). Se supone que el recuerdo lleva tiempo; asumimos que cada ítem tarda 1 s en ser recordado. Los valores resultantes se transforman logarítmicamente, y la probabilidad de recuerdo de un elemento concreto depende de su distintividad local.
La similitud, ηi,j, entre dos representaciones de memoria temporal transformadas logarítmicamente, LTi y LTj, viene dada por la Ec. 1:

El principal parámetro libre en SIMPLE es c: los valores más altos de c corresponden a una mayor distintividad y, por tanto, a una menor influencia de los elementos más distantes.
La discriminabilidad del ítem i, Di, cuando se le da la pista (ubicación temporal) para el estímulo j, Cj, viene dada por la Ec. 2, en la que n es el número de ítems del conjunto:
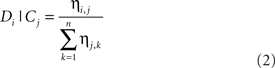
Los errores de admisión son posibles a través de la Ec. 3, que muestra la probabilidad de recuerdo, Ri, en función de la discriminabilidad:

El parámetro t es el umbral y el parámetro s puede interpretarse como el ruido del umbral. Lo anterior es la misma forma en que SIMPLE se ha aplicado a los datos de recuerdo de serie en demostraciones anteriores (véase Neath y Brown, 2006; Brown et al., 2007).
Hay, pues, tres parámetros libres. Con c = 3,248, s = 8,253 y t = 0,269, SIMPLE muestra un claro olvido (las líneas del panel izquierdo de la Figura 1) y produce adecuadamente el mismo patrón observado por Baddeley y Scott (1971) en su Experimento 1 (R2 = 0,954). Por lo tanto, a pesar de no incorporar el decaimiento de las trazas, SIMPLE da cuenta de los datos del Experimento 1 de Baddeley y Scott exactamente de la misma manera que lo hace para el recuerdo inmediato en serie en general.
¿Por qué el rendimiento en el modelo disminuye entre 3 y 30 s, pero luego efectivamente se asimila? La clave es lo que Brown et al. (2007) denominan compresión weberiana. Los valores temporales originales sufren una transformación logarítmica, que condensa más los valores grandes que los pequeños. Por lo tanto, hay menos diferencia al comparar la distintividad de los ítems tras un retraso de 30 y 60 s que al comparar la distintividad de los ítems tras un retraso de 0 y 30 s.
Se siguió el mismo procedimiento básico para ajustar los datos del Experimento 2 de Baddeley y Scott (1971). Los parámetros se fijaron en c = 0,547, s = 23,131 y t = 0,139 para las tres longitudes de lista y los seis retrasos. Los resultados se muestran como líneas en el panel derecho de la Figura 1 (R2 = 0,937). El olvido diferencial entre las listas de tres, cinco y siete ítems se explica completamente por la presencia de ítems adicionales en la lista, lo que se denomina interferencia intrasequencia.
Discusión
La explicación dominante de los datos de Baddeley y Scott (1971) es que ofrece apoyo a una explicación multisistémica de la memoria en la que la memoria primaria (o a corto plazo o de trabajo) decae en unos pocos segundos y el recuerdo a más largo plazo se apoya en un segundo sistema de memoria (véase Nairne, 2003). La lógica subyacente era que, dado que todas las fuentes de interferencia se minimizaban o eliminaban, cualquier olvido observado debía deberse al decaimiento.
Baddeley y Scott (1971) descartaron la interferencia intrasequencia como explicación porque se centraron en el relato de Melton (1963) sobre la interferencia intrasequencia, que efectivamente predice un olvido más rápido para las listas más largas. Por el contrario, SIMPLE no hace esta predicción porque es un modelo de distinción local: la cantidad de interferencia para un elemento dado se ve más afectada por los vecinos cercanos y, por lo tanto, ampliar la longitud de la lista no garantiza necesariamente un olvido más rápido. Por lo tanto, es posible explicar los datos reportados por Baddeley y Scott sin invocar ni el decaimiento ni dos sistemas de memoria separados, y en su lugar, invocando la misma cuenta de interferencia utilizada para explicar los datos de otros paradigmas (véase Surprenant y Neath, 2009b).
¿Equivalencia entre los modelos de decaimiento y de interferencia?
Hemos demostrado que un modelo sin decaimiento acomoda los resultados empíricos que durante mucho tiempo se han tomado como evidencia para el decaimiento. Podría argumentarse, sin embargo, que el modelo SIMPLE puede interpretarse como un modelo de alto nivel que no especifica los procesos clave subyacentes (es decir, decaimiento frente a interferencia)3. Esencialmente, esta acusación argumenta que el concepto de «distinción relativa», que es fundamental para el comportamiento de SIMPLE, podría implementarse a través de mecanismos de decaimiento de rastros. Consideramos esto dentro del contexto de un modelo de decaimiento basado en el tiempo de Anderson et al. (1998), que utiliza el marco de ACT-R.
En el modelo ABLM, la activación de línea base de una sola ocurrencia de un chunk en la memoria decae como una función logarítmica del tiempo transcurrido. Por lo tanto, las activaciones de la línea de base de los ítems están en las mismas relaciones entre sí que las distancias temporales transformadas logarítmicamente utilizadas por SIMPLE y podrían, al menos algebraicamente, ser utilizadas para el mismo propósito, de la misma manera que las dimensiones distintas del tiempo se han utilizado con SIMPLE (véase el capítulo 8 de Surprenant y Neath, 2009b). Específicamente, si la confusabilidad de los ítems en la memoria estuviera relacionada con las diferencias en sus niveles de activaciones basales decadentes, y la probabilidad de recordar un ítem dado estuviera inversamente relacionada con su confusabilidad sumada con todos los demás ítems, entonces se podría utilizar un mecanismo de decadencia de trazos para implementar los mismos cálculos de distintividad temporal que SIMPLE supone4.
La interpretación psicológica de este tipo de cuenta, sin embargo, parece algo contraintuitiva. La interpretación de la teoría del decaimiento afirma que lo que hace que un elemento temporalmente distante sea difícil de recordar no es su bajo nivel de activación, sino el hecho de que hay muchos otros elementos con niveles de activación igualmente bajos. De hecho, en este modelo no habría ninguna relación directa entre el nivel de activación de un ítem y la probabilidad de recordarlo; en su lugar, lo único que importaría es la similitud del nivel de activación del ítem con los niveles de activación de otros ítems. Sería poco natural, entonces, decir que el olvido se produce debido a la decadencia.
Suponemos que un mecanismo plausible de olvido basado en la decadencia hace al menos dos afirmaciones: primero, que las activaciones se reducen con el tiempo y, segundo, que la probabilidad de recuperación refleja de alguna manera el nivel absoluto de activación. Una vez que se asume que los elementos que han decaído más pueden, no obstante, recuperarse mejor, el modelo deja de ser un modelo de decaimiento de rastros en cualquier uso de sentido común. Por lo tanto, aunque la cuenta SIMPLE está redactada en un alto nivel de descripción y podría ser implementada en más de una forma, sugerimos que una interpretación en términos de decaimiento de rastros estira el significado de «decaimiento de rastros» más allá del uso normal.
En resumen, hemos argumentado que los datos clásicos de Baddeley y Scott (1971), que han sido frecuentemente tomados como evidencia de la decadencia, se explican más naturalmente en términos de distintividad temporal.
Agradecimientos
Este trabajo fue apoyado, en parte, por una subvención del NSERC a Ian Neath y por la subvención RES-062-23-2462 del Consejo de Investigación Económica y Social (Reino Unido) a Gordon D. A. Brown. El código MATLAB para las simulaciones está disponible en http://memory.psych.mun.ca/models/simple/misc/baddeley_1971.shtml o a través del primer autor.
Notas a pie de página
- ^Evans y Havens (1978) sugirieron una explicación basada en la discriminabilidad de las señales temporales, pero este trabajo no ha sido, hasta donde sabemos, citado. Henson (1998, Demostración 6) intentó ajustar su modelo Inicio-Fin a sólo la condición de siete ítems del segundo experimento de Baddeley y Scott, pero encontró que la tasa de olvido del modelo era demasiado lenta y no podía ajustarse bien a los datos.
- Notamos que existen versiones de SIMPLE en las que se utiliza una dimensión de posición, en lugar de una dimensión temporal; para una comparación directa de las dos versiones, véase Surprenant et al. (2006).
- Agradecemos a E. M. Altmann y M. P. A. Page sus sugerencias en este sentido.
- Notamos que no es así como funciona el modelo ABLM: en ese modelo la probabilidad de recordar un trozo en lugar de otro depende de la puntuación de coincidencia del trozo en relación con las puntuaciones de coincidencia de otros trozos, donde la puntuación de coincidencia depende de la similitud así como de la línea de base y otras activaciones.
Altmann, E. M., y Gray, W. D. (2008). Un modelo integrado de control cognitivo en el cambio de tarea. Psychol. Rev. 115, 602-639.
Resumen de Pubmed | Texto completo de Pubmed | Texto completo de CrossRef
Anderson, J. R., Bothell, D., Lebiere, C., y Matessa, M. (1998). Una teoría integrada de la memoria de listas. J. Mem. Lang. 38, 341.
CrossRef Full Text
Baddeley, A. D., y Scott, D. (1971). Short term forgetting in the absence of proactive interference. Q. J. Exp. Psychol. 23, 275-283.
CrossRef Full Text
Brown, G. D. A., Neath, I., y Chater, N. (2007). A temporal ratio model of memory. Psychol. Rev. 114, 539-576.
Abstracto de Pubmed | Texto completo de Pubmed | Texto completo de Cracker
Brown, J. (1958). Some tests of the decay theory of immediate memory. Q. J. Exp. Psychol. 10, 12-21.
CrossRef Full Text
Evans, T., y Havens, C. (1978). Auditory-verbal short-term-memory effects of retention interval on proactive-inhibition when interpolated interference is eliminated. Can. J. Psychol. 32, 262-269.
Abstracto de Pubmed | Texto completo de Pubmed | Texto completo de CrossRef
Henson, R. N. A. (1998). Memoria a corto plazo para el orden serial: el modelo Inicio-Fin. Cogn. Psychol. 36, 73-137.
Abstracto de Pubmed | Texto completo de Pubmed | Texto completo de CrossRef
Keppel, G., y Underwood, B. J. (1962). Proactive inhibition in short-term retention of ingle items. J. Verbal Learn. Verbal Behav. 1, 153-161.
CrossRef Full Text
Lewandowsky, S., Oberauer, K., y Brown, G. D. A. (2009). No hay decaimiento temporal en la memoria verbal a corto plazo. Trends Cogn. Sci. (Regul. Ed.) 13, 120-126.
Resumen de Pubmed | Texto completo de Pubmed | Texto completo de CrossRef
McGeoch, J. A. (1932). El olvido y la ley del desuso. Psychol. Rev. 39, 352-370.
CrossRef Full Text
Melton, A. W. (1963). Implicaciones de la memoria a corto plazo para una teoría general de la memoria. J. Verbal Learn. Verbal Behav. 2, 1-21.
CrossRef Full Text
Nairne, J. S. (2003). «Sensory and working memory», en Comprehensive Handbook of Psychology, Vol. 4: Experimental Psychology, eds A. F. Healy y R. W. Proctor (New York: Wiley), 423-444.
Peterson, L. R., y Peterson, M. G. (1959). Retención a corto plazo de ítems verbales individuales. J. Exp. Psychol. 58, 193-198.
Abstracto de Pubmed | Texto completo de Pubmed | Texto completo de CrossRef
Surprenant, A. M., y Neath, I. (2009a). «The 9 lives of short-term memory», en Interactions Between Short-Term and Long-Term Memory in the Verbal Domain, eds A. Thorn y M. Page (Hove: Psychology Press), 16-43.
Abstracto de Pubmed | Texto completo de Pubmed | Texto completo de CrossRef
Wickens, D. D., Born, D. G., y Allen, C. K. (1963). Proactive inhibition and item similarity in short-term memory. J. Verbal Learn. Verbal Behav. 2, 440-445.
CrossRef Full Text
0 comentarios