Lección 4: Multiplicar y dividir fracciones
/es/fracciones/ sumar y restar fracciones/contenido
Multiplicar fracciones
Una fracción es una parte de un entero. En la última lección, aprendiste a sumar y restar fracciones. Pero ese no es el único tipo de matemáticas que puedes hacer con las fracciones. Hay ocasiones en las que también será útil multiplicar fracciones.
Haz clic en la presentación para aprender a escribir un problema de multiplicación con fracciones.
-

Pongamos un ejemplo de multiplicación con fracciones. Supongamos que bebes 2/4 de una cafetera cada mañana.
-

Pero tu médico te acaba de decir que tienes que reducir tu consumo de café a la mitad.
-
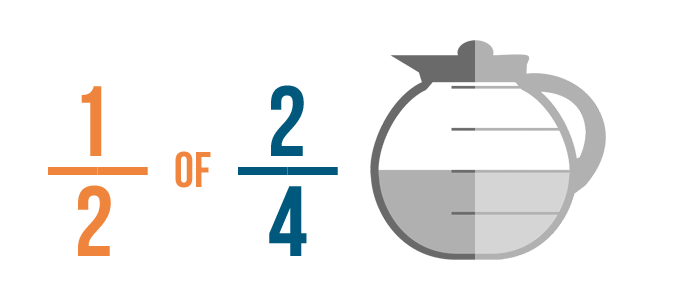
Ahora tienes que calcular cuánto es la mitad de 2/4 de una cafetera.
-
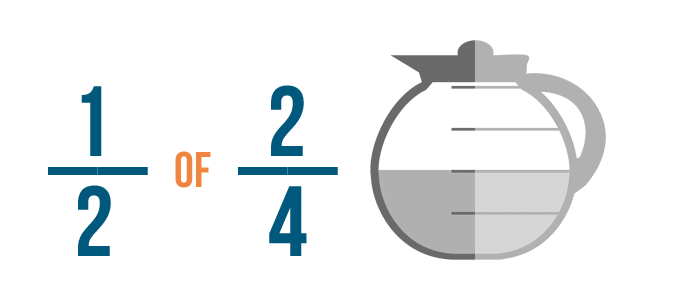
Esto puede no parecer un problema de multiplicación. Pero cuando ves la palabra de con fracciones, significa que necesitas multiplicar.
-
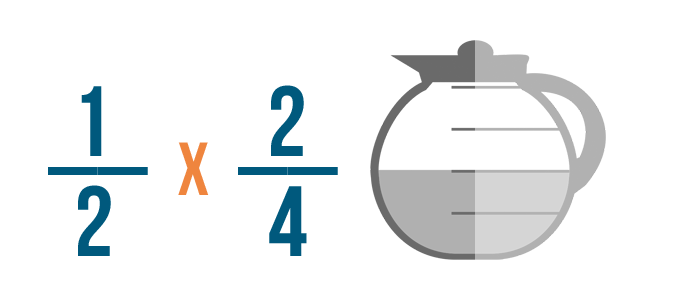
Para montar el ejemplo, simplemente sustituiremos la palabra de por un signo de multiplicación.
-
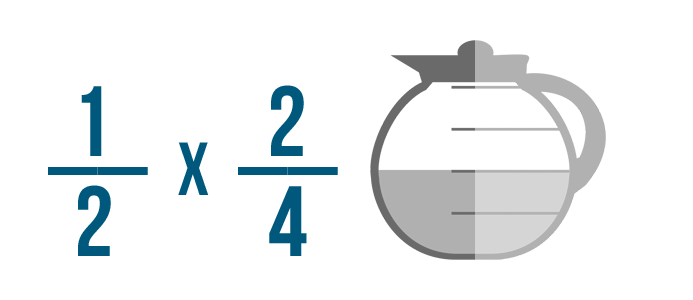
Ahora nuestro ejemplo está listo para ser resuelto.
-
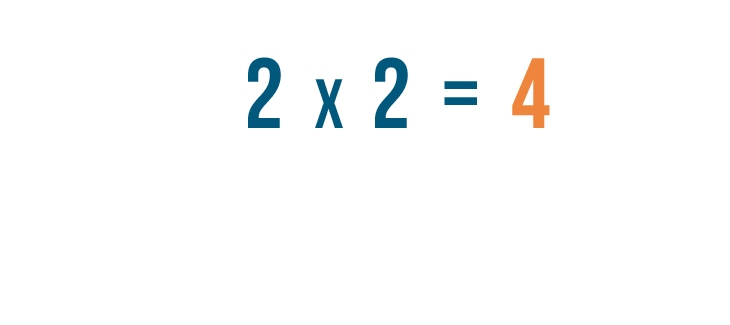
A diferencia de la multiplicación normal, que te da un número mayor…
-
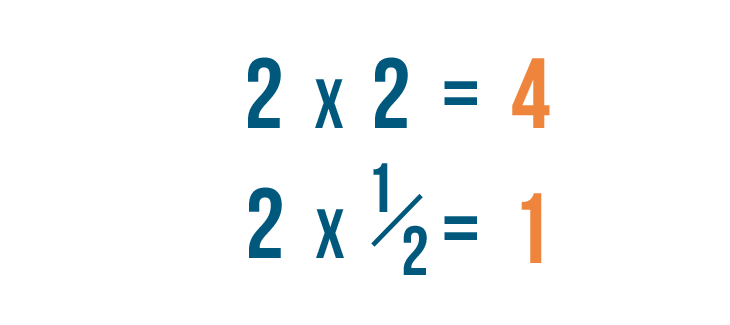
A diferencia de la multiplicación normal, que te da un número más grande…la multiplicación de fracciones normalmente te dará un número más pequeño.
-
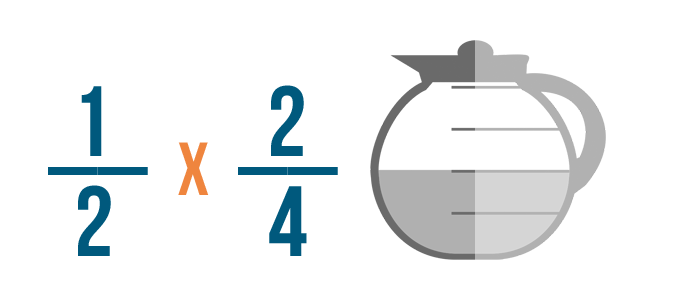
Así que cuando multiplicamos 1/2 por 2/4…
-

Así que cuando multiplicamos 1/2 por 2/4…nuestra respuesta será menor que 2/4.
-
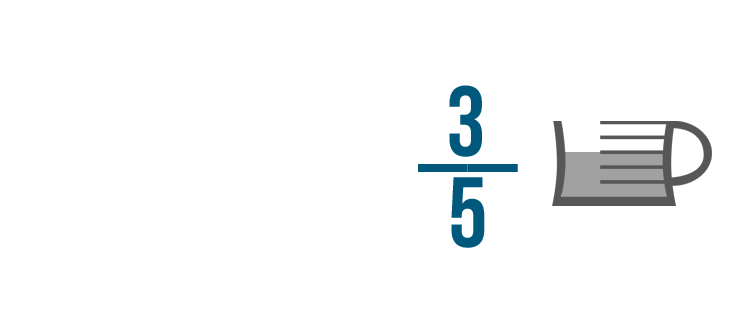
Aquí tienes otro ejemplo. Supongamos que tienes 3/5 de taza de relleno de chocolate.
-
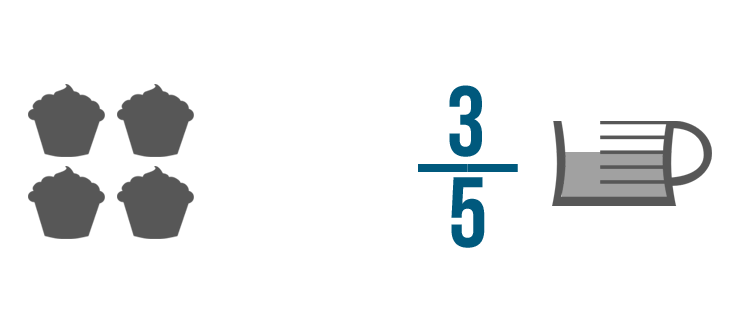
Quieres poner la misma cantidad de relleno en cada una de estas 4 magdalenas.
-
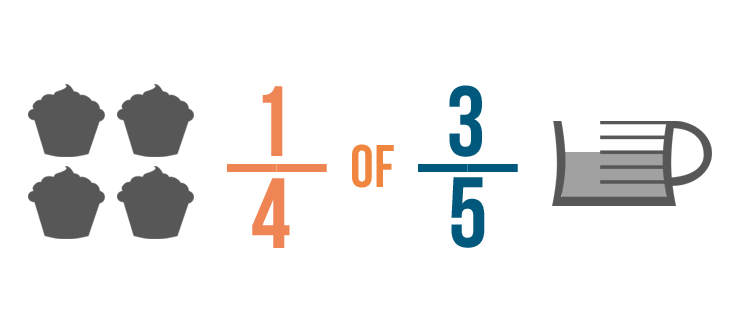
Podrías decir que quieres poner 1/4 de 3/5 de taza de relleno en cada magdalena.
-
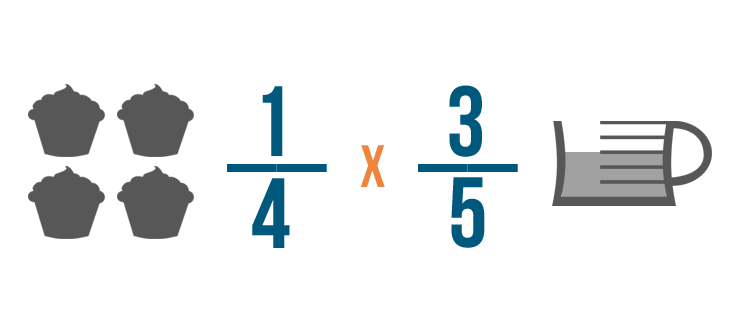
Al igual que hicimos antes, cambiaremos la palabra de por un signo de multiplicación.
-
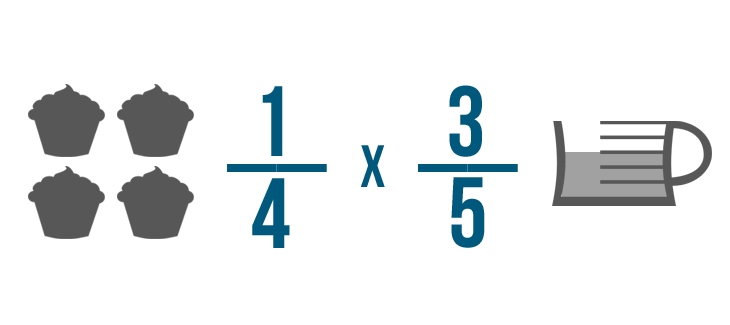
Y ahora nuestras fracciones están listas para ser multiplicadas.

¡Intenta esto!
Intenta plantear el problema de multiplicación que aparece a continuación. No te preocupes por resolverlo todavía!
Una receta pide 2/3 de taza de leche. Quieres reducir la receta a la mitad.

Nota: Aunque nuestro ejemplo dice que la respuesta correcta es 2/3 x 1/2, recuerda que con el orden de multiplicación no importa. 1/2 x 2/3 también sería correcto.
Resolución de problemas de multiplicación con fracciones
Ahora que sabemos cómo plantear problemas de multiplicación con fracciones, vamos a practicar la resolución de algunos. Si te sientes cómodo multiplicando números enteros, estás preparado para multiplicar fracciones.
Haz clic en la presentación para aprender a multiplicar dos fracciones.
-
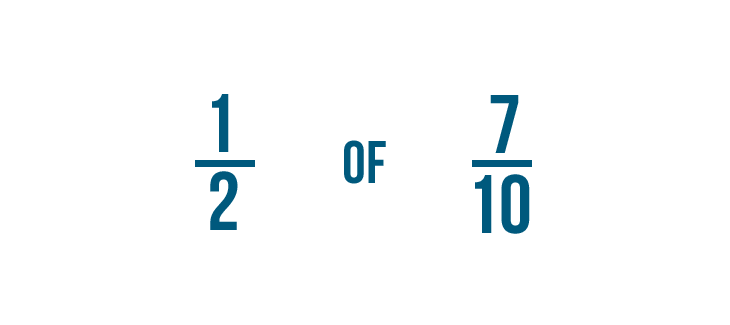
Vamos a multiplicar para encontrar 1/2 de 7/10.
-
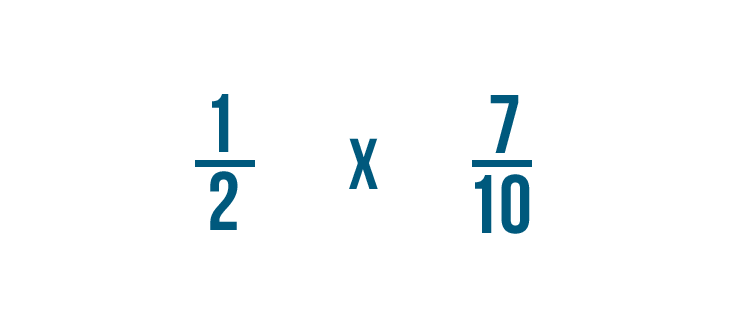
Al igual que hicimos antes, sustituiremos la palabra de por un signo de multiplicación. Ahora estamos listos para multiplicar.
-
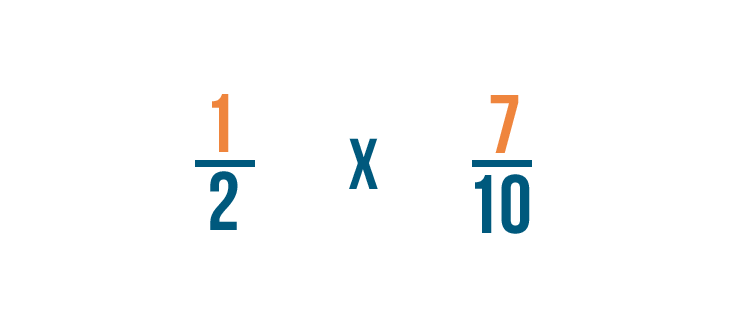
Primero, multiplicaremos los numeradores: 1 y 7.
-
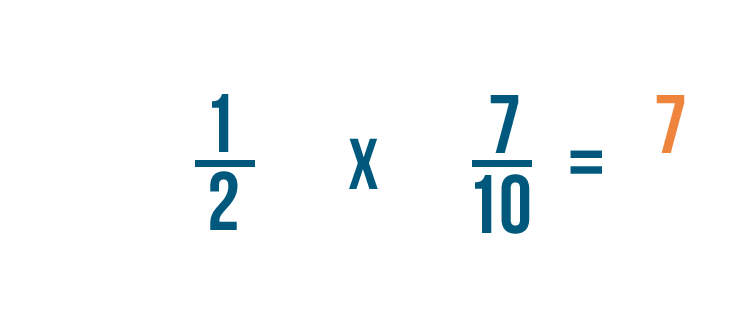
1 veces 7 es igual a 7, así que escribiremos 7 a la derecha de los numeradores.
-
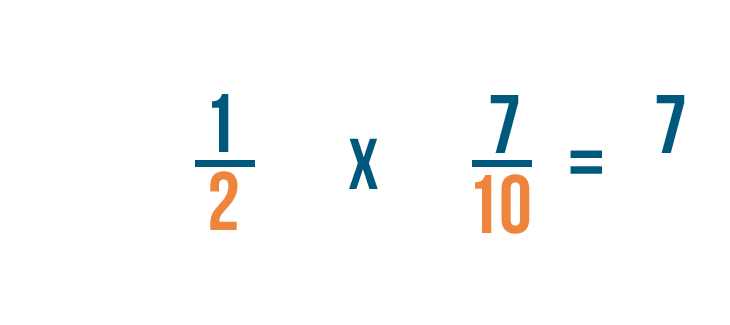
Cuando sumamos fracciones, los denominadores se quedan igual. Pero cuando multiplicamos, los denominadores también se multiplican.
-
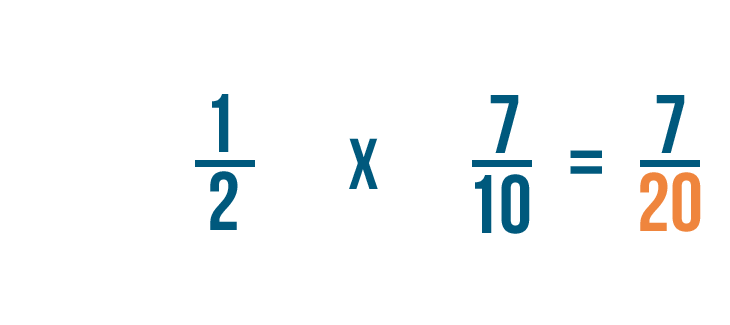
2 veces 10 es igual a 20, así que escribiremos 20 a la derecha de los denominadores.
-
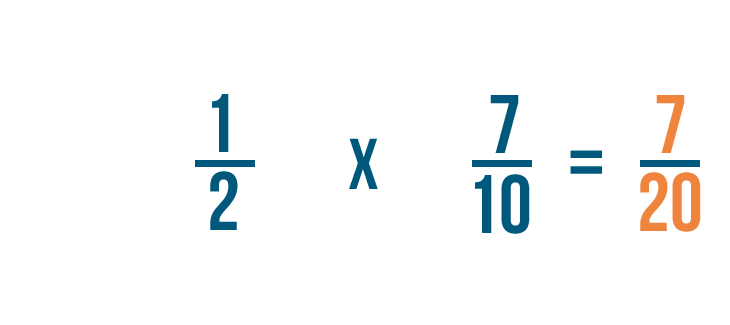
Ahora sabemos que 1/2 veces 7/10 es igual a 7/20.
-
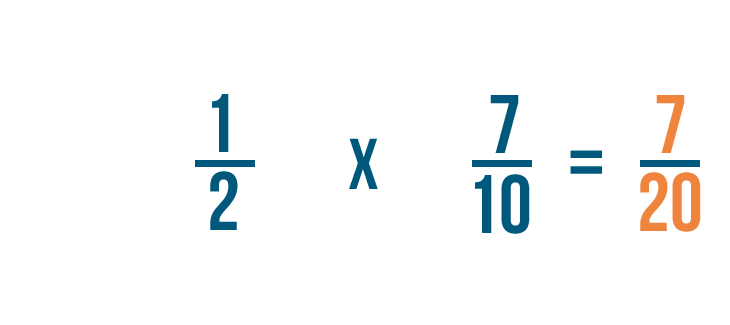
También podríamos decir que 1/2 de 7/10 es 7/20.
-
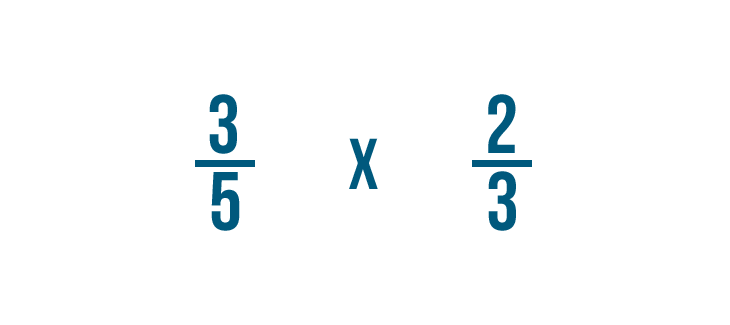
Intentemos otro ejemplo: 3/5 por 2/3.
-
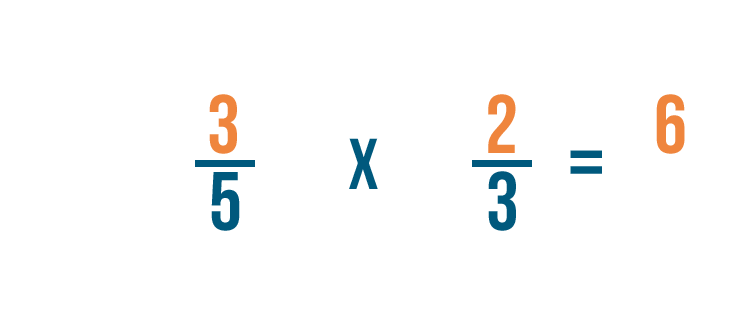
Primero, multiplicaremos nuestros numeradores. 3 por 2 es igual a 6.
-
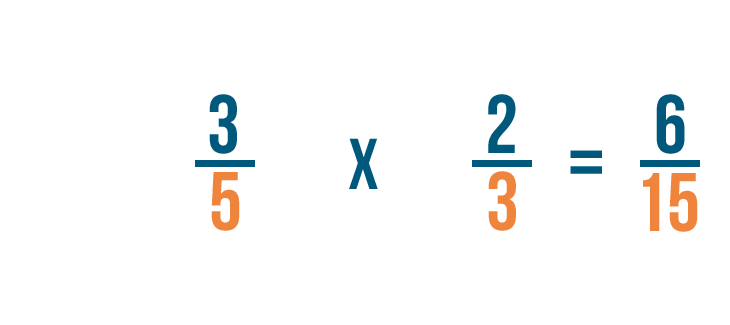
A continuación, multiplicaremos nuestros denominadores. 5 por 3 es igual a 15.
-
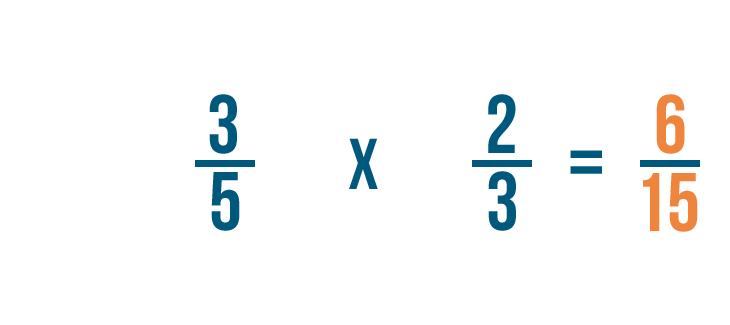
Así que 3/5 por 2/3 es igual a 6/15.

-
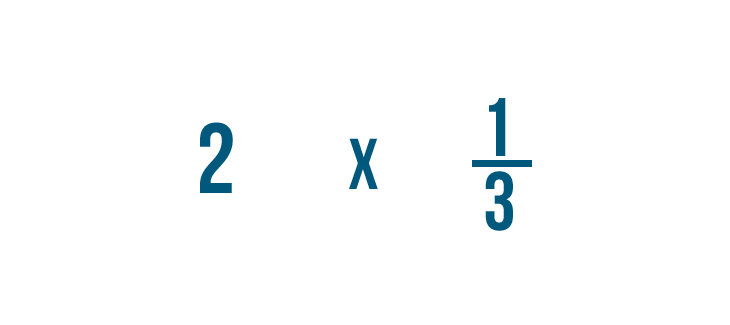
Vamos a multiplicar 2 por 1/3. Recuerda que es otra forma de preguntar: «¿Cuánto es 1/3 de 2?»
-
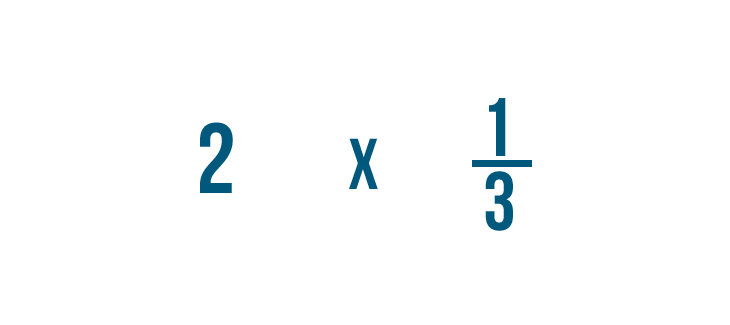
Antes de empezar, tenemos que asegurarnos de que estos números están listos para ser multiplicados.
-
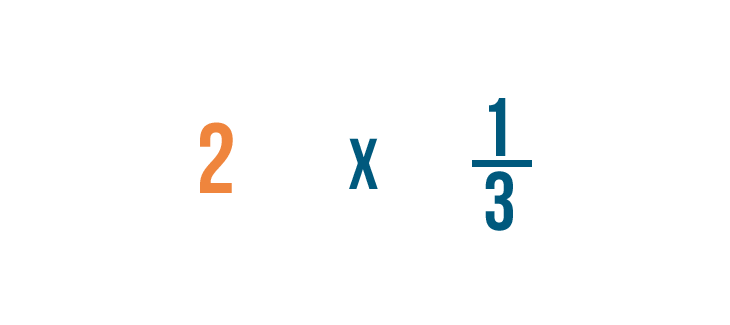
No podemos multiplicar un número entero y una fracción, así que vamos a tener que escribir 2 como fracción.
-
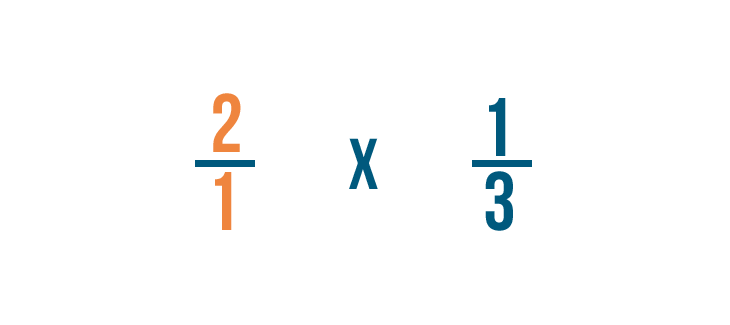
Como aprendiste en Introducción a las Fracciones, también podemos escribir 2 como 2/1.Eso es porque 2 se puede dividir por 1 dos veces.
-
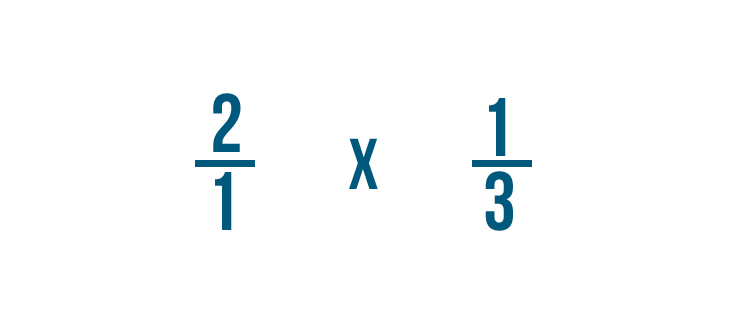
¡Ahora estamos listos para multiplicar!
-
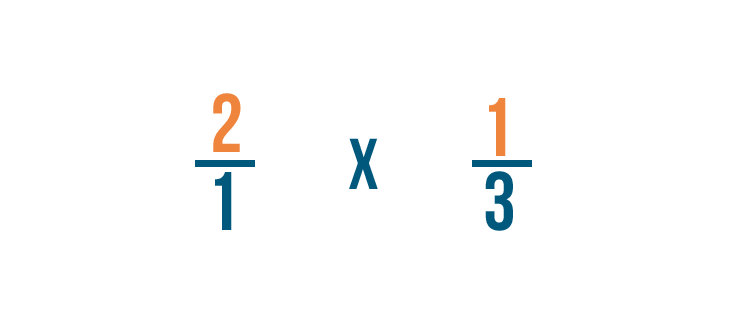
Primero, multiplicaremos los numeradores: 2 y 1.
-
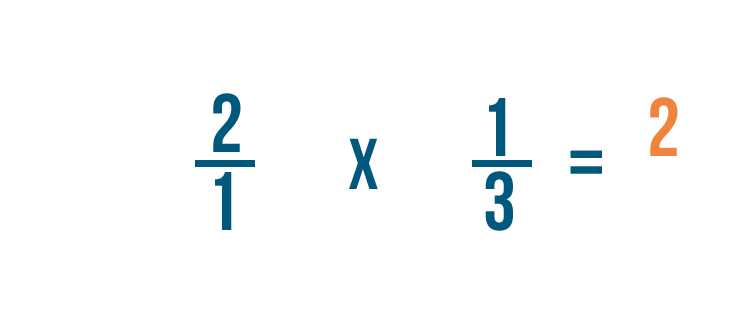
2 por 1 es igual a 2. Alinearemos el 2 con los numeradores.
-
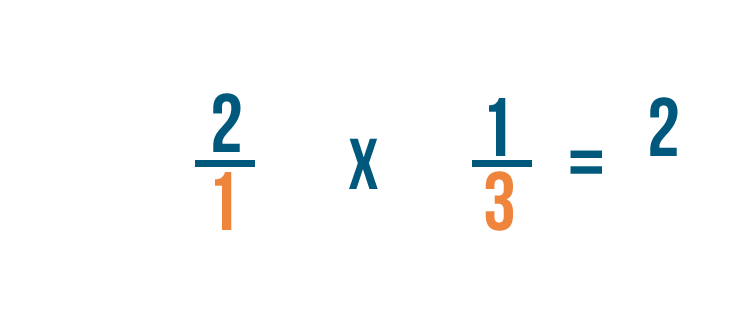
A continuación, multiplicaremos los denominadores: 1 y 3.
-
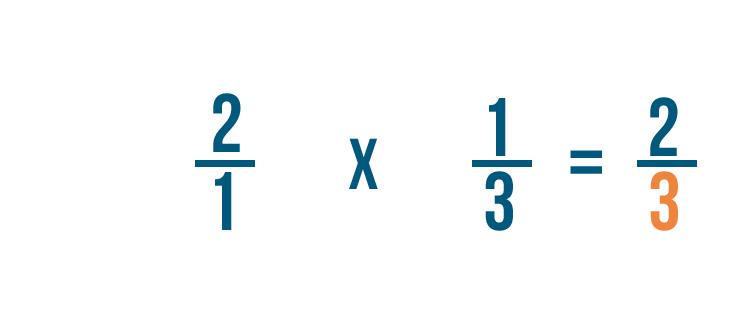
1 por 3 es igual a 3. Alinearemos el 3 con los denominadores.
-
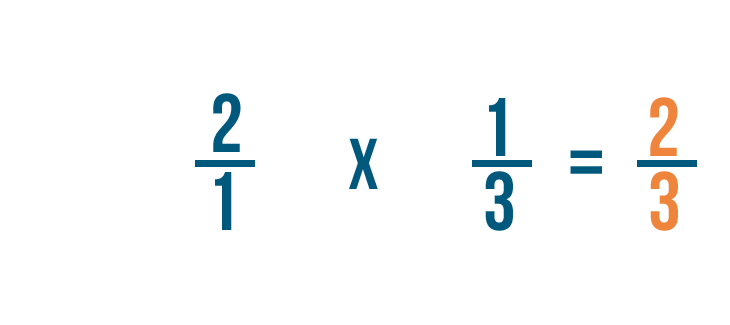
Así que 2/1 por 1/3 es igual a 2/3. También podríamos decir que 1/3 de 2 es 2/3.
-
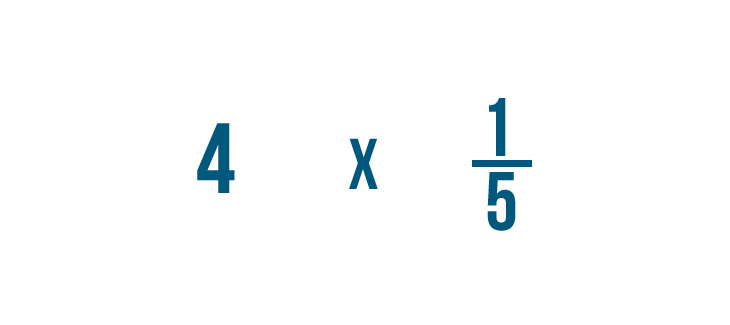
Intentemos otro ejemplo: 4 por 1/5.
-
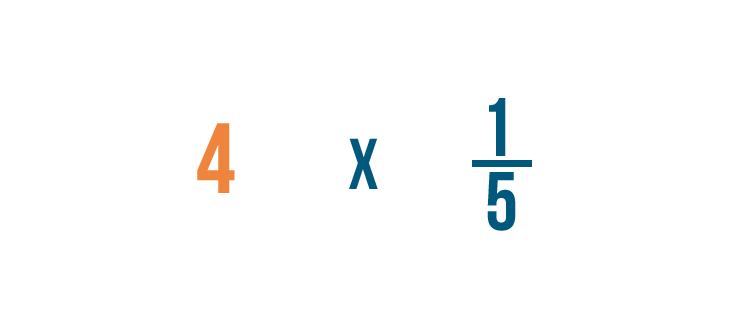
Tendremos que escribir 4 como fracción antes de empezar.
-
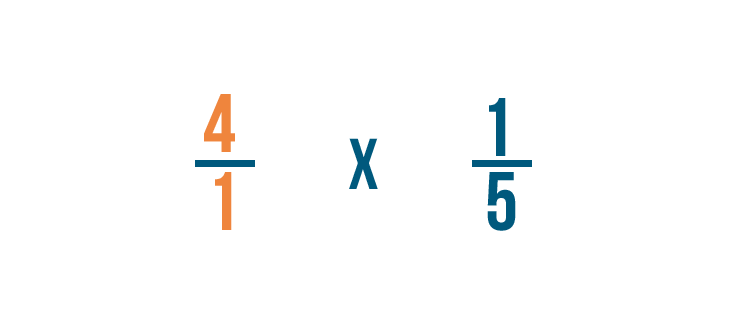
Reescribiremos 4 como 4/1. Ahora estamos listos para multiplicar.
-
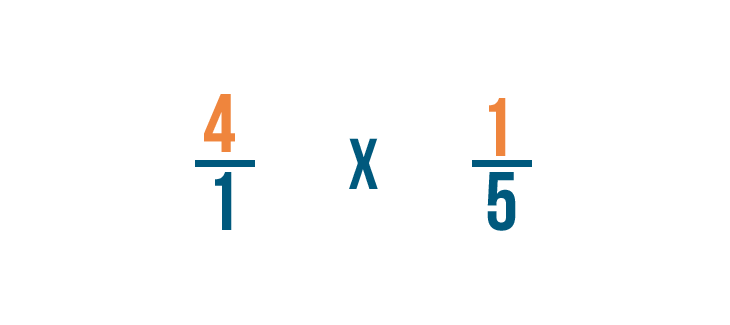
Primero, multiplicaremos los numeradores: 4 y 1.
-
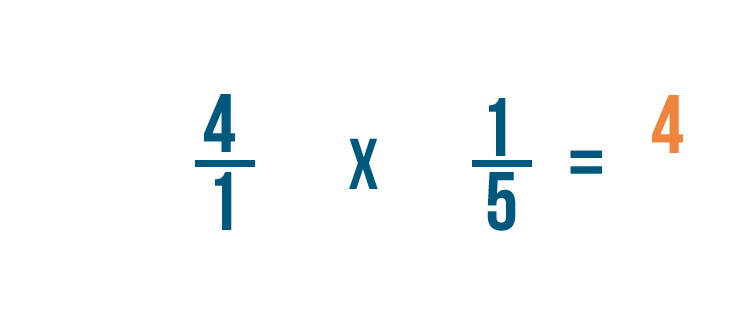
4 por 1 es igual a 4, por lo que el numerador de nuestra respuesta es 4.
-
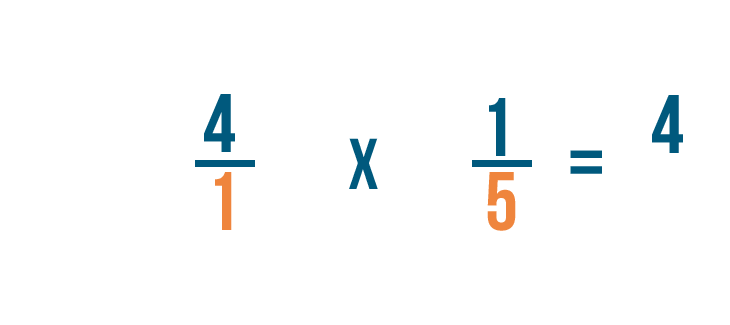
A continuación, multiplicaremos los denominadores: 1 y 5.
-
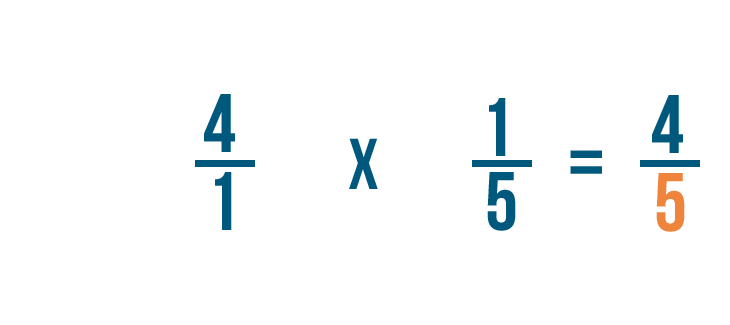
1 por 5 es igual a 5, por lo que 5 es el denominador de nuestra respuesta.
-
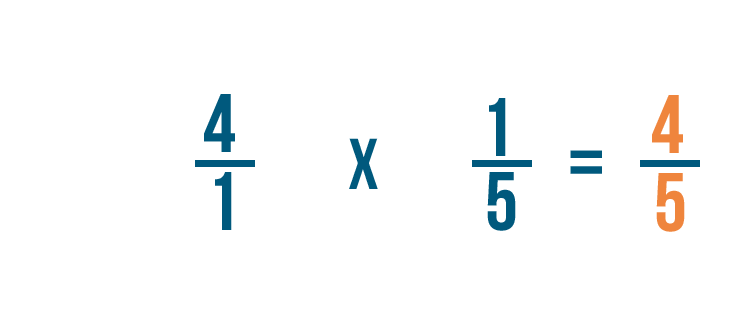
Así que 4/1 por 1/5 es igual a 4/5.

-
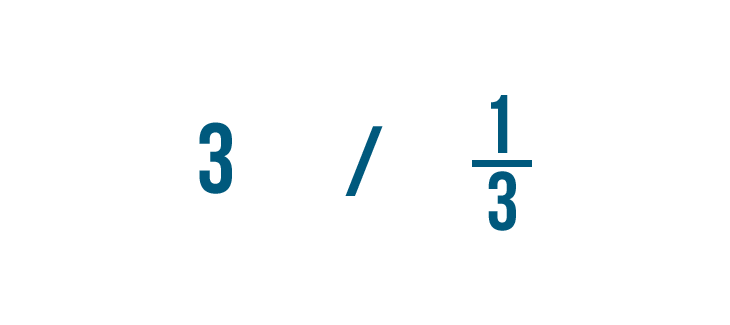
Dividamos 3 entre 1/3. Recuerda que es otra forma de preguntar «¿Cuántos tercios hay en 3?»
-
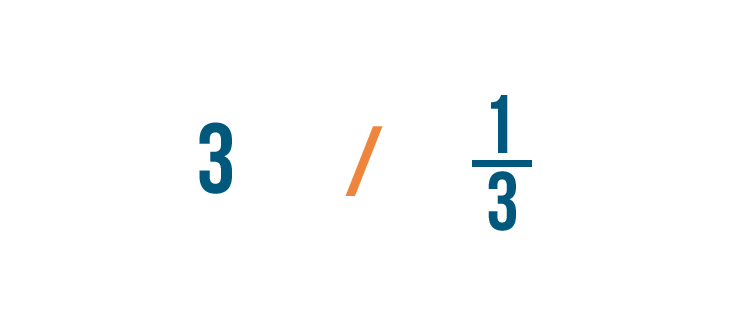
En nuestra lección sobre la división, aprendiste a escribir el signo de división así (/).
-
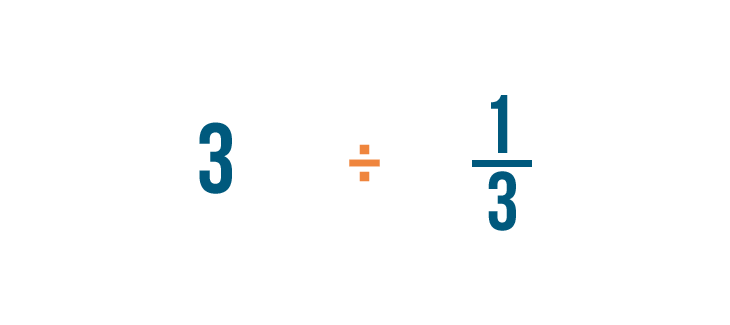
Al dividir fracciones, nos ayudará usar el otro símbolo de la división (÷) para no confundirlo con una fracción.
-
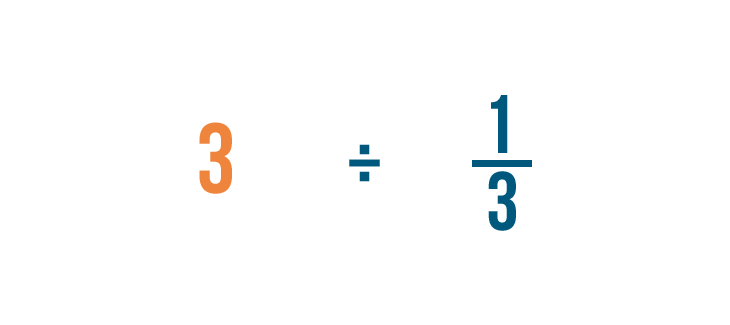
Al igual que la multiplicación, empezaremos buscando algún número entero en nuestro problema. Hay uno: 3.
-
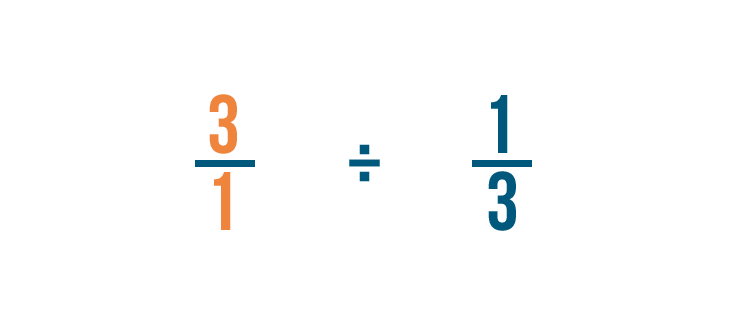
Recuerda, 3 es lo mismo que 3/1.
-
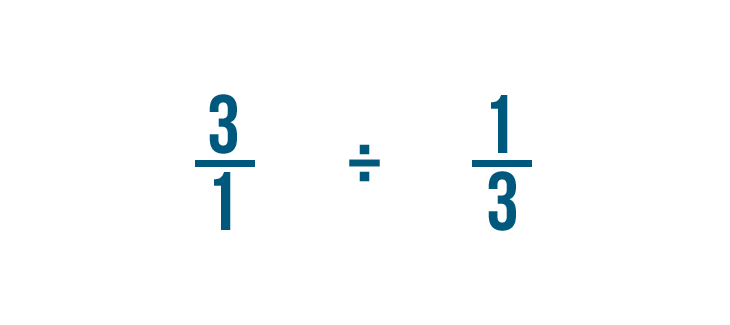
Antes de poder dividir, tenemos que hacer un cambio más.
-
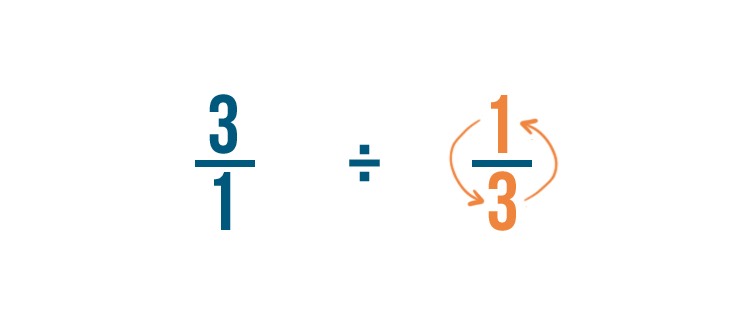
Cambiaremos el numerador y el denominador de la fracción por la que estamos dividiendo: 1/3 en este ejemplo.
-
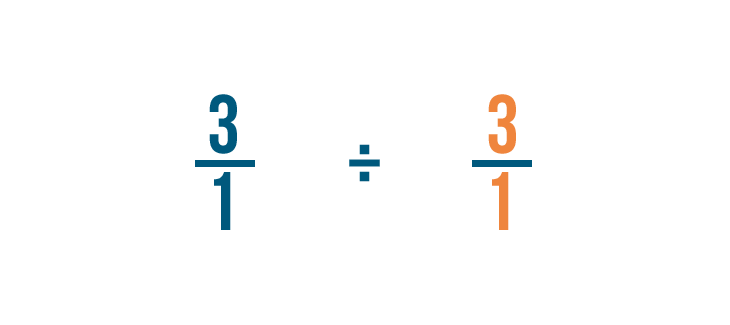
Así que 1/3 se convierte en 3/1.
-
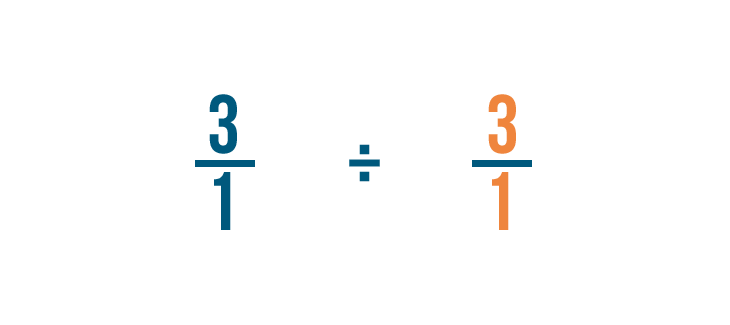
Esto se llama encontrar el recíproco, o inverso multiplicativo, de la fracción.
-
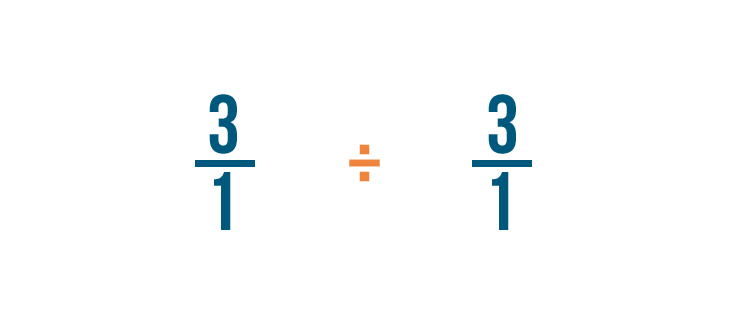
Como estamos cambiando nuestra fracción original, también cambiaremos el signo de división (÷) por un signo de multiplicación (x).
-
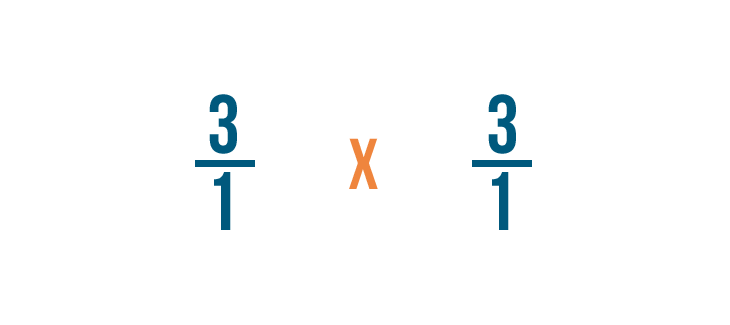
Esto es porque la multiplicación es la inversa de la división.
-
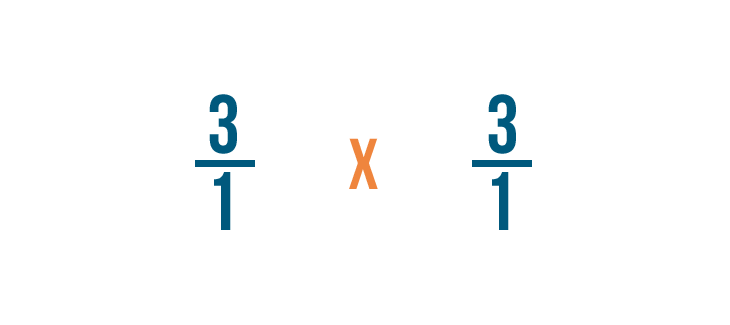
Ahora podemos tratar esto como un problema de multiplicación normal.
-
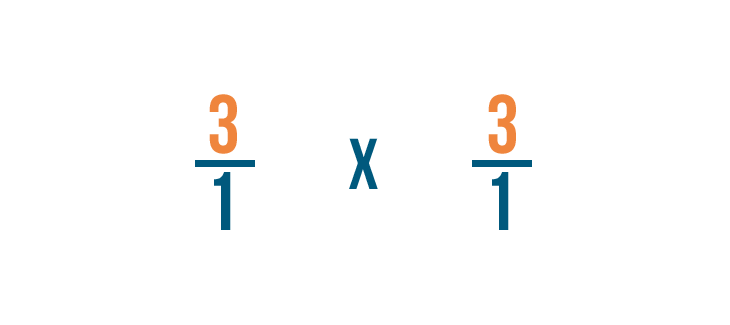
Primero, multiplicaremos los numeradores: 3 y 3.
-
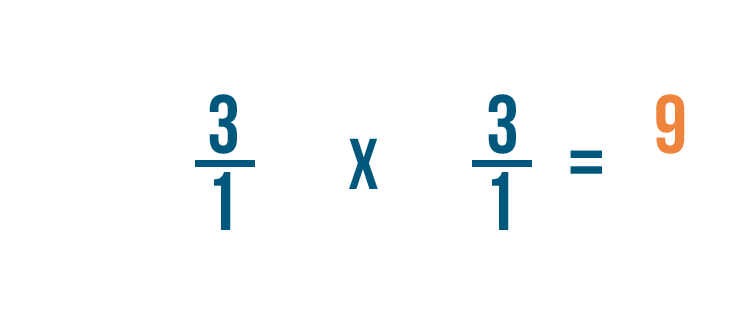
3 veces 3 es igual a 9, así que lo escribiremos junto a los numeradores.
-
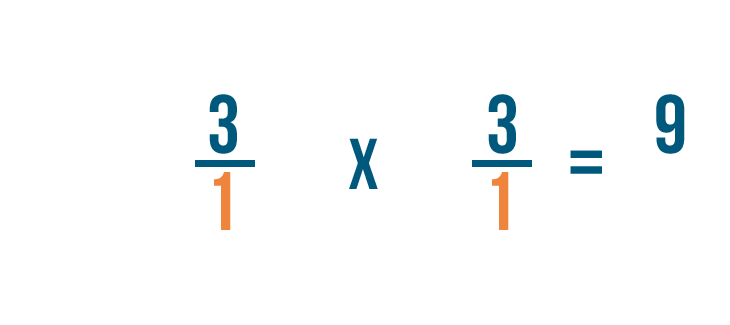
A continuación, multiplicaremos los denominadores: 1 y 1.
-
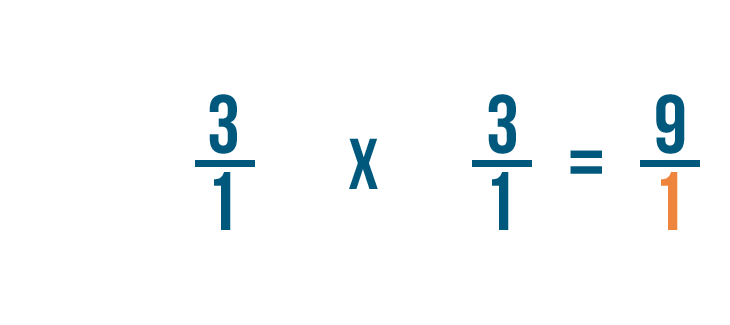
1 por 1 es igual a 1, así que escribiremos 1 junto al denominador.
-
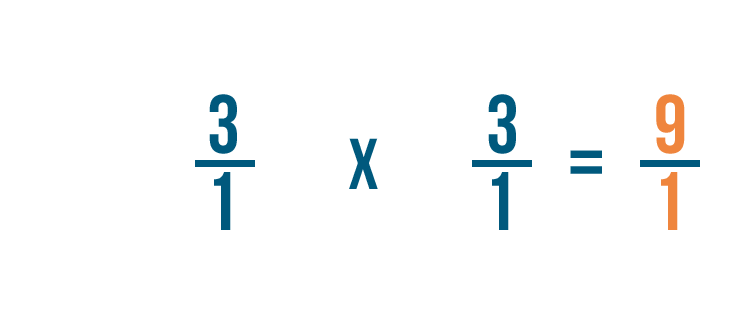
Como puedes ver, 3/1 x 1/3 = 9/1.
-
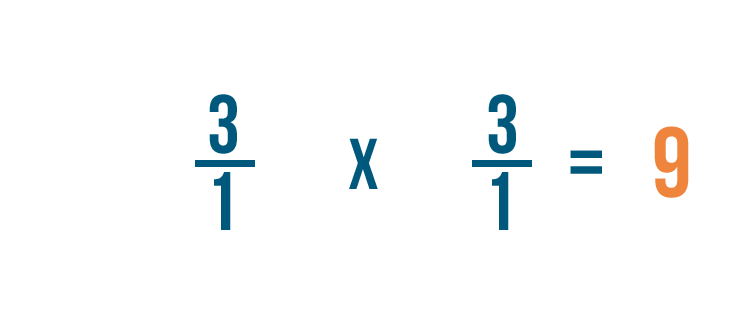
Recuerda que cualquier fracción mayor que 1 también se puede expresar como un número entero. Así que 9/1 = 9.
-
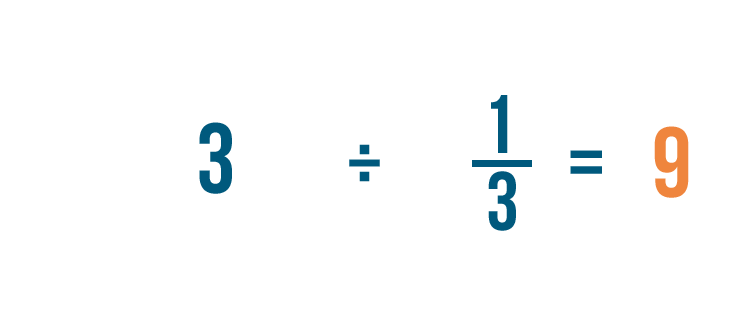
3 ÷ 1/3 = 9. Es decir, hay 9 tercios en 3.
-
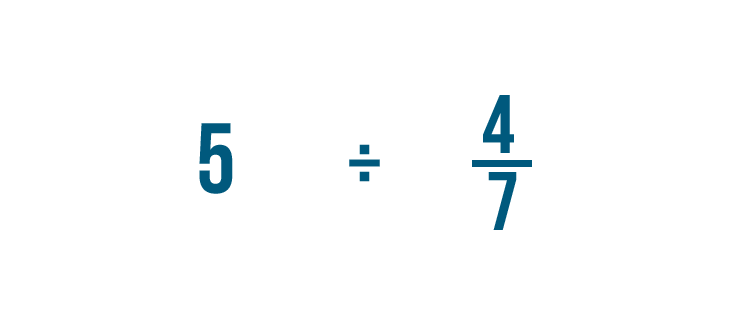
Intentemos otro ejemplo: 5 dividido por 4/7.
-
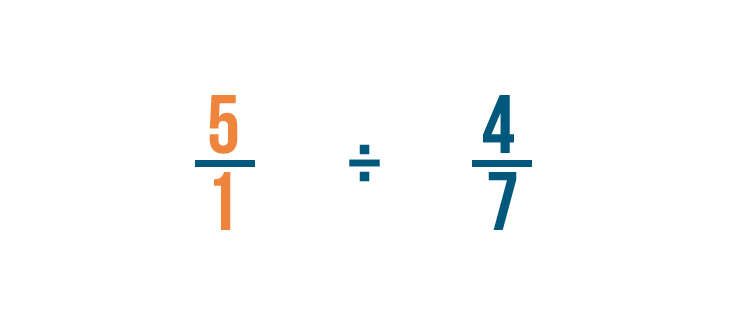
Como siempre, reescribiremos cualquier número entero, así que 5 se convierte en 5/1.
-
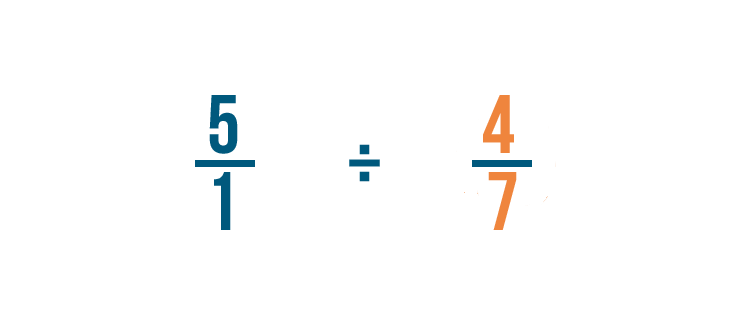
A continuación, encontraremos el recíproco de 4/7. Esa es la fracción entre la que vamos a dividir.
-
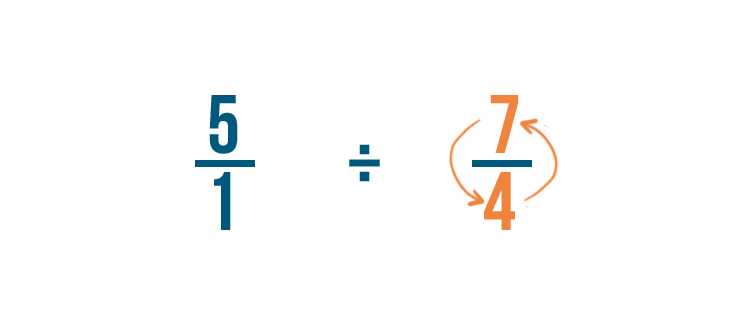
Para ello, cambiaremos el numerador y el denominador, de manera que 4/7 se convierte en 7/4.
-
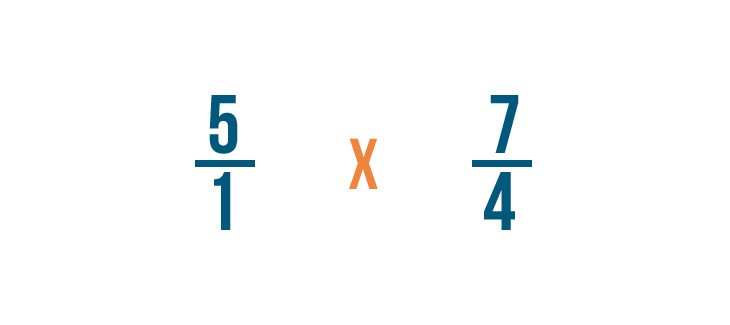
Entonces cambiaremos el signo de división (÷) por un signo de multiplicación (x).
-
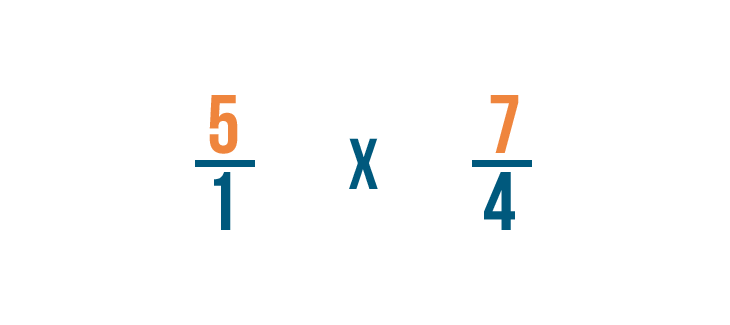
Ahora podemos multiplicar como lo haríamos normalmente. Primero, multiplicaremos los numeradores: 5 y 7.
-
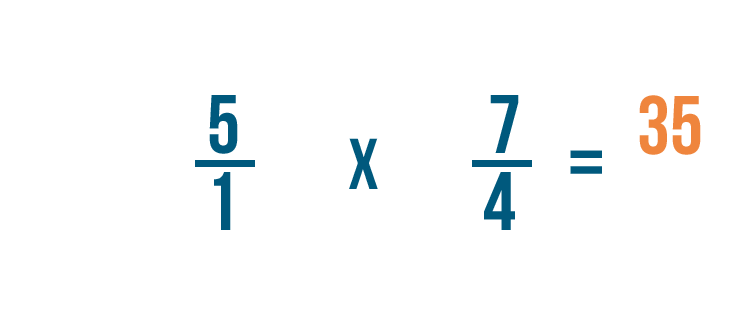
5 por 7 es igual a 35, así que lo escribiremos junto a los numeradores.
-
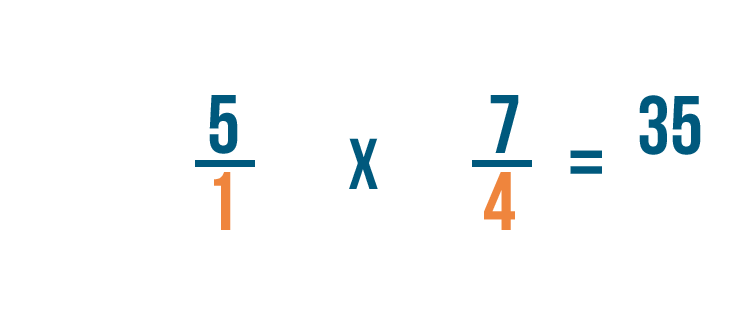
A continuación, multiplicaremos los denominadores: 1 y 4.
-
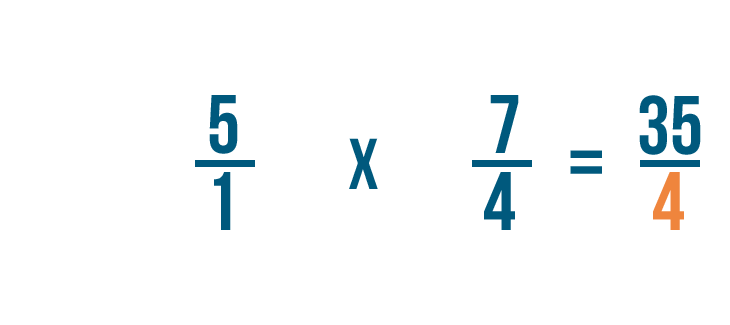
1 por 4 es igual a 4, así que lo escribiremos junto a los denominadores.
-
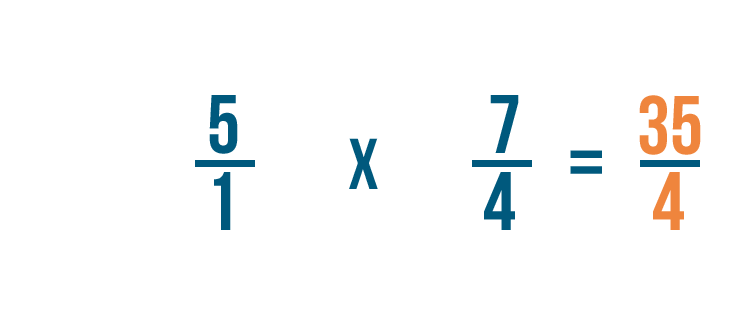
Así que 5/1 x 4/7 = 35/4.
-
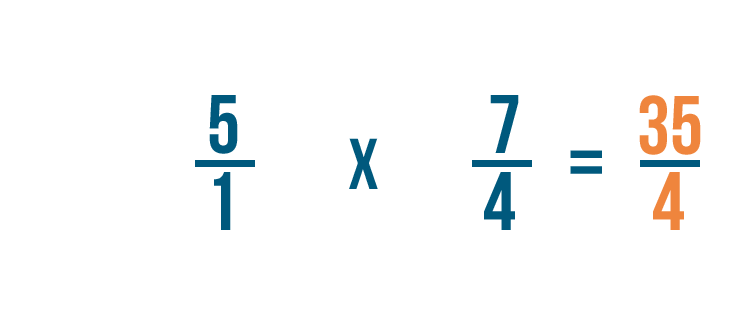
Como has aprendido antes, podemos convertir nuestra fracción impropia en un número mixto para que nuestra respuesta sea más fácil de leer.
-
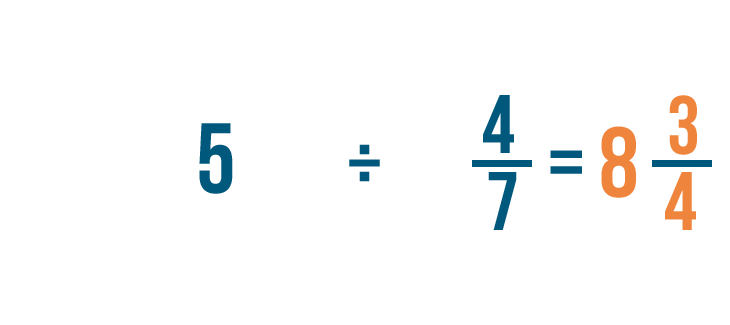
35/4 = 8 3/4. Así que 5 ÷ 4/7 = 8 3/4.

-
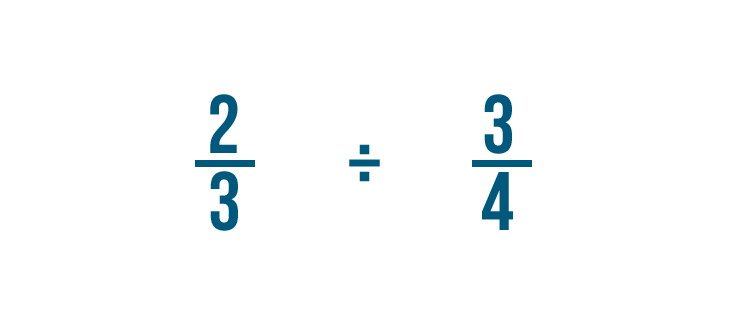
Intentemos un problema con dos fracciones: 2/3 ÷ 3/4. En este caso, queremos saber cuántos 3/4 hay en 2/3.
-
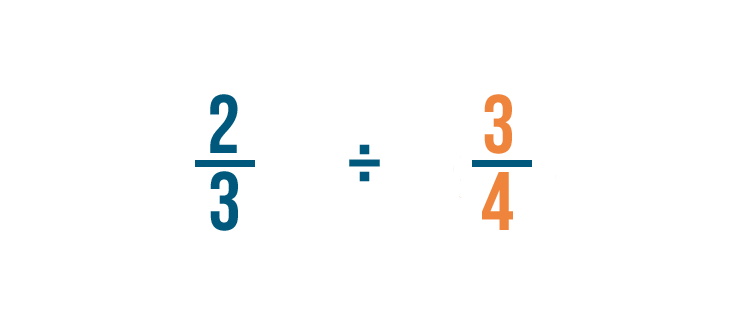
Primero, encontraremos el recíproco de la fracción entre la que estamos dividiendo: 3/4.
-
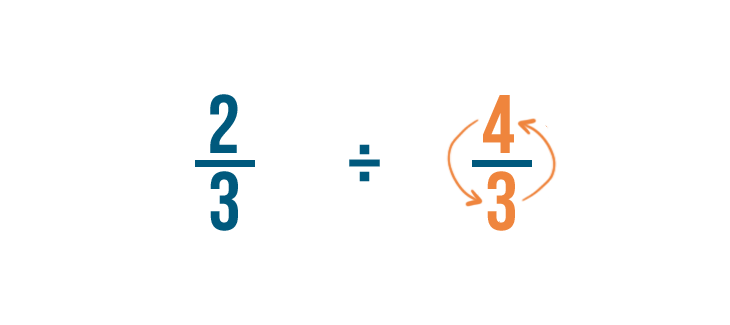
Para ello, cambiaremos el numerador y el denominador. Así, 3/4 se convierte en 4/3.
-
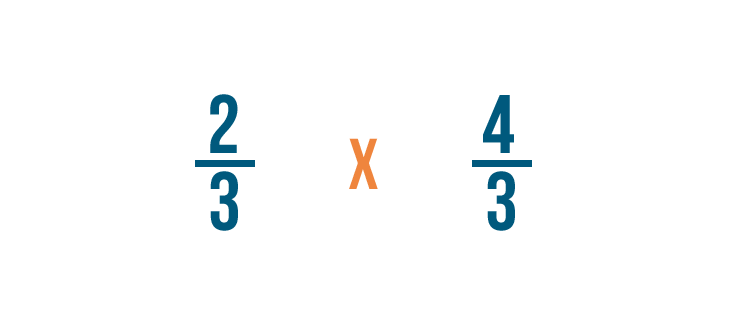
A continuación, cambiaremos el signo de división (÷) por un signo de multiplicación (x).
-
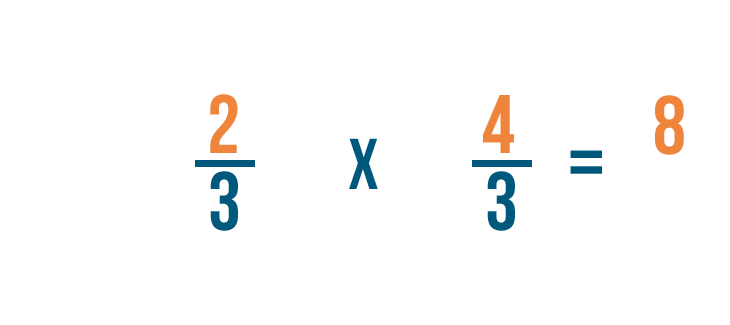
Ahora multiplicaremos los numeradores. 2 x 4 = 8, así que escribiremos 8 junto a los números superiores.
-
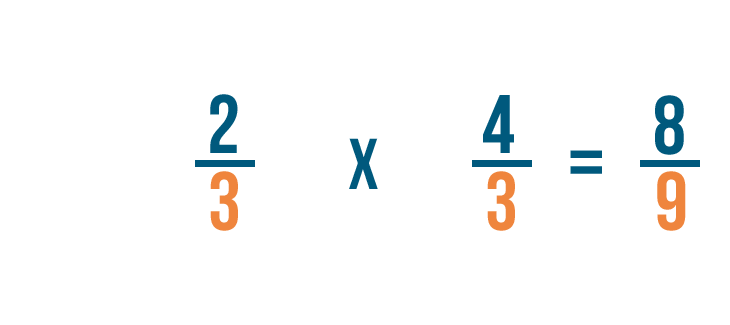
A continuación, multiplicaremos los denominadores. 3 x 3 = 9, así que escribiremos 9 junto a los números de abajo.
-
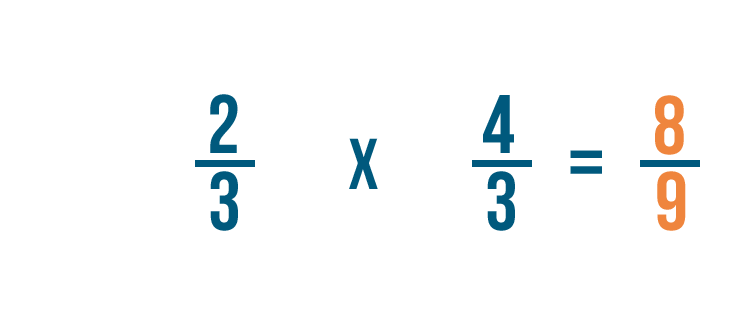
Así que 2/3 x 4/3 = 8/9.
-
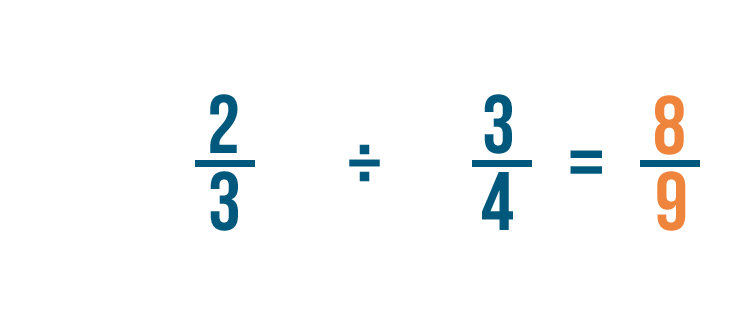
También podríamos escribirlo como 2/3 ÷ 3/4 = 8/9.
-
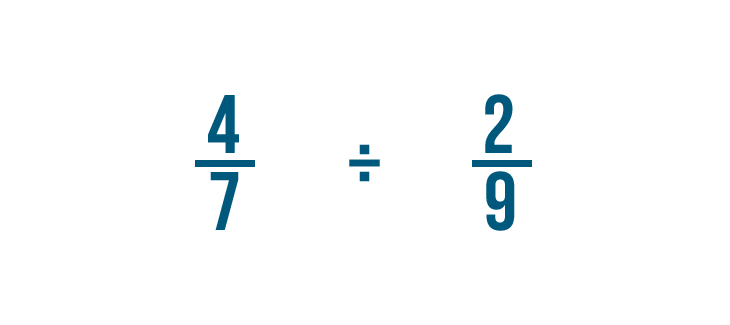
Intentemos otro ejemplo: 4/7 dividido por 2/9.
-
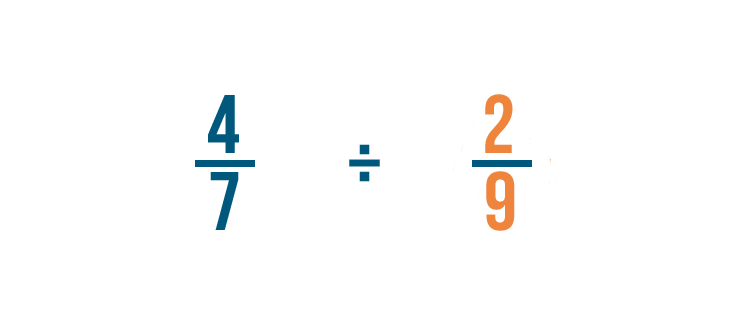
No hay números enteros, así que encontraremos el recíproco de la fracción por la que estamos dividiendo. Eso es 2/9.
-
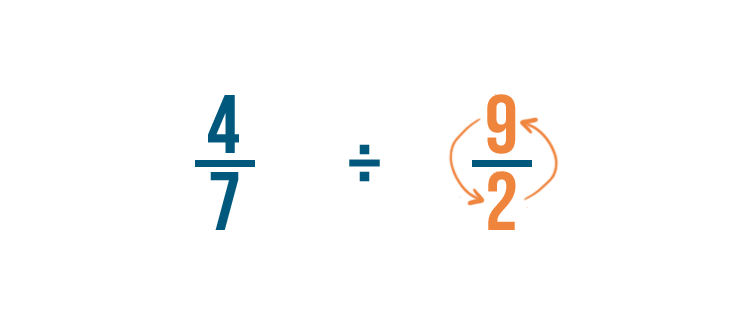
Para ello, cambiaremos el numerador y el denominador. Así, 2/9 se convierte en 9/2.
-
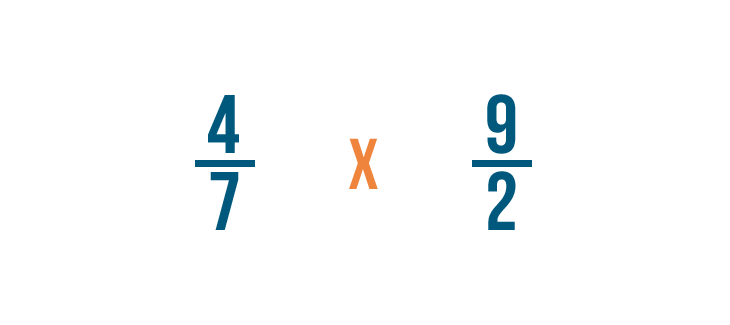
Ahora cambiaremos el signo de división (÷) por un signo de multiplicación (x) y multiplicaremos de forma normal.
-
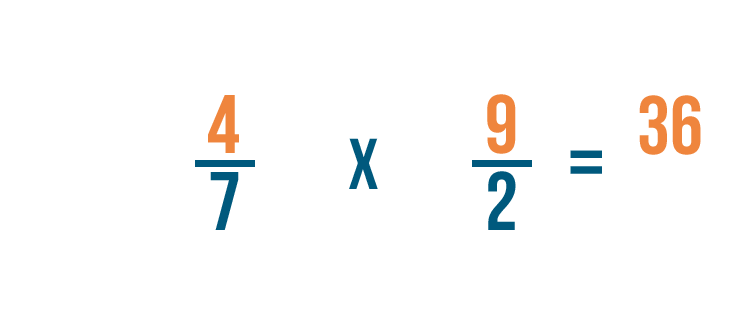
Primero, multiplicaremos los numeradores. 4 x 9 = 36.
-
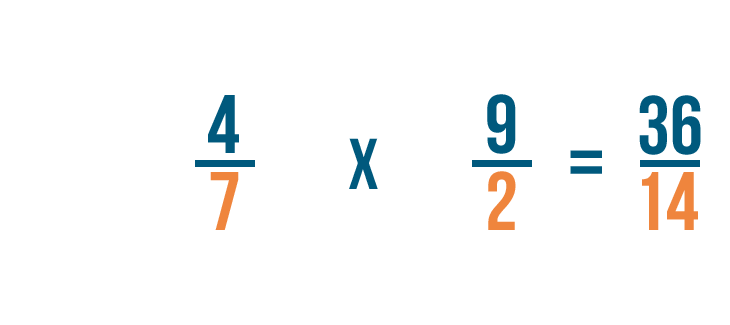
A continuación, multiplicaremos los denominadores. 7 x 2 = 14.
-
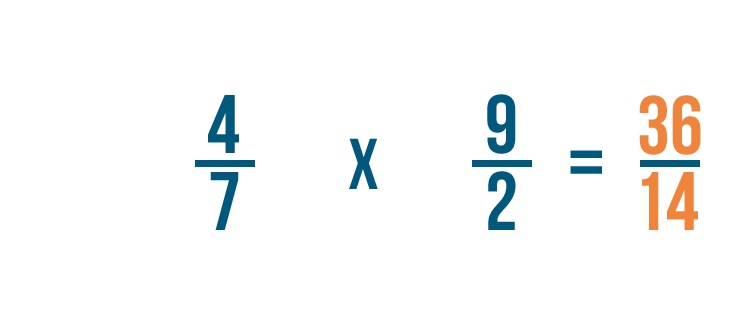
Así que 4/7 x 9/2 = 36/14. Al igual que antes, podrías convertir esta fracción impropia en un número mixto.
-
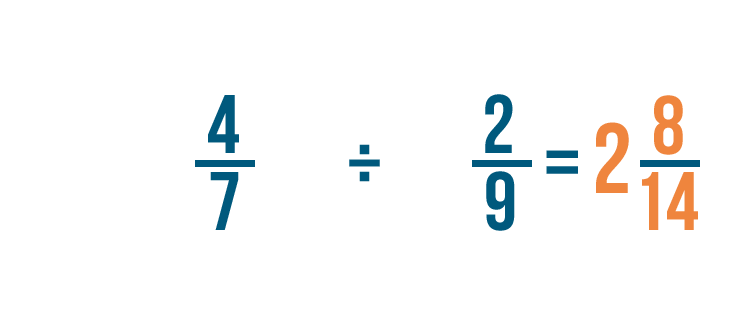
Así que 4/7 ÷ 2/9 = 2 8/14.

¡Intenta esto!
Intenta resolver los problemas de multiplicación de abajo.
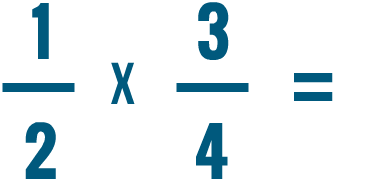
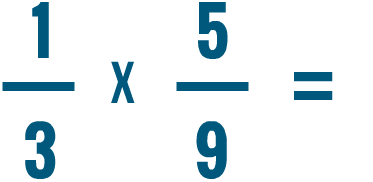
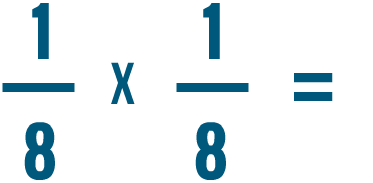
Multiplicar una fracción y un número entero
Multiplicar una fracción y un número entero es similar a multiplicar dos fracciones. Sólo hay un paso extra: Antes de poder multiplicar, tendrás que convertir el número entero en una fracción. Esta presentación te mostrará cómo hacerlo.
Haz clic en la presentación para aprender a multiplicar una fracción y un número entero.
¡Intenta esto!
Intenta resolver los problemas de multiplicación que aparecen a continuación.
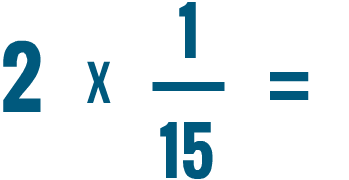
.
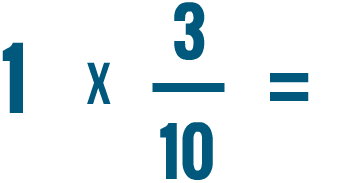
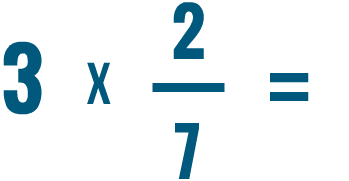
Dividiendo fracciones
En las últimas páginas, has aprendido a multiplicar fracciones. Es posible que hayas adivinado que también puedes dividir fracciones. Divides fracciones para ver cuántas partes de algo hay en otra cosa. Por ejemplo, si quieres saber cuántos cuartos de pulgada hay en cuatro pulgadas, puedes dividir 4 entre 1/4.
Intentemos otro ejemplo. Imagina que una receta pide 3 tazas de harina, pero en tu taza medidora sólo cabe 1/3, o un tercio, de taza. ¿Cuántos tercios de taza debes añadir?
Necesitaremos averiguar cuántos tercios de taza hay en tres tazas. Es decir, tendremos que dividir tres entre un tercio.
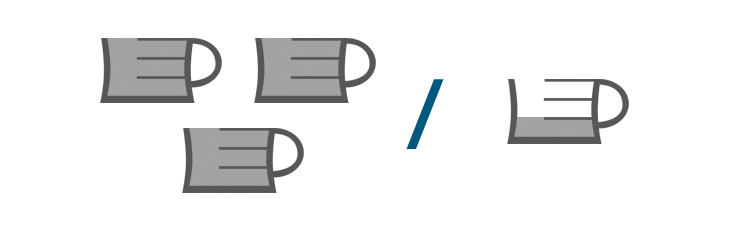
Escribiríamos el problema así:
3 ÷ 1/3
¡Inténtalo!
Intenta plantear estos problemas de división con fracciones. No te preocupes por resolverlos todavía!
Una receta pide 3/4 de taza de agua. Sólo tienes un vaso medidor de 1/8.

Resolución de problemas de división con fracciones
Ahora que sabemos cómo escribir problemas de división, vamos a practicar resolviendo algunos. Dividir fracciones es muy parecido a multiplicar. Sólo requiere un paso extra. Si puedes multiplicar fracciones, ¡también puedes dividirlas!
Haz clic en la presentación para aprender a dividir un número entero entre una fracción.
¡Intenta esto!
Intenta resolver estos problemas de división. No te preocupes por reducir la respuesta por ahora.
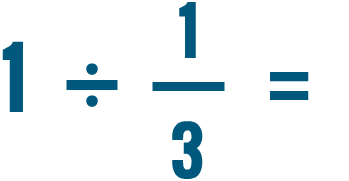
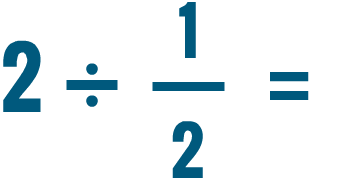
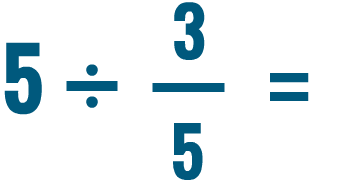
Dividir dos fracciones
Acabamos de aprender a dividir un número entero entre una fracción. Puedes utilizar el mismo método para dividir dos fracciones.
Haz clic en la presentación para aprender a dividir con dos fracciones.
¡Intenta esto!
Intenta resolver estos problemas de división. No te preocupes por reducir la respuesta por ahora.
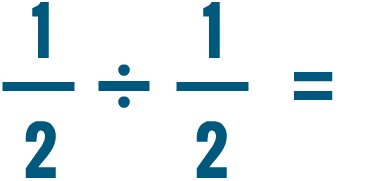
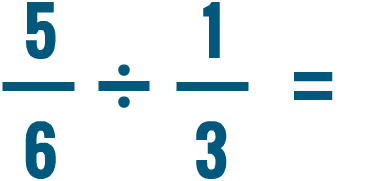
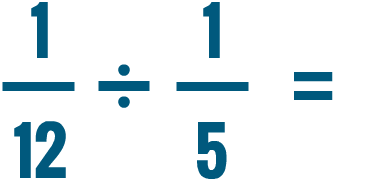
Multiplicar y dividir números mixtos
¿Cómo resolverías un problema como este?
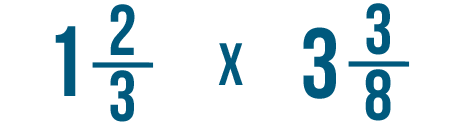
Como aprendiste en la lección anterior, siempre que vayas a resolver un problema con un número mixto tendrás que convertirlo primero en una fracción impropia. Luego puedes multiplicar o dividir como de costumbre.
Utilizando la cancelación para simplificar problemas
A veces podrías tener que resolver problemas como este:
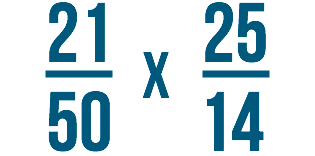
Ambas fracciones incluyen números grandes. Podrías multiplicar estas fracciones de la misma manera que cualquier otra fracción. Sin embargo, los números grandes como este pueden ser difíciles de entender. Puedes imaginarte 21/50, o veintiún cincuenta, en tu cabeza?
21/50 x 25/14 = 525/700
Incluso la respuesta parece complicada. Es 525/700, es decir, quinientos veinticinco septuagésimos. Si no te gusta trabajar con números grandes, puedes simplificar un problema como este utilizando un método llamado cancelación. Cuando cancelas las fracciones de un problema, estás reduciendo las dos al mismo tiempo.
La cancelación puede parecer complicada al principio, pero te mostraremos cómo hacerla paso a paso. Volvamos a ver el ejemplo que acabamos de ver.
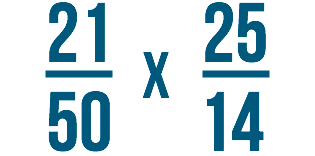
Paso 1
Primero, mira el numerador de la primera fracción y el denominador de la segunda. Queremos ver si se pueden dividir por el mismo número.
En nuestro ejemplo, parece que tanto 21 como 14 se pueden dividir por 7.
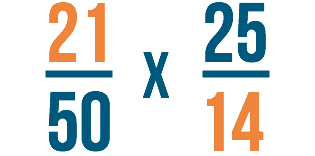
Paso 2
A continuación, dividiremos 21 y 14 por 7. Primero, dividiremos nuestro número superior de la izquierda: 21.
21 ÷ 7 = 3
Después dividiremos el número inferior de la derecha: 14.
14 ÷ 7 = 2
Escribiremos las respuestas de cada problema junto a los números que hemos dividido. Como 21 ÷ 7 es igual a 3, escribiremos 3 donde estaba el 21. 14 ÷ 7 es igual a 2, así que escribiremos 2 donde estaba el 14. Podemos tachar, o cancelar, los números con los que empezamos.
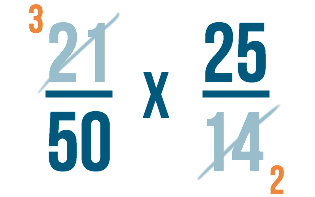
Nuestro problema parece ahora mucho más sencillo, ¿verdad?
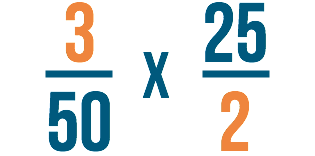
Paso 3
Veamos los otros números de la fracción. Esta vez miraremos el denominador de la primera fracción y el numerador de la segunda. ¿Pueden dividirse por el mismo número?
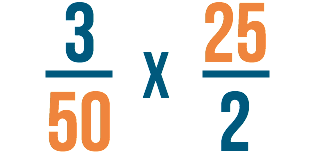
¡Observa que ambos pueden dividirse por 25! También te habrás dado cuenta de que ambos pueden dividirse por 5. Podríamos usar el 5 también, pero generalmente cuando estás cancelando, quieres buscar el mayor número por el que ambos números pueden dividirse. Así no tendrás que volver a reducir la fracción al final.
Paso 4
A continuación, cancelaremos igual que hicimos en el paso 2.
Dividiremos nuestro número inferior de la izquierda: 50.
50 ÷ 25 = 2
Entonces dividiremos el número superior de la derecha: 25.
25 ÷ 25 = 1
Escribiremos las respuestas a cada problema junto a los números que hemos dividido.
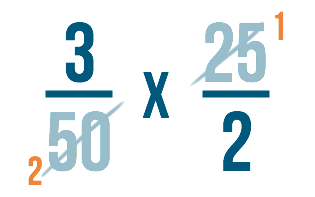
Paso 5
Ahora que hemos cancelado las fracciones originales, podemos multiplicar nuestras nuevas fracciones como haríamos normalmente. Como siempre, multiplica primero los numeradores:
3 x 1 = 3
Después multiplica los denominadores:
2 x 2 = 4
Así que 3/2 x 1/2 =3/4, o sea, tres cuartos.
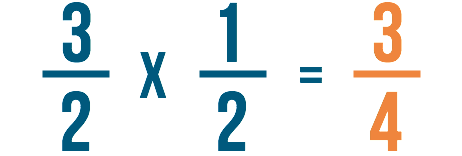
Paso 6
Por último, volvamos a comprobar nuestro trabajo. 525/700 habría sido nuestra respuesta si hubiéramos resuelto el problema sin cancelar. Si dividimos tanto 525 como 700 entre 175, podemos ver que 525/700 es igual a 3/4.
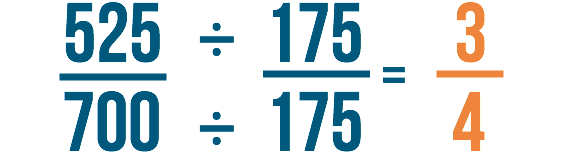
También podríamos decir que estamos reduciendo 525/700 a 3/4. Recuerda que cancelar es otra forma de reducir fracciones antes de resolver un problema. Obtendrás la misma respuesta, independientemente de cuándo las reduzcas.
Es/fracciones/convertir-porcentajes-decimales-y-fracciones/contenido
0 comentarios