¿Dónde está una función en un punto alto o bajo? El cálculo puede ayudar!
Un máximo es un punto alto y un mínimo es un punto bajo:
En una función que cambia suavemente un máximo o un mínimo es siempre donde la función se aplana (excepto en un punto de silla de montar).
¿Dónde se aplana? Donde la pendiente es cero.
¿Dónde es cero la pendiente? ¡La derivada nos lo dice!
Vamos a meternos de lleno con un ejemplo:
Ejemplo: Se lanza una pelota al aire. Su altura en cualquier momento t viene dada por:
h = 3 + 14t – 5t2
¿Cuál es su altura máxima?
Utilizando derivadas podemos encontrar la pendiente de esa función:
![]() h = 0 + 14 – 5(2t)
h = 0 + 14 – 5(2t)
= 14 – 10t
(Mira debajo de este ejemplo cómo hemos encontrado esa derivada.)
Ahora encuentra cuándo la pendiente es cero:
La pendiente es cero en t = 1,4 segundos
Y la altura en ese momento es:
Y así:
La altura máxima es de 12.8 m (a t = 1,4 s)
Un rápido repaso a las derivadas
Una derivada básicamente encuentra la pendiente de una función.
En el ejemplo anterior tomamos esto:
h = 3 + 14t – 5t2
y llegamos a esta derivada:
![]() h = 0 + 14 – 5(2t)
h = 0 + 14 – 5(2t)
= 14 – 10t
Lo que nos dice la pendiente de la función en cualquier momento t
Utilizamos estas Reglas de Derivación:
- La pendiente de un valor constante (como 3) es 0
- La pendiente de una recta como 2x es 2, por lo que 14t tiene una pendiente de 14
- Una función cuadrada como t2 tiene una pendiente de 2t, por lo que 5t2 tiene una pendiente de 5(2t)
- Y luego las sumamos: 0 + 14 – 5(2t)
¿Cómo sabemos que es un máximo (o un mínimo)?
¡Lo hemos visto en la gráfica! Pero por lo demás… las derivadas vuelven a acudir al rescate.
Toma la derivada de la pendiente (la segunda derivada de la función original):
La derivada de 14 – 10t es -10
Esto significa que la pendiente se hace continuamente más pequeña (-10): viajando de izquierda a derecha la pendiente empieza siendo positiva (la función sube), pasa por cero (el punto plano), y luego la pendiente se vuelve negativa (la función baja):

Una pendiente que se hace más pequeña (y pasa por 0) significa un máximo.
Esto se llama la prueba de la segunda derivada
En la gráfica anterior mostré la pendiente antes y después, pero en la práctica hacemos la prueba en el punto donde la pendiente es cero:
Prueba de la segunda derivada
Cuando la pendiente de una función es cero en x, y la segunda derivada en x es:
- menor que 0, es un máximo local
- mayor que 0, es un mínimo local
- igual a 0, entonces la prueba falla (aunque puede haber otras formas de averiguarlo)
«Segunda derivada: menor que 0 es un máximo, mayor que 0 es un mínimo»
Ejemplo: Encuentra los máximos y mínimos de:
y = 5×3 + 2×2 – 3x
La derivada (pendiente) es:
![]() y = 15×2 + 4x – 3
y = 15×2 + 4x – 3
Que es cuadrática con ceros en:
- x = -3/5
- x = +1/3
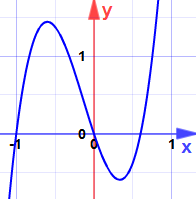
¿Podrían ser máximos o mínimos? (¡No mires todavía la gráfica!)
La segunda derivada es y» = 30x + 4
En x = -3/5:
En x = +1/3:
(Ahora puedes mirar la gráfica.)
Palabras
Un punto alto se llama máximo (plural máximos).
Un punto bajo se llama mínimo (plural mínimos).
La palabra general para máximo o mínimo es extremum (plural extrema).
Damos máximo (o mínimo) local cuando puede haber puntos más altos (o más bajos) en otro lugar pero no cerca.
Un ejemplo más
Ejemplo: Encuentra los máximos y mínimos de:
y = x3 – 6×2 + 12x – 5
La derivada es:
![]() y = 3×2 – 12x + 12
y = 3×2 – 12x + 12
Que es cuadrática con un solo cero en x = 2
¿Es un máximo o un mínimo?
La segunda derivada es y» = 6x – 12
En x = 2:
Y aquí está el porqué:
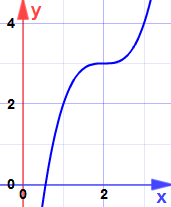
Es un punto de silla de montar… la pendiente sí se hace cero, pero no es ni máximo ni mínimo.
Debe ser diferenciable
Y hay un punto técnico importante:
La función debe ser diferenciable (la derivada debe existir en cada punto de su dominio).
Ejemplo: ¿Qué tal la función f(x) = |x| (valor absoluto)?
| |x| se ve así: |  |
¡En x=0 tiene un cambio muy puntiagudo!
De hecho no es diferenciable ahí (como se muestra en la página de diferenciables).
Así que no podemos usar este método para la función de valor absoluto.
La función también debe ser continua, pero cualquier función que sea diferenciable también es continua, así que no hay que preocuparse por eso.




0 comentarios