Demasiado grande para escribirlo pero no demasiado grande para Graham

Nuestro nuevo número favorito es mayor que la edad del Universo, tanto si se mide en años (aproximadamente 14.000 millones de años) como en segundos (4,343×1017 segundos). Es mayor que el número de Avogadro, un considerable 6,02214129 x 1023. Es el número de átomos de hidrógeno en 1 gramo de hidrógeno, que se denomina mol y es la unidad estándar para medir la cantidad de una sustancia en química o física.

El número de Graham es mayor que el número de átomos del Universo observable, que se cree que está entre 1078 y 1082. Es mayor que el primo 48 de Mersenne,

el mayor número primo que conocemos, que tiene la impresionante cifra de 17.425.170 dígitos. Y es mayor que el famoso googol, 10100 (un 1 seguido de 100 ceros), que fue definido en 1929 por el matemático estadounidense Edward Kasner y nombrado por su sobrino de nueve años, Milton Sirotta. (Puede que te suene, ya que Google recibió el nombre de este número, aunque se equivocó en la ortografía).

El número de Graham también es más grande que un googolplex, que Milton definió inicialmente como un 1, seguido de escribir ceros hasta cansarse, pero ahora se acepta comúnmente que es 10googol=10(10100). Un googleplex es bastante más grande que el 48º primo de Mersenne. Usted, o más bien un ordenador, puede escribir el 48º primo de Mersenne en su totalidad, los 17.425.170 dígitos. Pero, a pesar de que puedo decirle cuál es cualquier dígito del gúgolplex (el primero es un 1, el resto son todos 0), ninguna persona, ningún ordenador, ninguna civilización será capaz de escribirlo en su totalidad. Esto se debe a que no hay suficiente espacio en el Universo para escribir todos los dígitos del gúgol+1 de un gúgolplex. Como Kasner, y su colega James Newman, dijeron del googolplex (en su maravilloso libro de los años 40 Matemáticas y la imaginación, que introdujo al mundo estos números): «Te harás una idea del tamaño de este número tan grande pero finito por el hecho de que no habría espacio suficiente para escribirlo, si fueras a la estrella más lejana, recorriendo todas las nebulosas y poniendo ceros en cada centímetro del camino».

El número de Graham es más grande que el googolplex. Es tan grande que el Universo no contiene suficiente material sobre el que escribir sus dígitos: es literalmente demasiado grande para escribirlo. Pero este número es finito, también es un número entero, y a pesar de ser tan alucinantemente enorme sabemos que es divisible por 3 y termina en un 7.

Una gran fiesta

Los orígenes del número de Graham se remontan a 1928, cuando un joven y brillante matemático, Frank Ramsey, se dio cuenta de algo sorprendente cuando trabajaba en un artículo sobre lógica: el desorden completo parecía ser imposible. No importa lo complicado que parezca su sistema, siempre está garantizada la existencia de bolsas de orden de cualquier tamaño si el sistema es lo suficientemente grande.

Este resultado, que era sólo una pequeña parte del artículo en el que estaba trabajando, fue el comienzo de un nuevo campo de las matemáticas llamado Teoría de Ramsey. Esta área de las matemáticas se explica a menudo con el ejemplo de una fiesta. Supongamos que se celebra una fiesta y se quiere asegurar de que se invita a una buena mezcla de personas y se decide llevar la cuenta de quién conoce a quién. Supongamos que dibujas un mapa de las relaciones de todos tus amigos, uniendo dos personas con un borde azul si son amigos y con un borde rojo si son desconocidos. Entonces podrías terminar con algo así:

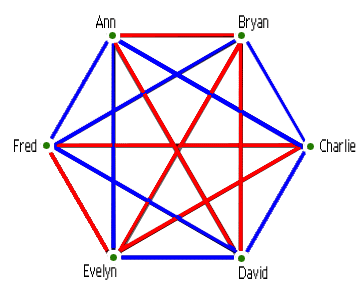
Ahora bien, esto parece bastante complicado y haría falta bastante información para describir quién está conectado por aristas rojas y quién por aristas azules. Pero si te acercas sólo a Ann, Bryan y David, todos están unidos por aristas rojas. Este triángulo rojo es un ejemplo de orden que se esconde en la desordenada red general. Cuanto más ordenado esté un sistema, más sencilla será su descripción. La red de amistad más ordenada es aquella que tiene todas las aristas del mismo color: es decir, todos son amigos o todos son desconocidos.

Ramsey descubrió que no importaba el orden que buscaras -ya fueran tres personas que fueran todas amigas y desconocidas o veinte personas que fueran todas amigas y desconocidas-, tenías garantizado encontrarlo siempre que el sistema en el que buscaras fuera lo suficientemente grande. Para garantizarte un grupo de tres personas que sean todas amigas o todas desconocidas necesitas una red de amistad de seis personas: cinco personas no son suficientes, como muestra este contraejemplo.

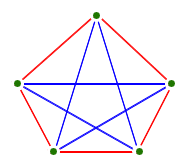
El número de personas que necesitas para garantizarte que encontrarás tres amigos o tres desconocidos se llama número de Ramsey R(3,3). Conocemos algunos números de Ramsey: hemos visto que R(3,3)=6, y se ha demostrado que R(4,4), el número de personas que necesitas para garantizar que encontrarás cuatro amigos o cuatro desconocidos, es 18. Pero nos topamos con un muro muy rápidamente. Por ejemplo, no sabemos cuál es R(5,5). Sabemos que está en algún lugar entre 43 y 49, pero eso es lo más cerca que podemos llegar por ahora.

Parte del problema es que los números en la teoría de Ramsey crecen increíblemente rápido. Si estamos viendo las relaciones entre tres personas, nuestra red tiene sólo tres aristas y hay unas razonables 23 formas posibles de colorear la red. Para cuatro personas hay seis aristas y 26=64 coloraciones posibles. Pero para las relaciones entre seis personas hay quince aristas y ya tenemos que considerar la difícil cifra de 215=32.768 coloraciones posibles. Los matemáticos están bastante seguros de que R(5,5) es igual a 43, pero no han encontrado la forma de demostrarlo. Una opción sería comprobar todas las posibles coloraciones de una red de 43 personas. Pero cada una de ellas tiene 903 aristas, así que habría que comprobar todas las 2903 coloraciones posibles, ¡más coloraciones que átomos hay en el Universo observable!

Demasiado grande para escribir, pero no demasiado grande para Graham

Los números grandes siempre han formado parte de la teoría de Ramsey, pero en 1971 el matemático Ronald Graham dio con un número que empequeñecía todos los anteriores. Estableció un límite superior para un problema en el área que fue, en ese momento, el mayor número definido explícitamente que se había publicado. En lugar de dibujar redes de relaciones entre personas en un papel plano, como hemos hecho hasta ahora, Graham se interesaba por las redes en las que las personas estaban sentadas en las esquinas de un cubo.

En esta imagen podemos ver que para un corte diagonal plano particular a través del cubo, uno que contiene cuatro de las esquinas, todas las aristas son rojas. Pero no todas las coloraciones de los cubos tridimensionales tienen esa rebanada de un solo color. Por suerte, los matemáticos también tienen una forma de pensar en cubos de mayor dimensión. Cuanto mayor es la dimensión, más esquinas hay: un cubo tridimensional tiene 8 esquinas, un cubo de cuatro dimensiones tiene 16 esquinas, un cubo de cinco dimensiones tiene 32 esquinas y así sucesivamente. Graham quería saber qué dimensión tiene que tener el cubo para garantizar que exista una rodaja de un solo color.

Ronald Graham que nos dio su hermoso número. Imagen: Cheryl Graham.

Graham consiguió encontrar un número que garantizaba que esa rebanada existía para un cubo de esa dimensión. Pero este número, como hemos mencionado antes, era absolutamente masivo, tan grande que es demasiado grande para escribirlo dentro del Universo observable. Sin embargo, Graham fue capaz de definir explícitamente este número utilizando una ingeniosa notación llamada notación de flecha hacia arriba que extiende nuestras operaciones aritméticas comunes de suma, multiplicación y exponenciación.

Podemos pensar en la multiplicación como una suma repetida:

Si definimos que la operación de la flecha única, , es la exponenciación, entonces:

entonces podemos definir la operación de doble flecha como

Podemos seguir construyendo nuevas operaciones repitiendo las anteriores. La siguiente sería la triple flecha

¡una torre de potencias de 3 que tiene 7.625.597.484.987 niveles de altura! (Vea aquí para leer sobre la notación de flecha hacia arriba con más detalle.)

El número que ha llegado a conocerse como el número de Graham (no es el número exacto que aparecía en su artículo inicial, es un número un poco más grande y más fácil de definir que explicó a Martin Gardner poco después) se define utilizando esta notación de flecha hacia arriba, en un proceso acumulativo que crea torres de potencias de tres que rápidamente se convierten en espirales más allá de cualquier magnitud que podamos imaginar.

Pero lo que nos encanta del número de Graham es que esta cantidad inimaginablemente grande no es un concepto teórico: es un número exacto. Sabemos que es un número entero, de hecho es fácil ver que este número es un múltiplo de tres por la forma en que se define como una torre de potencias de tres. Y los matemáticos han aprendido mucho sobre los procesos utilizados para definir el número de Graham, incluido el hecho de que una vez que una torre de potencias es lo suficientemente alta, los dígitos decimales de la derecha acabarán siendo los mismos, sin importar cuántos niveles más se añadan a la torre de potencias. El número de Graham puede ser demasiado grande para escribirlo, pero sabemos que termina en siete. Las matemáticas tienen el poder no sólo de definir lo inimaginable, sino también de investigarlo.

Acerca de este artículo

Rachel Thomas y Marianne Freiberger son las editoras de Plus. Este artículo es un extracto editado de su nuevo libro Numericon: Un viaje por la vida oculta de los números.