=================================================================================
En la teoría clásica de la difracción, la difracción de Bragg se produce cuando las ondas de partículas cargadas o de radiación electromagnética con una longitud de onda comparable al espacio atómico inciden en una muestra cristalina. Las ondas reflejadas en centros de dispersión adyacentes deben tener una diferencia de camino igual a un número integral de longitudes de onda. Las ondas dispersas interfieren constructivamente si permanecen en fase. Por lo tanto, la diferencia de camino entre las ondas de electrones reflejadas desde los planos superior e inferior en la figura 3882 es igual a la longitud total (AO+BO). Suponiendo que los planos hkl están separados por una distancia dhkl y que la onda incide y se refleja en ángulos θB, tanto AB como BC son iguales a dsin(θB) y la diferencia de trayectoria total debe ser igual a 2dsin(θB).
Como se discute en la página2678, podemos tener,
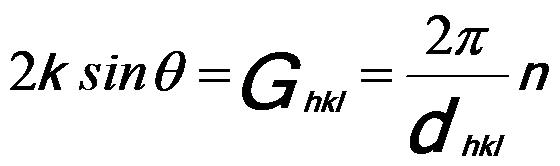 ——————————————
——————————————
donde,
n — El múltiplo entero del Ghkl más pequeño que se permite,
k = 2π/λ.
Por tanto, podemos obtener la conocida condición de difracción de Bragg, dada por,
nλ = 2dhklsin(θB) ——————————————–
donde,
n — Un número entero, el orden de reflexión;
dhkl — El espaciado de la red de (hkl);
λ — La longitud de onda de la partícula cargada o de las ondas de radiación electromagnética;
θB — El ángulo de Bragg que es el ángulo entre el vector de onda incidente y los planos de la red como se muestra en la figura 3882,
hkl — Los índices de Miller.
El ángulo de Bragg θB es un concepto muy importante en la teoría de la difracción, por ejemplo, ampliamente utilizado para explicar los fenómenos de difracción de electrones y rayos X. Se obtienen intensidades muy fuertes conocidas como picos de Bragg en el patrón de difracción cuando las ondas dispersas satisfacen la condición de Bragg. El ángulo entre las ondas incidentes y reflejadas es igual a 2θB como se muestra en la Figura 3882.
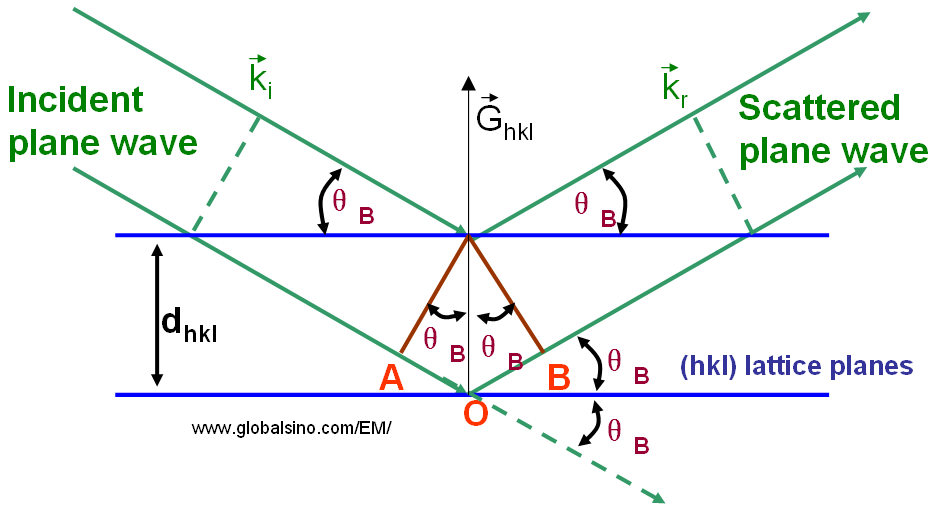
La diferencia de camino entre las ondas reflejadas es igual a AO + BO.
Para las estructuras FCC y BCC, las constantes de red vienen dadas por, (Puede descargar el archivo excel para sus propios cálculos)
—————–
La tabla 3882a muestra que los electrones interactúan con 1 electrón, muchos electrones, 1 núcleo y muchos núcleos en los sólidos.
| Interacción con electrón(es) | Interacción con el núcleo/núcleo |
1 electrón
|
Muchos electrones | 1 núcleo | Muchos núcleos |
|---|---|---|---|---|---|
| Tipo de dispersión | Inelástica | Inelástica | Casielástica | Elástica | Inelástica |
| Efecto Compton del electrón; Excitación de electrones (desde 50 eV hasta unos pocos keV: EDS y EELS) | Excitación de plasmones (< 50 eV, muestra TEM de ~100 nm); efecto Cerenkov | Dispersión Rutherford; dispersión de fonones (< 1 eV, calor) | Dispersión de Bragg | Bremsstrahlung | |
La tabla 3882b enumera algunos ejemplos de ángulos de Bragg a varios voltajes del haz para un espaciado d típico. Los ángulos de Bragg se obtuvieron con la ecuación 3882b (para n = 1).
Tabla 3882b. Ángulos de Bragg a varios voltajes del haz para un espaciado d típico.
| Tensión de aceleración (kV) | Longitud de onda (nm) | Cristales | d-espaciamiento (nm) | Ángulo de Bragg (° & mrad) | 100 | 0.0037 | Cristales biológicos típicos | 10 | 0,0106° (0,19 mrad) | 200 | 0,0025 | Níquel (Ni) | 0,203 | 0.353° (6,16 mrad) |
En los experimentos reales, a diferencia de la dispersión difusa, los picos de Bragg provienen de la estructura ordenada de largo alcance. Las muestras cristalinas tienen que ser inclinadas en un goniómetro en TEM para:
i) Observar las franjas de red y las estructuras cristalinas.
ii) Determinar la orientación del cristal.
iii) Observar el contraste de difracción de los defectos de red con ciertas reflexiones de Bragg o con orientación conocida.
iv) Determinar el vector de Burgers de los defectos de red.
Tabla 3882c. Guiones de micrografía digital para calcular los ángulos de reflexión de los cristales.
| Estructura de los cristales | Scripts |
| Difracción de electrones, XRD | |
| BCC | Difracción de electrones, XRD |
0 comentarios