A veces, hay más de una forma de resolver un problema. Tenemos que aprender a comparar el rendimiento de diferentes algoritmos y elegir el mejor para resolver un problema en particular. Al analizar un algoritmo, se considera principalmente la complejidad temporal y la complejidad espacial. La complejidad temporal de un algoritmo cuantifica la cantidad de tiempo que tarda un algoritmo en ejecutarse en función de la longitud de la entrada. Del mismo modo, la complejidad espacial de un algoritmo cuantifica la cantidad de espacio o memoria que necesita un algoritmo para ejecutarse en función de la longitud de la entrada.
La complejidad temporal y espacial depende de muchas cosas como el hardware, el sistema operativo, los procesadores, etc. Sin embargo, no consideramos ninguno de estos factores al analizar el algoritmo. Sólo consideraremos el tiempo de ejecución de un algoritmo.
Empecemos con un ejemplo sencillo. Supongamos que nos dan una matriz $A$ y un número entero $x$ y tenemos que encontrar si $x$ existe en la matriz $A$.
La solución sencilla a este problema es recorrer toda la matriz $A$ y comprobar si algún elemento es igual a $x$.
for i : 1 to length of A if A is equal to x return TRUEreturn FALSECada una de las operaciones en el ordenador tarda aproximadamente un tiempo constante. Dejemos que cada operación tome $c$ tiempo. El número de líneas de código ejecutadas depende en realidad del valor de $x$. Durante el análisis del algoritmo, en la mayoría de los casos consideraremos el peor escenario, es decir, cuando $x$ no está presente en la matriz $A$. En el peor de los casos, la condición if se ejecutará $N$ veces, siendo $N$ la longitud de la matriz $A$. Por lo tanto, en el peor de los casos, el tiempo total de ejecución será $(N * c + c)$. $N * c$ para la condición if y $c$ para la sentencia return ( ignorando algunas operaciones como la asignación de $i$ ).
Como podemos ver el tiempo total depende de la longitud del array $A$. Si la longitud del array aumenta el tiempo de ejecución también aumentará.
El orden de crecimiento es cómo el tiempo de ejecución depende de la longitud de la entrada. En el ejemplo anterior, podemos ver claramente que el tiempo de ejecución depende linealmente de la longitud del array. El orden de crecimiento nos ayudará a calcular el tiempo de ejecución con facilidad. Ignoraremos los términos de orden inferior, ya que éstos son relativamente insignificantes para una entrada grande. Utilizamos una notación diferente para describir el comportamiento límite de una función.
$O$-notación:
Para denotar el límite superior asintótico, utilizamos $O$-notación. Para una función dada $g(n)$, denotamos por $O(g(n))$ (pronunciado «big-oh de g de n») el conjunto de funciones:
$O(g(n)) =$ { $f(n)$ : existen constantes positivas $c$ y $n_0$ tales que $0 \le f (n) \le c * g(n)$ para todo $n \ge n_0$ }
$Omega$-notación:
Para denotar la cota inferior asintótica, utilizamos $Omega$-notación. Para una función dada $g(n)$, denotamos por $\Omega(g(n))$ (pronunciado «big-omega de g de n») el conjunto de funciones:
$\Omega(g(n)) =$ {$f(n)$ : existen constantes positivas $c$ y $n_0$ tales que $0 \le c * g(n) \le f(n)$ para todo $n \ge n_0$ }
$Theta$-notation:
Para denotar una cota ajustada asintótica, utilizamos $$Theta$-notation. Para una función dada $g(n)$, denotamos por $Theta(g(n))$ (pronunciado «big-theta de g de n») el conjunto de funciones:
$Theta(g(n)) =$ { $f (n)$ : existen las constantes positivas $c_1,\Nyc_2$ y $n_0$ tales que $0 \le c_1 * g(n) \le f (n) \le c_2 * g(n)$ para todo $n \gt n_0$ }
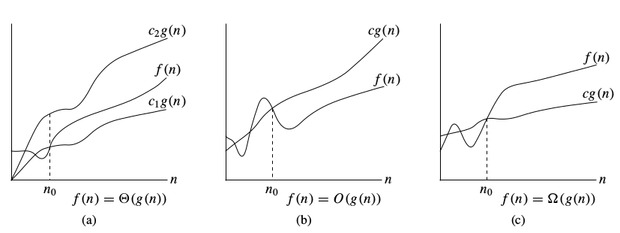
Notaciones de complejidad temporal
Al analizar un algoritmo, consideramos principalmente la anotación $O$ porque nos dará un límite superior del tiempo de ejecución, es decirEs decir, el tiempo de ejecución en el peor de los casos.
Para calcular la anotación $O$ ignoraremos los términos de orden inferior, ya que éstos son relativamente insignificantes para entradas grandes.
Dejemos $f(N) = 2 * N^2 + 3 * N + 5$
$O(f(N)) = O(2 * N^2 + 3 * N + 5) = O(N^2)$
Consideremos algún ejemplo:
int count = 0;for (int i = 0; i < N; i++) for (int j = 0; j < i; j++) count++;Veamos cuántas veces se ejecutará count++.
Cuando $i = 0$, se ejecutará $0$ veces.
Cuando $i = 1$, se ejecutará $1$ veces.
Cuando $i = 2$, se ejecutará $2$ veces y así sucesivamente.
El número total de veces que se ejecutará count++ es $0 + 1 + 2 + … + (N-1) = \frac{N * (N-1)}{2}$. Así que la complejidad temporal será $O(N^2)$.
int count = 0;for (int i = N; i > 0; i /= 2) for (int j = 0; j < i; j++) count++;Este es un caso complicado. A primera vista, parece que la complejidad es $O(N * logN)$. $N$ para el bucle de $j$ y $logN$ para el bucle de $i$.Pero es un error. Veamos por qué.
Piensa cuántas veces se ejecutará count++.
Cuando $i = N$, se ejecutará $N$ veces.
Cuando $i = N / 2$, se ejecutará $N / 2$ veces.
Cuando $i = N / 4$, se ejecutará $N / 4$ veces y así sucesivamente.
El número total de veces que se ejecutará count++ es $N + N / 2 + N / 4 + … + 1 = 2 * N$. Así que la complejidad de tiempo será $O(N)$.
La tabla que se muestra a continuación es para ayudarle a entender el crecimiento de varias complejidades de tiempo comunes, y así ayudarle a juzgar si su algoritmo es lo suficientemente rápido para obtener un Aceptado ( suponiendo que el algoritmo sea correcto).
| Longitud de la Entrada (N) | Peor Aceptado ¡Algoritmo |
|---|---|
| $\le $ | $O(N!), O(N^6)$ | $le $ | $O(2^N * N^2)$ |
| $le $ | $O(2^N * N)$ |
| $le 100$ | $O(N^4)$ | $le 400$ | $O(N^3)$ |
| $le 2K$ | $O(N^2 * logN)$ | $le 10K$ | $O(N^2)$ |
| $le 1M$ | $O(N * logN)$ |
| $le 100M$ | $O(N) O(logN), O(1)$ |
Ir al siguiente tutorial
0 comentarios