Calculadora de pendientes

Si se conocen los 2 puntos

Si se conoce 1 punto y la pendiente

Inclinación, a veces llamada gradiente en matemáticas, es un número que mide la inclinación y la dirección de una línea, o una sección de una línea que conecta dos puntos, y se denota generalmente por m. En general, la inclinación de una línea se mide por el valor absoluto de su pendiente, m. Cuanto mayor sea el valor, más inclinada será la línea. Dado m, es posible determinar la dirección de la línea que describe m basándose en su signo y valor:

• Una recta es creciente, y va hacia arriba de izquierda a derecha cuando m > 0
• Una recta es decreciente, y va hacia abajo de izquierda a derecha cuando m < 0
• Una recta tiene una pendiente constante, y es horizontal cuando m = 0
• Una recta vertical tiene una pendiente indefinida, ya que daría lugar a una fracción con 0 como denominador. Consulta la ecuación que se proporciona a continuación.

La pendiente es esencialmente el cambio en la altura sobre el cambio en la distancia horizontal, y a menudo se denomina «subida sobre bajada». Tiene aplicaciones en gradientes en geografía así como en ingeniería civil, como la construcción de carreteras. En el caso de una carretera, la «subida» es el cambio de altitud, mientras que el «recorrido» es la diferencia de distancia entre dos puntos fijos, siempre que la distancia para la medición no sea lo suficientemente grande como para que la curvatura de la tierra deba considerarse como un factor. La pendiente se representa matemáticamente como:

x2 – x1

m =

y2 – y1

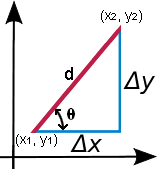
En la ecuación anterior, y2 – y1 = Δy, o cambio vertical, mientras que x2 – x1 = Δx, o cambio horizontal, como se muestra en el gráfico proporcionado. También se puede ver que Δx y Δy son segmentos de línea que forman un triángulo rectángulo con hipotenusa d, siendo d la distancia entre los puntos (x1, y1) y (x2, y2). Como Δx y Δy forman un triángulo rectángulo, es posible calcular d mediante el teorema de Pitágoras. Consulta la calculadora de triángulos para obtener más detalles sobre el teorema de Pitágoras, así como la forma de calcular el ángulo de inclinación θ proporcionada en la calculadora anterior. Brevemente:

d = √(x2 – x1)2 + (y2 – y1)2

La ecuación anterior es el teorema de Pitágoras en su raíz, donde ya se ha resuelto la hipotenusa d, y los otros dos lados del triángulo se determinan restando los dos valores de x e y dados por dos puntos. Dados dos puntos, es posible hallar θ mediante la siguiente ecuación:

m = tan(θ)

Dados los puntos (3,4) y (6,8) halla la pendiente de la recta, la distancia entre los dos puntos y el ángulo de inclinación:

m =

8 – 4

6 – 3

=

d = √(6 – 3)2 + (8 – 4)2 = 5

= tan(θ)

θ = tan-1(

) = 53.13°

Aunque esto está fuera del alcance de esta calculadora, aparte de su uso lineal básico, el concepto de pendiente es importante en el cálculo diferencial. Para las funciones no lineales, la tasa de cambio de una curva varía, y la derivada de una función en un punto determinado es la tasa de cambio de la función, representada por la pendiente de la recta tangente a la curva en ese punto.