En estadística, el rango es la dispersión de sus datos desde el valor más bajo hasta el más alto de la distribución. Es una medida de variabilidad comúnmente utilizada.
Junto con las medidas de tendencia central, las medidas de variabilidad le proporcionan estadísticas descriptivas para resumir su conjunto de datos.
El rango se calcula restando el valor más bajo del valor más alto. Mientras que un rango grande significa alta variabilidad, un rango pequeño significa baja variabilidad en una distribución.
Tabla de contenidos
Calcular el rango
La fórmula para calcular el rango es:
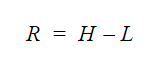
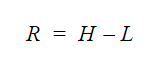
- . R = rango
- H = valor más alto
- L = valor más bajo
El rango es la medida de variabilidad más fácil de calcular. Para encontrar el rango, siga estos pasos:
- Ordenar todos los valores de su conjunto de datos de menor a mayor.
- Restar el valor más bajo del valor más alto.
Este proceso es el mismo independientemente de si sus valores son positivos o negativos, o números enteros o fracciones.
| Participante | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Edad | 37 | 19 | 31 | 29 | 21 | 26 | 33 | 36 |
Primero, ordenamos los valores de menor a mayor para identificar el valor más bajo (L) y el más alto (H).
| Edad | 19 | 21 | 26 | 29 | 31 | 33 | 36 | 37 |
|---|
Luego resta el valor más bajo al más alto.
R = H – L
R = 37 – 19 = 18
El rango de nuestro conjunto de datos es de 18 años.
¿Cuál es la utilidad del rango?
El rango generalmente te da un buen indicador de la variabilidad cuando tienes una distribución sin valores extremos. Cuando se empareja con las medidas de tendencia central, el rango puede informarle sobre el alcance de la distribución.
Pero el rango puede ser engañoso cuando tiene valores extremos en su conjunto de datos. Un valor extremo en los datos le dará un rango completamente diferente.
| Edad | 19 | 21 | 29 | 31 | 33 | 36 | 61 |
|---|
Utilizando el mismo cálculo, obtenemos un resultado muy diferente esta vez:
R = H – L
R = 61 – 19 = 42
Con un valor atípico, nuestro rango es ahora de 42 años.
En el ejemplo anterior, el rango indica mucha más variabilidad en los datos de la que realmente hay. Aunque tenemos un gran rango, la mayoría de los valores se agrupan en torno a un medio claro.
Debido a que sólo se utilizan dos números, el rango se ve fácilmente influenciado por los valores atípicos. No puede informarle sobre la forma de la distribución de los valores por sí mismo.
Para obtener una idea clara de la variabilidad de sus datos, el rango se utiliza mejor en combinación con otras medidas de variabilidad como el rango intercuartil y la desviación estándar.
Preguntas frecuentes sobre el rango
En estadística, el rango es la dispersión de tus datos desde el valor más bajo hasta el más alto de la distribución. Es la medida más sencilla de la variabilidad.
No. Debido a que la fórmula del rango resta el número más bajo del número más alto, el rango es siempre cero o un número positivo.
La variabilidad se mide más comúnmente con los siguientes estadísticos descriptivos:
- Rango: la diferencia entre los valores más altos y más bajos
- Rango intercuartil: el rango de la mitad media de una distribución
- Desviación estándar: distancia media de la media
- Varianza: media de las distancias al cuadrado de la media
Mientras que la tendencia central le indica dónde se encuentra la mayoría de sus puntos de datos, la variabilidad resume lo alejados que están sus puntos entre sí.
Los conjuntos de datos pueden tener la misma tendencia central pero diferentes niveles de variabilidad o viceversa. Juntos, le dan una imagen completa de sus datos.

0 comentarios