Cómo comprobar la escuadra, esquinas de 90 grados

Usando la regla 3 4 5 para construir en forma de L & ¡Paredes cuadradas, habitaciones, techos y mucho más!

Los consejos de esta página cubren:

• Por qué necesitas comprobar la cuadratura cuando construyes cosas (principalmente para ahorrarte montones de disgustos más adelante..)
• Cómo escuadrar un marco/techo/habitación/edificio de cuatro lados
• Cuadrar dos lados con la regla 3 4 5 (pythagoras theorum)
• Tipos de escuadras de carpintero (herramientas) disponibles

¿Por qué es tan importante construir cosas perfectamente cuadradas?

Construir cosas como paredes, suelos o cubiertas perfectamente verticales, a plomo y a escuadra es, siempre que sea posible, esencial. Te ayudará a evitar problemas y a ahorrar mucho tiempo más adelante y es también la manera más sólida de formar estructuras de forma práctica.

A veces, como en las casas antiguas, por ejemplo, hay que hacer excepciones. A veces hay que «dividir la diferencia», o aceptar el menor de los males y hacer lo que se pueda. En estos casos siempre me imagino lo que haría si fuera mi propia casa o, lo que es lo menos perceptible/más agradable a la vista.

<p>Construir las paredes a escuadra asegurará que los materiales de lámina como el pladur sean rápidos y fáciles de instalar. Las placas de las paredes deben estar a escuadra y niveladas para que las vigas del tejado funcionen. Las cubiertas de jardín y las vigas del suelo construidas a escuadra serán mucho más fáciles de colocar. La lista es interminable, pero unos 10 minutos más para comprobar que todo está a escuadra en las primeras etapas podrían ahorrarle horas o incluso días más tarde.

No construir las cosas a nivel y de forma correcta sólo le provocará dolores de cabeza y trabajo extra más adelante. Las puertas se abrirán o cerrarán solas si no instala los revestimientos de las puertas a nivel y a escuadra. Los ingletes serán difíciles de conseguir, y habrá que hacer más trazados, lo que significa trabajo extra, dolores de cabeza – y tiempo/coste.

Aunque hay muchas escuadras de carpintería disponibles para comprobar los 90°, cuando se construye un gran muro de madera o una terraza de jardín, por ejemplo, suelen ser demasiado pequeñas para asegurar que la estructura tiene esquinas perfectas de 90°.

Hay dos métodos sencillos y fáciles de recordar que yo utilizo.

Cómo comprobar la escuadra en un marco de cuatro lados

Para formar un marco cuadrado o rectangular ambas placas (superior e inferior) deben tener la misma longitud, y todos los montantes o viguetas deben tener la misma longitud entre sí también. Una vez clavado, para comprobar que la estructura es cuadrada simplemente mida de esquina a esquina.

Si las medidas no son iguales, tire de la esquina larga hacia el centro de la estructura hasta que se igualen. Una vez idénticas, la estructura está perfectamente escuadrada. Clave un listón temporalmente a través de tres o cuatro viguetas o montantes para mantenerlo a escuadra hasta que se fije en su sitio.

Esta es también una buena manera de comprobar que las placas de las paredes están a escuadra antes de fijarlas en su sitio antes de empezar a cortar las vigas del tejado.

¿Menos de cuatro lados a escuadra? Utiliza el teorema de Pitágoras

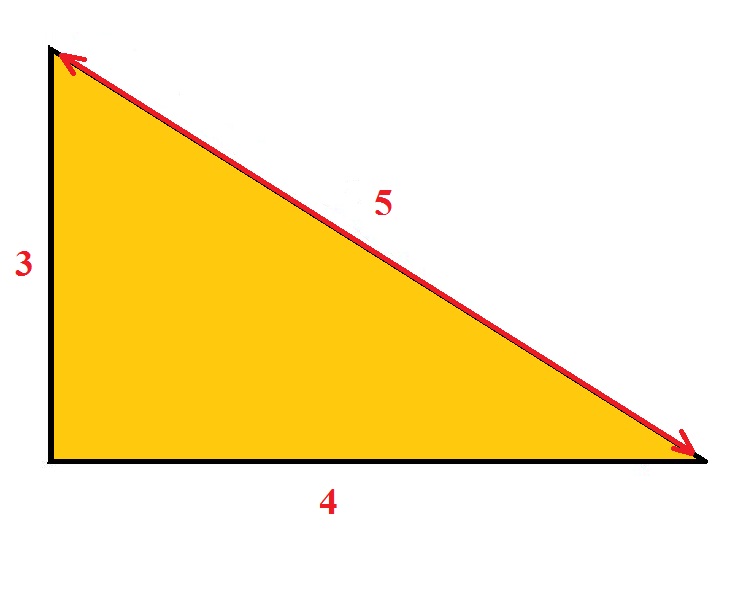
A veces no tienes cuatro esquinas para medir y, por tanto, se requiere un método diferente para comprobar si las esquinas de los ángulos rectos son cuadradas. Esto podría ser, por ejemplo, cuando se construyen paredes interiores y se colocan placas de pared en forma de L. La imagen que aparece a continuación le indica todo lo que necesita saber para comprobar que un marco, una pared u otra estructura es cuadrada utilizando la regla 3 4 5. Cuando mides por un lado 3 y por el otro 4 la medida entre los dos puntos debe medir siempre 5 si la esquina es de 90 grados.

No importa la unidad de medida que utilices, siempre que la mantengas igual para los tres lados. Puede ser 3/4/5mm, 3/4/5 pies, 3/4/5 metros o 3/4/5 millas!

Cuando uso este método para colocar dos placas base, fijo una placa en su lugar y muevo la otra alrededor hasta que obtengo un ‘5’ perfecto y entonces lo fijo también.

La razón por la que esto funciona es por la antigua fórmula de comprobación del cuadrado – Pythagorus theorum. Es decir 3 al cuadrado, más 4 al cuadrado = 5 al cuadrado. 3 x 3 = 9, 4 x 4 = 16. Súmalos y obtienes 25 que también es 5 x 5.

También hay muchos tipos de escuadras de carpintero disponibles para comprobar la escuadra a una escala más pequeña y para marcar las líneas de escuadra cuando se establece.