Cálculo – Determinación de valores mínimos y máximos Parte I

Cálculo – Determinación de
Mínimos &Valores Máximos
Parte I

Uno de los usos más importantes del cálculo es la determinación de los valores mínimos y máximos. Esto tiene sus aplicaciones en la fabricación, las finanzas, la ingeniería y una gran cantidad de otras industrias. Antes de examinar un ejemplo del mundo real, debemos aprender a calcular dichos valores.

Utilicemos para nuestro primer ejemplo, la ecuación 2X2 -5X -7 = 0

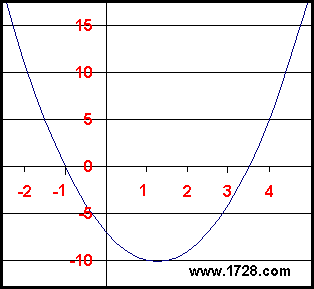
Esta es una ecuación cuadrática en una variable. Es decir, es una ecuación de la forma:ax2 + bx + c = 0
Con ecuaciones de este tipo, sabemos que cuando el término «a» es positivo, la gráfica de la curva será «cóncava hacia arriba» (en forma de U) y, por tanto, la ecuación tendrá un valor mínimo pero no un valor máximo (vale – técnicamente, el valor máximo es el infinito). Observando el gráfico vemos que el punto mínimo es aproximadamente X = 1,5 e Y = -10. ¿Hay alguna forma de determinar el punto mínimo sin tener que graficar la ecuación y obtener un valor exacto? Sí, la hay. Mira la gráfica. Si los valores de la pendiente se calcularan para los puntos de la izquierda de la curva, podrías ver que la pendiente siempre sería negativa, pero se vuelve «menos negativa» cuanto más se acerca la curva al mínimo (la parte inferior). Si se calculara la pendiente a lo largo del lado derecho de la curva, el valor sería siempre positivo y los valores de la pendiente se harían más grandes cuanto más lejos del «fondo» estuvieran los puntos.

Entonces, es lógico pensar que la pendiente es cero en ese punto «inferior» y, por tanto, la derivada es cero también en ese punto.
Entonces, tomemos la derivada de 2X2 -5X -7 = 0 que es:

4X – 5Cuando 4X -5 es igual a cero, X =1,25 lo que significa que en ese punto existe un valor mínimo. En cuanto al valor de ‘Y’, vamos a la ecuación original e introducimos el valor de X como 1,25. Y = 2X2 -5X -7Y = 2*(1,25)2 -5*1,25 -7Y = -10.125Entonces, en el punto X=1,25, Y= -10,125 existe un valor mínimo.

En este ejemplo sabíamos que estábamos obteniendo un valor mínimo porque lo graficamos. Además, dijimos que la «regla» de las ecuaciones cuadráticas es tal que cuando el término ‘a’ es positivo, la curva será «cóncava hacia arriba». Todavía hay un tercer método para determinar si un punto es un valor máximo o mínimo.
Si tomamos la segunda derivada y si ese valor es positivo, entonces estamos ante un valor mínimo.
En este ejemplo, tomando la derivada de la derivada tenemos el valor 4 que es positivo y por lo tanto sabemos que se trata de un mínimo.

Para ecuaciones del tipo aX2 + bX + c =0, una herramienta muy útil es la Calculadora de Ecuaciones Cuadráticas. Ésta no sólo calcula las raíces de la ecuación, sino que también mostrará la derivada y el punto en el que existe el máximo o el mínimo.

El segundo ejemplo que veremos es muy similar al anterior, salvo que es «cóncavo hacia abajo» en lugar de «cóncavo hacia arriba». Si crees que has entendido los conceptos presentados hasta ahora, entonces pasa a la segunda parte

Bien, examinemos esta ecuación:

-4X2 + 4X + 13 = 0Como se trata de una ecuación cuadrática en una variable con el término ‘a’ negativo, sabemos que la gráfica de la curva tendrá forma «cóncava hacia abajo» (con forma de ∩) y tendrá un valor máximo pero no un valor mínimo (vale, si quieres ser técnico, su valor mínimo es el infinito negativo. ¿Estás contento ahora?).
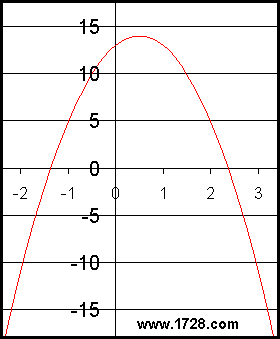
Aprendimos en el primer ejemplo que la forma de calcular un punto máximo (o mínimo) es encontrar el punto en el que la derivada de una ecuación es igual a cero.La derivada de esta ecuación es: