¿Qué son los estiramientos y encogimientos horizontales?
Los estiramientos y encogimientos horizontales, respectivamente, tiran horizontalmente de la gráfica base, o la juntan, mientras dejan la intersección y sin cambios para anclar la gráfica.
Definición
Para la función base f (x) y una constante k, donde k > 0 y k ≠ 1, la función dada por
g(x) = f (kx),
se puede esbozar encogiendo horizontalmente f (x) en un factor de 1/k si k > 1
o
estirando horizontalmente f (x) por un factor de 1/k
si 0 < k < 1.
Un estiramiento o encogimiento horizontal por un factor de 1/k significa que el punto (x, y) de la gráfica de f(x) se transforma en el punto (x/k, y) de la gráfica de g(x).
Ejemplos de estiramientos y encogimientos horizontales
Considera las siguientes funciones de base,
(1) f (x) = x2 – 3,
(2) g(x) = cos (x).
La representación gráfica de la función (1), f (x), es una parábola. Cómo supones que es la gráfica de
y1(x) = f (4x)
? Utilizando la definición de f (x), podemos escribir y1(x) como,
y1(x) = f (4x) = (4x)2 – 3 = 16×2-3.
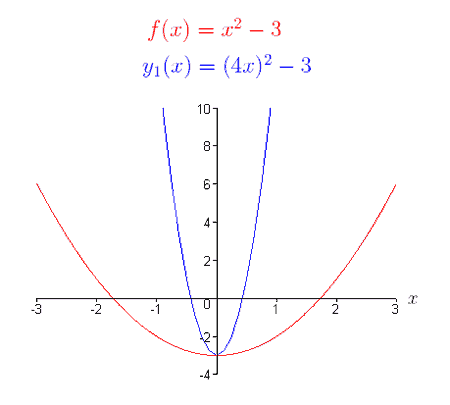
Basándonos en la definición de encogimiento horizontal, la gráfica de y1(x) debería parecerse a la gráfica de
f (x), encogida horizontalmente por un factor de 1/4. Observa las gráficas de f (x) e y1(x).
La función (2), g (x), es una función coseno. Qué aspecto tendría la gráfica de
y2(x) = g(2/3x)
? Utilizando nuestros conocimientos sobre tramos horizontales, la gráfica de y2(x) debería parecerse a la gráfica de la base g(x) estirada horizontalmente por un factor de 3/2. Para comprobarlo, podemos escribir y2(x) como,
y2(x) = g(2/3x) = cos (2/3x),
Construye una tabla de valores, y traza la gráfica de la nueva función. Como puedes ver, la gráfica de y2(x) es en realidad la gráfica de la base g(x) estirada horizontalmente por un factor de 3/2.

0 comentarios