Lorsque j’avais dix ans, ma famille a fait un voyage à New York où j’ai pu voir l’un des pièges à touristes les plus célèbres de la ville : l’Empire State Building. La vue au sommet du gratte-ciel était incroyable, couvrant la ville sur des kilomètres. Je me souviens avoir pensé que la chute du haut de l’immeuble jusqu’au trottoir en dessous devait être terriblement longue. Depuis ce voyage, j’ai pris connaissance de la légende qui circule selon laquelle un penny tombé du sommet de l’Empire State Building tuerait une personne s’il la touchait. Il m’a toujours semblé étrange qu’un objet aussi minuscule puisse porter un coup mortel simplement parce qu’il est lâché d’une hauteur stupéfiante. Cependant, j’ai décidé de mettre mon intuition à l’épreuve et d’utiliser la science pour déterminer si mon scepticisme était justifié ou non. Alors, un penny lâché du haut de l’Empire State Building va-t-il tuer une personne s’il la touche ?
Maintenant que j’avais ma question, j’ai décidé de former une hypothèse : Si un penny est lâché du haut de l’Empire State Building, il atteindra une vitesse suffisamment élevée pour tuer une personne lors de l’impact. Il s’agit de l’hypothèse alternative, tandis que l’hypothèse nulle propose que rien ne se passe, et qu’un penny lâché à la hauteur de l’Empire State Building n’atteindra pas une vitesse suffisamment élevée pour tuer quelqu’un.
Dans ce cas, la variable causale (indépendante x) est la hauteur à laquelle le penny est lâché. L’Empire State Building compte 103 étages, soit 1 250 pieds, ou 381 mètres dans le reste du monde, jusqu’au dernier étage où le penny serait lancé. La variable de réponse (y dépendante) est la vitesse atteinte par le penny, car la vitesse dépend de la variable x de la hauteur. Cela fait de la variable y un point final souple, et elle est plus facile à mesurer. En fin de compte, nous sommes plus préoccupés par le point final dur, qui serait la mort si le penny atteint une vitesse suffisamment élevée pour tuer quelqu’un. Cependant, une expérience conçue pour tester la mort d’une personne en tant que variable de réponse serait plutôt contraire à l’éthique, car elle ferait courir un risque immense aux sujets testés. Par conséquent, les scientifiques ne peuvent vraiment effectuer que des tests plus théoriques qui examinent la physique derrière un penny en chute libre.
La variable de réponse dans ce scénario est la base de la façon dont ce mythe a même commencé. En théorie, un penny voyageant en chute libre depuis ce genre de hauteur atteindrait une vitesse mortelle. On suppose que cela est dû à la force de gravité. Une équation cinématique, ou une équation mesurant le mouvement d’un objet, peut décrire cette situation particulière :
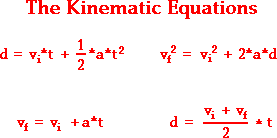
L’équation qui s’applique à cette théorie de la chute libre est celle en bas à gauche, qui se traduit par vitesse finale = vitesse initiale + accélération * temps. Pour résoudre cette équation, le même site qui m’a donné la formule note que la vitesse initiale sera de 0 mètre par seconde, 0 m/s, car il ne se déplace pas au départ. L’accélération d’un objet en chute libre est toujours, en théorie, de -9,8 m/s. Cela tient compte de l’impact de la gravité sur l’objet. D’après cet article, il faudrait environ 9 secondes à un penny lâché depuis l’Empire State Building pour toucher le sol. Ainsi, d’après mes calculs effectués à l’aide de la formule, un penny atteindrait une vitesse d’environ 88 m/s, soit environ 196 mph. Bien que ce soit une vitesse assez rapide, ce n’est toujours pas suffisant pour tuer quelqu’un.
Mon calcul n’est également précis que si nous vivions dans le vide et que toute résistance de l’air était supprimée. Ce n’est évidemment pas le cas, et nous devons prendre en compte l’impact de la traînée et de la résistance de l’air. À un certain moment, un objet atteint sa vitesse terminale, qui se produit lorsque la résistance de l’air est équivalente à la force de gravité. À cette vitesse terminale, un centime atteindrait sa vitesse maximale, et la vitesse ne pourrait pas aller plus loin. Selon ce document compilé par des membres du département de physique et d’astronomie de l’université de Leicester, leurs calculs indiquent qu’un penny atteindrait sa vitesse terminale à 40,1 m/s, soit 89,7 mph. C’est nettement moins que le calcul original qui ne prenait en compte que la gravité, et cette vitesse n’est certainement pas suffisante pour tuer quelqu’un.
 Une expérience réalisée par Louis Bloomfield, professeur de physique à l’Université de Virginie, arrive à une conclusion similaire que les calculs théoriques montrent. Dans son expérience, Bloomfield a utilisé un grand ballon météorologique rempli d’hélium pour lancer des centimes à partir d’un distributeur à différentes hauteurs. Dans cette étude, Bloomfield manipule la variable x, la hauteur, pour déterminer la vitesse terminale de la chute d’un centime, qui est la variable y. Cette étude lui a permis de constater que, bien que le ballon ait été placé à différentes hauteurs, les centimes ont atteint leur vitesse maximale à environ 15 mètres, puis n’ont plus jamais accéléré. À cette hauteur, le penny atteint sa vitesse terminale et flotte simplement vers le sol à partir de là.
Une expérience réalisée par Louis Bloomfield, professeur de physique à l’Université de Virginie, arrive à une conclusion similaire que les calculs théoriques montrent. Dans son expérience, Bloomfield a utilisé un grand ballon météorologique rempli d’hélium pour lancer des centimes à partir d’un distributeur à différentes hauteurs. Dans cette étude, Bloomfield manipule la variable x, la hauteur, pour déterminer la vitesse terminale de la chute d’un centime, qui est la variable y. Cette étude lui a permis de constater que, bien que le ballon ait été placé à différentes hauteurs, les centimes ont atteint leur vitesse maximale à environ 15 mètres, puis n’ont plus jamais accéléré. À cette hauteur, le penny atteint sa vitesse terminale et flotte simplement vers le sol à partir de là.
Une célèbre émission de la chaîne Discovery Channel, Mythbusters, a également mené une expérience sur ce sujet. Les stars de l’émission, Jamie et Adam, ont créé un pistolet qui lancerait un penny à une vitesse d’environ 64,4 m/s, ce qui correspond à ce que certaines autres études ont suggéré comme vitesse terminale d’un penny en chute libre ; c’est un peu élevé par rapport à certains calculs. Jamie et Adam ont ensuite testé leur pistolet à sous en le tirant sur un crâne en gel pour voir s’il y aurait un impact. Même à 64,4 m/s (144 mph), le penny a traversé la couche de gel, mais n’a même pas fait de bosse dans le crâne de fortune. Cette preuve est convaincante lorsqu’on envisage la possibilité d’une mort par penny, et à la lumière de ce test, cela semble peu probable.
Sur la base de mes recherches sur ce mythe, les superstitieux peuvent dormir tranquilles. Bien qu’un penny tombant d’un gratte-ciel comme l’Empire State Building atteigne une vitesse qui peut être suffisante pour être ressentie comme douloureuse, il ne sera pas la cause de votre mort. Si l’on tient compte de la résistance de l’air, un centime ne peut physiquement atteindre une vitesse suffisante pour porter un coup fatal. Même si les scientifiques ne peuvent pas, d’un point de vue éthique, mener des études où ils laissent tomber des centimes pour voir si des gens en meurent, la physique semble suffisamment solide pour me permettre de ne pas rejeter mon hypothèse nulle. Donc, la prochaine fois que vous vous promènerez dans la ville de New York, n’ayez pas peur des centimes qui tombent – ils ne mordront pas.
0 commentaire