Too big to write but not too big for Graham

Recentemente, quando estávamos a escrever o nosso livro Numericon, deparámo-nos com o que se tornou agora um dos nossos números favoritos: O número de Graham. Uma das razões pelas quais o adoramos é que este número é grande. Na verdade, isso é um eufemismo. O número de Graham’s é enorme.

p>O Universo observável é grande, mas o número de Graham é maior. Imagem: ESA e a Colaboração Planck.

O nosso novo número favorito é maior do que a idade do Universo, quer seja medido em anos (aproximadamente 14 mil milhões de anos) ou segundos (4,343×1017 segundos). É maior do que o número de Avogadro, um tamanho de 6,02214129 x 1023. Este é o número de átomos de hidrogénio em 1 grama de hidrogénio, que se chama uma toupeira e é a unidade padrão para medir uma quantidade de uma substância em química ou física.

O número de Graham é maior o número de átomos no Universo observável, que se pensa estar entre 1078 e 1082. É maior do que o 48º prime Mersenne,

o maior número prime que conhecemos, que tem um impressionante número de 17.425.170 dígitos. E é maior do que o famoso googol, 10100 (um 1 seguido de 100 zeros), que foi definido em 1929 pelo matemático americano Edward Kasner e nomeado pelo seu sobrinho de nove anos, Milton Sirotta. (Isto pode soar familiar, uma vez que o Google recebeu o nome deste número, embora se tenham enganado na ortografia).

O número de Graham é também maior que um googolplex, que Milton definiu inicialmente como 1, seguido por escrever zeros até se cansar, mas é agora comummente aceite como 10googol=10(10100). Um googleplex é significativamente maior do que o 48º Mersenne prime. Você, ou melhor, um computador, pode escrever o 48º Mersenne prime na sua totalidade, todos os 17,425,170 dígitos do mesmo. Mas, apesar de poder dizer-vos o que é qualquer dígito no googolplex (o primeiro é um 1, os restantes são todos 0), nenhuma pessoa, nenhum computador, nenhuma civilização será capaz de o escrever por completo. Isto é porque não há espaço suficiente no Universo para escrever todos os dígitos do googol+1 de um googolplex. Como Kasner, e o seu colega James Newman, disseram sobre o googolplex (no seu maravilhoso livro de 1940 Mathematics and the imagination which introduced the world to these numbers): “Terá uma ideia do tamanho deste número muito grande mas finito pelo facto de que não haveria espaço suficiente para o escrever, se fosse até à estrela mais distante, percorrendo todas as nebulosas e colocando zeros a cada centímetro do caminho”.

O número de Graham é maior do que o googolplex. É tão grande, que o Universo não contém material suficiente para escrever os seus dígitos: é literalmente demasiado grande para escrever. Mas este número é finito, é também um número inteiro, e apesar de ser tão grande que sabemos que é divisível por 3 e termina num 7.

Uma grande festa

As origens do número de Graham remontam a 1928 quando um brilhante jovem matemático, Frank Ramsey, notou uma coisa surpreendente quando estava a trabalhar num artigo sobre lógica: a desordem completa parecia ser impossível. Por mais complicado que o seu sistema pareça, bolsos de qualquer tamanho são sempre garantidos se o sistema for suficientemente grande.

Este resultado, que era apenas uma pequena parte do papel em que ele estava a trabalhar, foi o início de todo um novo campo da matemática chamado Teoria Ramsey. Esta área da matemática é muitas vezes explicada com o exemplo de uma festa. Suponha que está a dar uma festa e quer ter a certeza de que convida uma boa mistura de pessoas e decide manter um registo de quem sabe quem. Suponha que desenha um mapa das relações de todos os seus amigos, ligando duas pessoas com uma borda azul se forem amigos e com uma borda vermelha se forem estranhos. Então poderá acabar com algo do género:

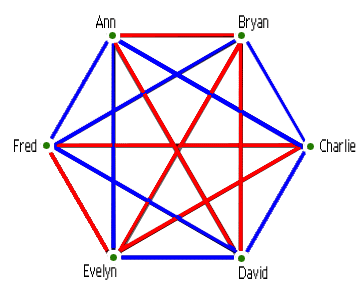
Agora isto parece bastante complicado e seria necessária muita informação para descrever quem está ligado por arestas vermelhas e quem está ligado por arestas azuis. Mas se se fizer zoom apenas em Ann, Bryan e David, todos eles estão unidos por bordas vermelhas. Este triângulo vermelho é um exemplo de ordem escondida na rede global confusa. Quanto mais ordenado for um sistema, mais simples é a sua descrição. A rede de amizade mais ordenada é aquela que tem todas as arestas da mesma cor: ou seja, todos são amigos ou todos são estranhos.

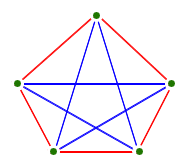
Ramsey descobriu que por mais ordem que procurasse – quer fossem três pessoas que fossem todas amigas e estranhas ou vinte pessoas que fossem todas amigas e estranhas – tinha a certeza de a encontrar desde que o sistema que procurava fosse suficientemente grande. Para garantir a si próprio um grupo de três pessoas que são todas amigas ou todas estranhas, precisa de uma rede de amizade de seis pessoas: cinco pessoas não é suficiente, como este contra-exemplo mostra.

O número de pessoas de que precisa para garantir que encontrará três amigos ou três estranhos chama-se Ramsey número R(3,3). Conhecemos alguns números Ramsey: vimos que R(3,3)=6, e foi provado que R(4,4), o número de pessoas de que precisa para garantir que encontrará quatro amigos ou quatro estranhos, é 18. Mas atingimos uma parede muito rapidamente. Por exemplo, não sabemos o que é R(5,5). Sabemos que está algures entre 43 e 49, mas isso é o mais próximo que podemos chegar por agora.

Parte do problema é que os números na teoria de Ramsey crescem incrivelmente grandes muito rapidamente. Se olharmos para as relações entre três pessoas, a nossa rede tem apenas três arestas e há 23 maneiras razoáveis de colorir a rede. Para quatro pessoas há seis arestas e 26=64 possíveis colorações. Mas para as relações entre seis pessoas, existem quinze arestas e já temos de considerar um possível colorido de 215=32,768. Os matemáticos estão bastante certos de que R(5,5) é igual a 43 mas ainda não encontraram uma forma de o provar. Uma opção seria verificar todos os corantes possíveis para uma rede de 43 pessoas. Mas cada uma destas tem 903 arestas, pelo que teria de verificar todas as 2903 colorações possíveis – mais colorações do que há átomos no Universo observável!

Muito grande para escrever mas não demasiado grande para Graham

Os números grandes sempre fizeram parte da teoria de Ramsey, mas em 1971 o matemático Ronald Graham inventou um número que anulou tudo antes dele. Ele estabeleceu um limite superior para um problema na área que era, na altura, o maior número explicitamente definido alguma vez publicado. Em vez de desenhar redes das relações entre as pessoas num pedaço de papel plano como temos feito até agora, Graham estava interessado em redes nas quais as pessoas estavam sentadas nos cantos de um cubo.

Nesta imagem podemos ver que para uma determinada fatia plana diagonal através do cubo, uma que contém quatro dos cantos, todas as arestas são vermelhas. Mas nem todas as colorações de um cubo tridimensional têm uma fatia de tal cor única. Felizmente, porém, os matemáticos também têm uma forma de pensar em cubos de dimensão superior. Quanto maior a dimensão, mais cantos há: um cubo tridimensional tem 8 cantos, um cubo tetradimensional tem 16 cantos, um cubo quadridimensional tem 32 cantos e assim por diante. Graham queria saber quão grande tinha de ser a dimensão do cubo para garantir a existência de uma única fatia colorida.

p>Ronald Graham que nos deu o seu belo número. Imagem: Cheryl Graham.

Graham conseguiu encontrar um número que garantiu a existência de tal fatia para um cubo dessa dimensão. Mas este número, como mencionámos anteriormente, era absolutamente maciço, tão grande que é demasiado grande para escrever dentro do Universo observável. Graham foi, contudo, capaz de definir explicitamente este número usando uma notação engenhosa chamada up-arrow notation que alarga as nossas operações aritméticas comuns de adição, multiplicação e exponenciação.

Podemos pensar na multiplicação como adição repetida:

Se definirmos a operação de seta única, , a ser exponenciação, assim:

então podemos definir a operação de dupla fila a ser

Podemos continuar a construir novas operações, repetindo as anteriores. A próxima seria a tripla linha

uma torre de potências de 3 que é 7.625.597.484.987 níveis elevados! (Ver aqui para ler sobre a notação de up-arrow com mais detalhes)

O número que passou a ser conhecido como o número de Graham (não o número exacto que apareceu no seu trabalho inicial, é um número ligeiramente maior e ligeiramente mais fácil de definir que ele explicou a Martin Gardner pouco tempo depois) é definido usando esta notação de up-arrow, num processo cumulativo que cria torres de potências de três que rapidamente espiralam para além de qualquer magnitudes que possamos imaginar.

Mas o que gostamos no número de Graham’s é que esta quantidade inimaginavelmente grande não é um conceito teórico: é um número exacto. Sabemos que é um número inteiro, na verdade é fácil ver que este número é um múltiplo de três devido à forma como é definido como uma torre de poderes de três. E os matemáticos aprenderam muito sobre os processos utilizados para definir o número de Graham’s, incluindo o facto de que uma vez que uma torre de potências é suficientemente alta, os dígitos decimais mais à direita permanecerão eventualmente os mesmos, não importa quantos mais níveis se acrescente à torre de potências. O número de Graham’s pode ser demasiado grande para escrever, mas sabemos que termina em sete. A matemática tem o poder não só de definir o inimaginável, mas também de o investigar.

Sobre este artigo

Rachel Thomas e Marianne Freiberger são os editores de Plus. Este artigo é um extracto editado do seu novo livro Numericon: Uma viagem através das vidas ocultas dos números.