- Definir meia-vida.
- Determinar a quantidade de substância radioactiva remanescente após um dado número de meia-vidas.
Se um dado isótopo é ou não radioactivo é uma característica desse isótopo em particular. Alguns isótopos são estáveis indefinidamente, enquanto outros são radioactivos e decaem através de uma forma característica de emissão. Com o passar do tempo, cada vez menos isótopo radioactivo estará presente, e o nível de radioactividade decresce. Um aspecto interessante e útil do decaimento radioactivo é a meia-vida, que é a quantidade de tempo que leva a metade de um isótopo radioactivo a decair. A meia-vida de um isótopo radioactivo específico é constante; não é afectada pelas coTndições e é independente da quantidade inicial desse isótopo.
Considere o seguinte exemplo. Suponha-se que temos 100,0 g de trítio (um isótopo radioactivo de hidrogénio). Tem uma meia-vida de 12,3 y. Após 12,3 y, metade da amostra terá decaído de hidrogénio-3 para hélio-3, emitindo uma partícula beta, de modo que apenas 50,0 g do trítio original permanece. Depois de mais 12,3 y, um total de 24,6 y – outra metade do trítio restante terá decaído, deixando 25,0 g de trítio. Após mais 12,3 y – agora um total de 36,9 y – outra metade do trítio restante terá decaído, deixando 12,5 g. Esta sequência de eventos é ilustrada na Figura 15.1 “Decadência radioactiva”.
Figure 15.1 Decadência Radioactiva
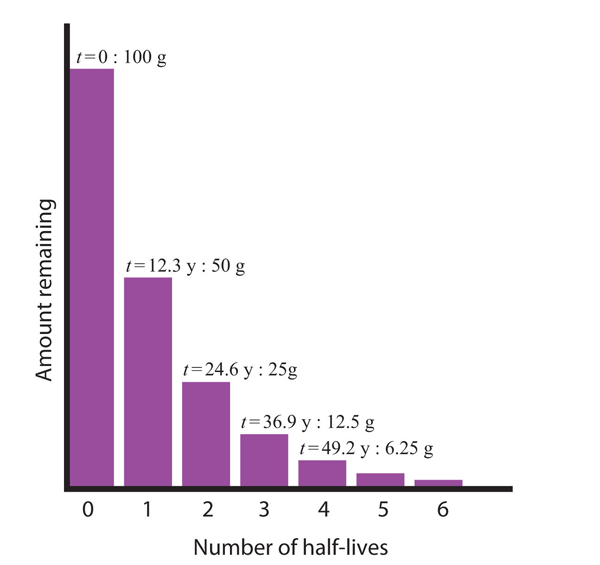
Durante cada meia-vida sucessiva, metade da quantidade inicial irá decair radioactivamente.
Podemos determinar a quantidade de um isótopo radioactivo restante após um determinado número de semi-vidas, utilizando a seguinte expressão:
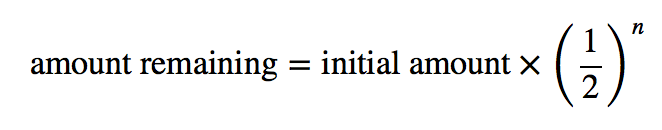
onde n é o número de semi-vidas. Esta expressão funciona melhor quando o número de meias-vidas é um número inteiro.
Exemplo 3
A meia-vida do flúor-20 é 11,0 s. Se uma amostra contém inicialmente 5,00 g de flúor-20, quanto resta após 44.0 s?
Solução
Se compararmos o tempo que passou com a meia-vida do isótopo, notamos que 44,0 s é exactamente 4 meia-vida, portanto, usando a expressão anterior, n = 4. Substituindo e resolvendo resultados no seguinte:

Menos de um terço de um grama de restos de flúor-20.
Teste-te
A meia-vida do titânio-44 é de 60,0 y. Uma amostra de titânio contém 0,600 g de titânio-44. Quanto resta após 240,0 y?
Resposta
0,0375 g
Metade de vida dos isótopos varia de fracções de um microssegundo a milhares de milhões de anos. A tabela 15.2 “Meias-vidas de vários isótopos” lista as meias-vidas de alguns isótopos.
Tabela 15.2 Meias-vidas de vários isótopos
| Isotope | Half-Life |
|---|---|
| 3H | 12.3 y |
| 5730 y | |
| 1,26 × 109 y | |
| 29,1 y | |
| 8,04 d | |
| 222Rn | 3.823 d |
| 235U | 7,04 × 108 y |
| 238U | 4.47 × 109 y |
| 241Am | 432,7 y |
| 248Bk | 23.7 h |
| 4 ms |
Chemistry Is Everywhere: Elementos Radioactivos no Corpo
Pode não pensar em si próprio como radioactivo, mas está. Uma pequena porção de certos elementos do corpo humano são radioactivos e estão constantemente em decadência. O quadro seguinte resume a radioactividade no corpo humano normal.
| Radioactive Isotope | Half-Vida (y) | ||
|---|---|---|---|
| 40K | 1.26 × 109 | 0.0164 | 4,340 |
| 14C | 5,730 | 1.6 × 10-8 | 3.080 |
| 4,9 × 1010 | 600 | ||
| 210Pb | 22.3 | 5,4 × 10-10 | 15 |
| 3H | 12,3 | 2 × 10-14 | 7 |
| 4.47 × 109 | 1 × 10-4 | 5 | |
| 5,76 | 4,6 × 10-14 | 5 | |
| 1.620 | 3.6 × 10-11 | 3 |
O corpo humano médio experimenta cerca de 8.000 decaimentos radioactivos/s.
A maior parte da radioactividade no corpo humano provém do potássio-40 e do carbono-14. O potássio e o carbono são dois elementos sem os quais não podemos absolutamente viver, por isso, a menos que possamos remover todos os isótopos radioactivos destes elementos, não há forma de escapar pelo menos a alguma radioactividade. Há debate sobre qual o elemento radioactivo mais problemático. Há mais potássio-40 no corpo do que o carbono-14, e tem uma semi-vida muito mais longa. O potássio-40 também se decompõe com cerca de 10 vezes mais energia do que o carbono-14, tornando cada decomposição potencialmente mais problemática. Contudo, o carbono é o elemento que constitui a espinha dorsal da maioria das moléculas vivas, tornando mais provável que o carbono-14 esteja presente em torno de moléculas importantes, tais como proteínas e moléculas de ADN. A maioria dos especialistas concorda que embora seja imprudente esperar absolutamente nenhuma exposição à radioactividade, podemos e devemos minimizar a exposição ao excesso de radioactividade.
E se o tempo decorrido não for um número exacto de meias-vidas? Ainda podemos calcular a quantidade de material que nos resta, mas a equação é mais complicada. A equação é
onde e é a base dos logaritmos naturais (2.71828182…), t é o tempo decorrido, e t1/2 é a meia-vida do isótopo radioactivo. As variáveis t e t1/2 devem ter as mesmas unidades de tempo, e pode ser necessário certificar-se de que sabe como avaliar os poderes do logaritmo natural na sua calculadora (para muitas calculadoras, existe uma função “logaritmo inverso” que pode utilizar; consulte o seu instrutor se não tiver a certeza de como utilizar a sua calculadora). Embora esta seja uma fórmula mais complicada, o tempo t não precisa de ser um múltiplo exacto de meia-vida.
Exemplo 4
A meia-vida do flúor-20 é 11,0 s. Se uma amostra contém inicialmente 5,00 g de flúor-20, quanto resta após 60,0 s?
Solução
P>Embora semelhante ao Exemplo 3, a quantidade de tempo não é um múltiplo exacto de meia-vida. Aqui identificamos a quantidade inicial como 5,00 g, t = 60,0 s, e t1/2 = 11,0 s. Substituindo na equação:
quantidade restante = (5,00 g) × e-(0,693)(60,0 s)/11,0 s
avaliação do expoente (e notando que as unidades s cancelam), obtemos
quantidade restante = (5.00 g) × e-3,78
Solvendo, a quantidade restante é 0,114 g. (Pode querer verificar esta resposta para confirmar que está a usar a sua calculadora correctamente.)
Teste a si mesmo
A meia-vida do titânio-44 é 60,0 y. Uma amostra de titânio contém 0,600 g de titânio-44. Quanto resta após 100,0 y?
Resposta
0,189 g
Key Takeaways
- Processos radioactivos naturais são caracterizados por uma meia-vida, o tempo que leva para que metade do material se decomponha radioactivamente.
- A quantidade de material restante após um certo número de meia-vida pode ser facilmente calculada.
Exercícios
-
Todos os isótopos têm uma meia-vida? Explique a sua resposta.
Quem é mais radioactivo – um isótopo com uma meia-vida longa ou um isótopo com uma meia-vida curta?
Quanto tempo demora 1,00 g de paládio-103 a decair até 0,125 g se a sua meia-vida for 17,0 d?
Quanto tempo demora 2.00 g de nióbio-94 a decair para 0,0625 g se a sua meia-vida for 20,000 y?Levou 75 y para 10,0 g de um isótopo radioactivo a decair para 1.25 g. Qual é a meia-vida deste isótopo?
Levou 49,2 s para 3.000 g de um isótopo radioactivo a decair para 0,1875 g. Qual é a semi-vida deste isótopo?
A semi-vida de americium-241 é de 432 y. Se 0,0002 g de americium-241 estiver presente num detector de fumo na data de fabrico, que massa de americium-241 está presente após 100,0 y? Após 1.000,0 y?
Se a meia-vida do trítio (hidrogénio-3) for de 12,3 y, quanto de uma amostra de 0,00444 g de trítio está presente após 5,0 y? Após 250,0 y?
Explicar porque é que a quantidade restante após 1.000,0 y no Exercício 7 não é um décimo da quantidade presente após 100,0 y, apesar do facto de a quantidade de tempo decorrido ser 10 vezes maior.
Explicar porque é que a quantidade restante após 250,0 y.0 y no Exercício 8 não é um quinto da quantidade presente após 5,0 y, apesar de a quantidade de tempo decorrido ser 50 vezes maior.
Um artefacto contendo carbono-14 contém 8,4 × 10-9 g de carbono-14. Se a idade do artefacto é 10,670 y, qual a quantidade de carbono-14 que continha originalmente? A meia-vida do carbono-14 é 5.730 y.
Carbon-11 é um isótopo radioactivo utilizado em tomografia por emissão de positrões (PET) para diagnóstico médico. A emissão de positrões é outro tipo, embora raro, de radioactividade. A meia-vida do carbono-11 é de 20,3 min. Se 4,23 × 10-6 g de carbono-11 for deixado no corpo após 4,00 h, que massa de carbono-11 estava presente inicialmente?
Respostas
Apenas isótopos radioactivos têm uma meia-vida.
p>51.0 d
25 y
0.000170 g; 0.0000402 g
Desintegração radioactiva é um processo exponencial, não um processo linear.
3.1 × 10-8 g
0 comentários