Um procedimento passo a passo para usar o teste F
Para atingir os objectivos acima referidos, seguiremos estes passos:
- Formular a estatística do teste F, também conhecido como o teste F.
- Identificar a Função de Densidade de Probabilidade da variável aleatória que a estatística F representa sob a suposição de que a hipótese nula é verdadeira.
- Plugar os valores na fórmula para a estatística F e calcular o valor de probabilidade correspondente utilizando a Função de Densidade de Probabilidade encontrada no passo 2. Esta é a probabilidade de observar o valor da estatística F assumindo que a hipótese nula é verdadeira.
- Se a probabilidade encontrada no passo 3 for inferior ao limiar de erro, tal como 0,05, rejeitar a hipótese nula e aceitar a hipótese alternativa a um nível de confiança de (1,0 – limiar de erro), por exemplo 1-0,05 = 0,95 (ou seja, 95% de nível de confiança). Caso contrário, aceitar a hipótese nula com uma probabilidade de erro igual ao limiar de erro, por exemplo a 0,05 ou 5%.
p>Divergir para estes passos.
STEP 1: Desenvolver a intuição para a estatística do teste
Recolher que o teste F mede o quanto melhor um modelo complexo é em comparação com uma versão mais simples do mesmo modelo na sua capacidade de explicar a variância na variável dependente.
Considerar dois modelos de regressão 1 e 2:
- Let Modelo 1 tem parâmetros k_1. O Modelo 2 tem parâmetros k_2.
- li>Let k_1 < k_2
- li> Assim, o Modelo 1 é a versão mais simples do modelo 2. ou seja, o modelo 1 é o modelo restrito e o modelo 2 é o modelo sem restrições. O modelo 1 pode ser aninhado dentro do modelo 2.
- Leve RSS_1 e RSS_2 ser a soma dos quadrados de erros residuais depois de o modelo 1 e o modelo 2 serem ajustados ao mesmo conjunto de dados.
- Leve n ser o número de amostras de dados.
Com as definições acima, a estatística de teste do teste F para regressão pode ser expressa como uma relação como se segue:

A fórmula estatística F permite calcular quanto da variância na variável dependente, o modelo mais simples não é capaz de explicar, em comparação com o modelo complexo, expresso como uma fracção da variação inexplicável do modelo complexo.
Na análise de regressão, o erro quadrático médio do modelo ajustado é uma excelente medida da variância inexplicada. O que explica os termos RSS no numerador e no denominador.
O numerador e o denominador são adequadamente escalados utilizando os correspondentes graus de liberdade disponíveis.
A própria estatística F é uma variável aleatória.
Determinemos qual a Função de Densidade de Probabilidade que a estatística F obedece.
STEP 2: Identificação da Função de Densidade de Probabilidade da estatística F
Nota que tanto o numerador como o denominador da estatística de teste contêm somas de quadrados de erros residuais. Recordar também que na regressão, um erro residual é uma variável aleatória com alguma função de densidade de probabilidade (ou massa de probabilidade), ou seja, um PDF ou PMF, dependendo se é contínuo ou discreto. Neste caso, estamos preocupados em encontrar o PDF da estatística F.
Se assumirmos que os erros residuais dos dois modelos são 1) independentes e 2) normalmente distribuídos, que por acaso são requisitos da regressão dos Mínimos Quadrados Ordinários, então pode-se ver que o numerador e denominador da fórmula da estatística F contém somas de quadrados de variáveis aleatórias independentes, normalmente distribuídas.
É possível provar que a soma dos quadrados de k variáveis aleatórias normais e independentes seguem o PDF da distribuição do Qui-quadrado(k).

Assim, o numerador e denominador da fórmula F-estatística pode ser mostrado a cada uma das versões em escala de duas distribuições chi-quadrado.
Com um pouco de matemática, também se pode mostrar que a proporção de duas variáveis aleatórias distribuídas ao qui-quadrado devidamente escalonadas é ela própria uma variável aleatória que segue a distribuição de F, cujo PDF é mostrado abaixo.
 A-distribuição F
A-distribuição F
Por outras palavras:
se a variável aleatória X tiver o PDF da distribuição F com os parâmetros d_1 e d_2, ou seja :
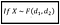
then, X pode ser demonstrado ser expresso como a razão de duas variáveis aleatórias devidamente escalonadas X_1 e X_2, cada uma das quais tem o PDF de uma distribuição de Chi-quadrado. i.e. :

p>Agora recorde-se que k_1 e k_2 são o número de variáveis nos modelos simples e complexos M1 e M2 introduzidos anteriormente, e n é o número de amostras de dados.
Substituto d_1 e d_2, como se segue:
d_1 = (k_2 – k_1) que é a diferença em graus de liberdade dos resíduos dos dois modelos M1 e M2 a comparar, e
d_2 = (n – k_2) que é os graus de liberdade dos resíduos do modelo complexo M2,
Com estas substituições, podemos reescrever a fórmula da distribuição F como se segue:

p>Vamos comparar a fórmula acima com a fórmula para a estatística F (reproduzida abaixo), onde sabemos que o numerador e denominador contêm PDFs com escala adequada de distribuições de Chi-quadrado:

Comparando estas duas fórmulas, é evidente que:
- O grau de liberdade ‘a’ da distribuição do Chi-quadrado no numerador é (k1 – k2).
- O grau de liberdade ‘b’ da distribuição Qui-quadrado no denominador é (n – k2).
- A estatística de teste do teste F tem o mesmo PDF que a da distribuição F.
Por outras palavras, a estatística F segue a distribuição F.
STEP 3: Cálculo do valor da estatística F
Se utilizar o estimador OLS do statsmodels, este passo é uma operação de uma linha. Basta imprimir OLSResults.summary() e obterá:
- O valor da estatística F e,
- O valor ‘p’ correspondente, ou seja, a probabilidade de encontrar este valor, a partir do PDF da distribuição F.
A biblioteca de modelos de estatísticas fará o trabalho grunhido de ambos os cálculos.
print(ols_results.summary())
Isto imprime o seguinte:
STEP 4: Determinar se a hipótese nula pode ser aceite
Desde OLSResultados.resumo() imprime a probabilidade de ocorrência da estatística F sob a hipótese de que a hipótese nula é verdadeira, só precisamos de comparar esta probabilidade com o nosso valor limiar alfa. No nosso exemplo, o valor p devolvido por .summary() é 4,84E-16, o que é um número extremamente pequeno. Muito menor do que mesmo alfa = 0,01. Assim, há muito menos de 1% de probabilidade de a estatística F de 136,7 poder ter ocorrido por acaso sob a hipótese de uma hipótese Nula válida.
Assim, rejeitamos a hipótese Nula e aceitamos a hipótese alternativa H_1 de que o modelo complexo, isto é, o modelo de variável desfasada, apesar das suas falhas óbvias, é capaz de explicar melhor a variância da variável dependente Preço de fecho do que o modelo apenas de intercepção.
0 comentários