Integers e números inteiros parecem significar a mesma coisa mas na realidade, uma vez que, os dois termos são diferentes. Por esta razão, muitos estudantes ficam perplexos quando encontram problemas envolvendo inteiros e números inteiros.
Neste artigo, vamos aprender sobre inteiros e números inteiros. Após esta discussão, não cometerão mais erros quando usarem números inteiros e números inteiros.
O que é um Inteiro?
Em Matemática, os números inteiros são conjuntos de números inteiros, incluindo números positivos, negativos e números zero geralmente representados pelo símbolo ‘Zahlen’ Z= {…, -4, -3, -2, -1,0,1,2,3, 4…}. Note-se que um número inteiro nunca pode ser uma fracção, uma decimal ou um por cento.
Por outro lado, números inteiros são um conjunto de números positivos e zero sem um ponto decimal ou fracções, números inteiros são representados como W = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9……………}.
Da definição acima de números inteiros e inteiros, pode-se notar que, todos os números inteiros são inteiros mas nem todos os inteiros são números inteiros. Em suma, os números inteiros são compostos por números negativos, positivos e zero, enquanto que os números inteiros são compostos apenas por números positivos e zero. Portanto, números inteiros estão contidos em números inteiros.
Se ainda tiver dúvidas, o que são um número inteiro e um número inteiro? Então, o fluxograma abaixo dar-lhe-á uma compreensão mais abrangente.
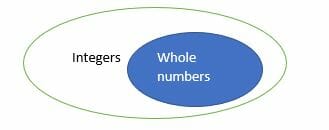
Existem três tipos de números inteiros, nomeadamente:
- Números positivos
- Números negativos
- O zero
Números positivos são números inteiros com um sinal de mais (+) na frente do valor numérico. Na maioria dos casos, o sinal de mais é ignorado simplesmente representado sem o símbolo. Os números positivos são maiores do que os números negativos, bem como um zero. Os números positivos são representados à direita do zero na linha numérica.
Exemplos de números positivos são: 1,2, 88, 800,9900, etc.
Números negativos são simbolizados com um traço ou sinal de menos em frente do valor numérico. Estes números são representados na linha de números à esquerda da origem. Exemplos de números negativos são: …., – 800, -100, -10, -2, -1.
Zero é um número neutro na linha numérica. Não é nem positivo nem negativo.
Números inteiros
Números inteiros possuem muitas propriedades. Estas propriedades baseiam-se em operações tais como adicionar, subtrair, dividir e multiplicar.
Por exemplo, a soma de dois números inteiros é sempre um todo. No entanto, a subtracção de dois números inteiros pode resultar num número inteiro.
Multiplicação de dois números inteiros resulta num número inteiro. A divisão no outro pode não resultar em obter uma fracção ou um número inteiro.
p>Agora vejamos algumas das propriedades dos números inteiros:
- li>Propriedade de encerramento/ul>
- Identidade aditiva
- Identidade multiplicativa
- Propriedade Associativa
- Propriedade Distributiva de números inteiros
- Multiplicação por zero
- Divisão de um número inteiro por zero
A propriedade de encerramento de adição e multiplicação implica, se x e y são números inteiros, então o produto x * y e a soma x + y é também um número inteiro.
- Propriedade de adição
Se x e y são números inteiros; x + y = y + x e x * y=y * x
Adição de zero a um número inteiro deixa o número inalterado; y + 0 = y
Multiplicação de um número inteiro por 1 deixa o número inalterado; se x for um número inteiro, então x * 1 = x
X + (y + z) = (x + y) + z e x * (y z) = (x y) z
x * (y + z) = (x y) + (x z) e x * (y-z) = (x y)- (x z)
Se x for um número inteiro então; x * 0 = 0
Se x é um número inteiro; então x/0 = indefinido.
Aplicações de Integers
Integers e números inteiros são amplamente aplicados em diferentes campos. Por exemplo, os números inteiros são utilizados para definir a população de um dado grupo de quantidades. A população nunca pode ser negativa e por isso são utilizados números inteiros.
No sector bancário, os inteiros são utilizados para denotar um débito ou um crédito.
Integer são também utilizados para descrever a temperatura de um corpo quer abaixo ou acima de zero centígrado. Os inteiros são também aplicados no desporto para mostrar diferenças de objectivos.
br>>
h4>Lição anterior | Página principal | Lição seguinte
0 comentários