Leonhard Euler, 1707 – 1783
Comecemos por apresentar o protagonista desta história – a fórmula de Euler:
Simples embora possa parecer, esta pequena fórmula encapsula uma propriedade fundamental daqueles sólidos tridimensionais a que chamamos poliedros, que fascinam os matemáticos há mais de 4000 anos. Na verdade, posso ir mais longe e dizer que a fórmula de Euler nos diz algo muito profundo sobre a forma e o espaço. A fórmula tem o nome do famoso matemático suíço Leonhard Euler (1707 – 1783), que teria celebrado o seu 300º aniversário este ano.
O que é um poliedro?
Antes de examinarmos o que a fórmula de Euler nos diz, vejamos o poliedro com um pouco mais de detalhe. Um poliedro é um objecto sólido cuja superfície é constituída por um número de faces planas que, por sua vez, são delimitadas por linhas rectas. Cada face é de facto um polígono, uma forma fechada no plano plano bidimensional plano composta por pontos unidos por linhas rectas.
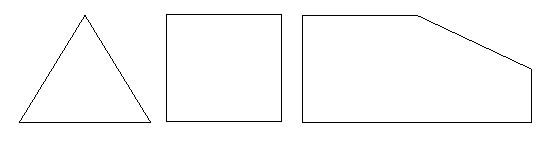
Figure 1: O triângulo e o quadrado familiares são ambos polígonos, mas os polígonos também podem ter formas mais irregulares como a que aparece à direita.
P>Polígonos não podem ter buracos, como ilustra a figura abaixo: a forma à esquerda aqui é um polígono, enquanto que a forma à direita não é.
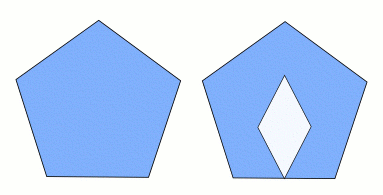
Figure 2: A forma à esquerda é um polígono, mas a da direita não é, porque tem um ‘buraco’.
Um polígono é chamado regular se todos os seus lados tiverem o mesmo comprimento, e todos os ângulos entre eles forem iguais; o triângulo e o quadrado na figura 1 e o pentágono na figura 2 são regulares.
Um poliedro é o que se obtém quando se move uma dimensão para cima. É um objecto fechado e sólido cuja superfície é constituída por um número de faces poligonais. Chamamos aos lados destas faces arestas – duas faces encontram-se ao longo de cada uma destas arestas. Chamamos os cantos dos vértices das faces, de modo a que qualquer vértice se encontre em pelo menos três faces diferentes. Para ilustrar isto, aqui estão dois exemplos do conhecido poliedro.
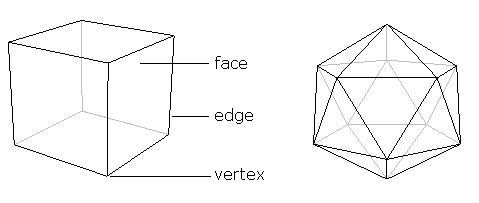
Figure 3: O cubo familiar à esquerda e o icosaedro à direita. Um poliedro consiste em faces poligonais, os seus lados são conhecidos como arestas, e os cantos como vértices.
Um poliedro consiste em apenas uma peça. Não pode, por exemplo, ser constituído por duas (ou mais) partes basicamente separadas unidas por apenas uma aresta ou um vértice. Isto significa que nenhum dos seguintes objectos é um verdadeiro poliedro.
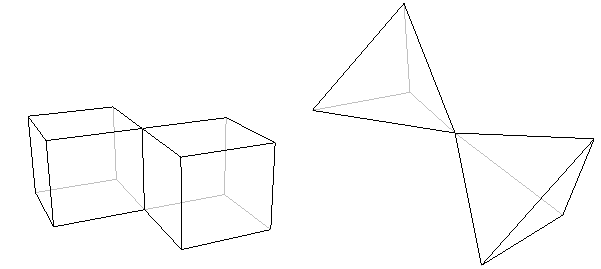
Figure 4: Estes objectos não são poliedros porque são constituídos por duas partes separadas que se encontram apenas numa borda (à esquerda) ou num vértice (à direita).
O que nos diz a fórmula?
Estamos agora prontos para ver o que a fórmula de Euler nos diz sobre poliedros. Olhe para um poliedro, por exemplo o cubo ou o icosaedro acima, conte o número de vértices que tem, e chame este número V. O cubo, por exemplo, tem 8 vértices, portanto V = 8. A seguir, conte o número de arestas que o poliedro tem, e chame este número E. O cubo tem 12 arestas, portanto no caso do cubo E = 12. Finalmente, contar o número de faces e chamar-lhe F. No caso do cubo, F = 6. Agora a fórmula de Euler diz-nos que
ou, em palavras: o número de vértices, menos o número de arestas, mais o número de faces, é igual a dois.
no caso do cubo, já vimos que V = 8, E = 12 e F = 6. Assim,
qual é o que a fórmula de Euler nos diz que deve ser. Se olharmos agora para o icosaedro, verificamos que V = 12, E = 30 e F = 20. Agora,
A fórmula do elogio é verdadeira para o cubo e o icosaedro. Acontece, de forma bastante bonita, que é verdade para praticamente todos os poliedros. Os únicos poliedros para os quais não funciona são aqueles que têm buracos como o mostrado na figura abaixo.
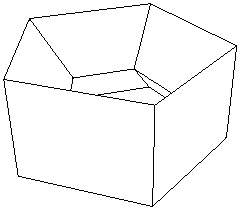
Figure 5: Este poliedro tem um furo que o atravessa. A fórmula de Euler não se mantém neste caso.
Estes poliedros são chamados não simples, em contraste com os que não têm furos, que são chamados simples. Os poliedros não-simples podem não ser os primeiros a surgir, mas existem muitos deles por aí, e não podemos fugir ao facto de a fórmula de Euler não funcionar para nenhum deles. Contudo, mesmo este facto embaraçoso tornou-se parte de toda uma nova teoria sobre espaço e forma.
O poder da fórmula de Euler
Sempre que os matemáticos se atiram a uma característica invariante, uma propriedade que é verdadeira para toda uma classe de objectos, eles sabem que estão em algo bom. Utilizam-no para investigar que propriedades pode ter um objecto individual e para identificar propriedades que todos eles devem ter. A fórmula de Euler pode dizer-nos, por exemplo, que não existe um poliedro simples com exactamente sete arestas. Não é preciso sentar-se com cartão, tesoura e cola para descobrir isto – a fórmula é tudo o que se precisa. O argumento mostrando que não existe poliedro de sete arestas é bastante simples, por isso dê uma vista de olhos se estiver interessado.
Usando a fórmula de Euler de forma semelhante podemos descobrir que não existe poliedro simples com dez faces e dezassete vértices. O prisma mostrado abaixo, que tem como base um octógono, tem dez faces, mas o número de vértices aqui é de dezasseis. A pirâmide, que tem uma base de 9 lados, também tem dez faces, mas tem dez vértices. Mas a fórmula de Euler diz-nos que nenhum poliedro simples tem exactamente dez faces e dezassete vértices.
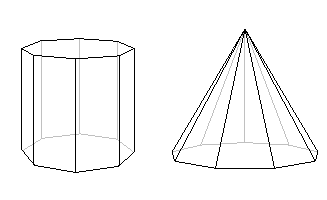p>Figure 6: Ambos estes poliedros têm dez faces, mas nenhum deles tem dezassete vértices. São considerações como estas que nos levam àquilo que é provavelmente a descoberta mais bela de todas. Trata-se dos Sólidos Platónicos, uma classe bem conhecida de poliedros com o nome do antigo filósofo grego Platão, em cujos escritos apareceram pela primeira vez.
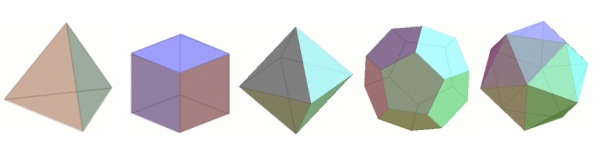
Figure 7: Os Sólidos Platónicos. Da esquerda para a direita temos o tetraedão com quatro faces, o cubo com seis faces, o octaedro com oito faces, o dodecaedro com doze faces, e o icosaedro com vinte faces.
Embora a sua elegância simétrica seja imediatamente visível quando se olha para os exemplos acima, não é de facto assim tão fácil fixá-lo em palavras. Acontece que é descrito por duas características. A primeira é que os sólidos platónicos não têm espigões ou mergulhos, pelo que a sua forma é agradável e arredondada. Por outras palavras, isto significa que sempre que escolher dois pontos num sólido platónico e desenhar uma linha recta entre eles, este pedaço de linha recta estará completamente contido dentro do sólido – um sólido platónico é o que se chama convexo. A segunda característica, chamada regularidade, é que todas as faces do sólido são polígonos regulares com exactamente o mesmo número de lados, e que o mesmo número de arestas sai de cada vértice do sólido.
O cubo é regular, uma vez que todas as suas faces são quadradas e exactamente três arestas saem de cada vértice. Pode verificar por si mesmo que o tetraedro, o octaedro, o icosaedro e o dodecaedro também são regulares.
Agora, pode perguntar-se quantos Sólidos Platónicos diferentes existem. Desde a descoberta do cubo e do tetraedro, os matemáticos foram tão atraídos pela elegância e simetria dos Sólidos Platónicos que procuraram mais, e tentaram listar todos eles. É aqui que entra a fórmula de Euler. Pode utilizá-la para encontrar todas as possibilidades para o número de rostos, arestas e vértices de um poliedro regular. O que irá descobrir é que existem de facto apenas cinco diferentes poliedros convexos regulares! Isto é muito surpreendente; afinal de contas, não há limite para o número de diferentes polígonos regulares, então porque devemos esperar um limite aqui? Os cinco sólidos platónicos são o tetraedro, o cubo, o octaedro, o icosaedro e o dodecaedro mostrados acima.
A prova
p>René Descartes,(1596 – 1650)
Jogar com vários poliedros simples mostrará que a fórmula de Euler é sempre verdadeira. Mas se for um matemático, isto não é suficiente. Vai querer uma prova, um argumento lógico à prova de água que lhe mostre que funciona realmente para todos os poliedros, incluindo os que nunca terá tempo de verificar.
Adrien-Marie Legendre, (1752 – 1833)
Apesar do nome da fórmula, não foi de facto Euler quem apresentou a primeira prova completa. A sua história é complexa, abrangendo 200 anos e envolvendo alguns dos maiores nomes da matemática, incluindo René Descartes (1596 – 1650), o próprio Euler, Adrien-Marie Legendre (1752 – 1833) e Augustin-Louis Cauchy (1789 – 1857).
Augustin-Louis Cauchy, (1789 – 1857)
É interessante notar que todos estes matemáticos utilizaram abordagens muito diferentes para provar a fórmula, cada uma delas surpreendente no seu engenho e perspicácia. É a prova de Cauchy, no entanto, que eu gostaria de lhe dar um sabor a isto. O seu método consiste em várias fases e etapas. A primeira etapa envolve a construção do que se chama uma rede.
Formar uma rede
Imagine que está a segurar o seu poliedro com uma face apontada para cima. Agora imagine “remover” apenas esta face, deixando para trás as arestas e vértices à sua volta, para que tenha uma “caixa” aberta. Em seguida, imagine que pode segurar a caixa e puxar as arestas da face em falta uma da outra. Se as puxar suficientemente longe, a caixa vai aplanar e tornar-se uma rede de pontos e linhas no plano plano. A série de diagramas abaixo ilustra este processo como aplicado a um cubo.
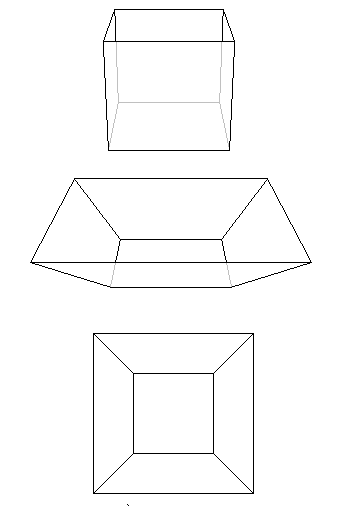p>Figure 8: Transformando o cubo em rede. Como pode ver no diagrama acima, cada face do poliedro torna-se uma área da rede rodeada por arestas, e isto é o que chamaremos uma face da rede. Estas são as faces interiores da rede. Há também uma face exterior que consiste na área fora da rede; isto corresponde à face que removemos do poliedro. Assim, a rede tem vértices, bordas rectas e faces poligonais.
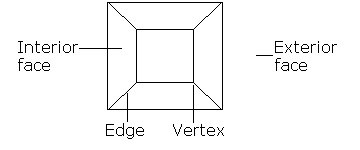
Figure 9: A rede tem faces, bordas e vértices.
Ao formar a rede não se adicionaram nem removeram quaisquer vértices, pelo que a rede tem o mesmo número de vértices que o poliedro – V. A rede também tem o mesmo número de arestas – E – que o poliedro. Agora para as faces; todas as faces do poliedro, excepto a “em falta”, aparecem “dentro” da rede. A face em falta tornou-se a face exterior que se estende ao longo de toda a rede. Assim, incluindo a face exterior, a rede tem faces F. Assim, pode utilizar a rede, em vez do próprio poliedro, para encontrar o valor de V – E + F. Vamos agora transformar a nossa rede para tornar este valor mais fácil de calcular.
Transformar a Rede
Existem três tipos de operações que podemos realizar na nossa rede. Vamos introduzir três passos que envolvem estes.
P>Passo 1 Começamos por olhar para as faces poligonais da rede e perguntamos: existe uma face com mais de três lados? Se houver, desenhamos uma diagonal como mostrado no diagrama abaixo, dividindo a face em duas faces menores.
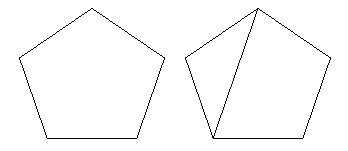p>Figure 10: Dividindo faces. Repetimos isto com a nossa face escolhida até que a face tenha sido dividida em triângulos.
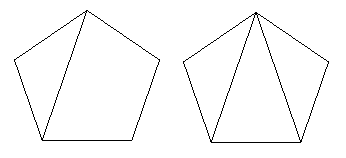
Figure 11: No final ficamos com faces triangulares.
Se houver uma outra face com mais de três lados, usamos o Passo 1 nessa face até que também ela tenha sido dividida em faces triangulares. Desta forma, podemos partir todas as faces em faces triangulares, e obtemos uma nova rede, cujas faces são todas triangulares. Ilustramos este processo mostrando como transformaríamos a rede que fizemos a partir de um cubo.
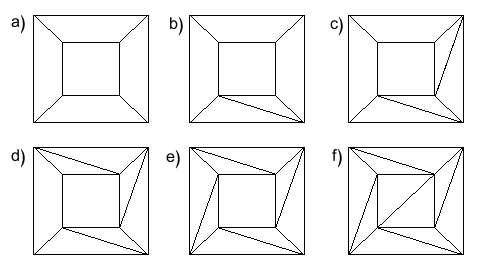
Figure 12: Isto é o que acontece com a rede do cubo à medida que executamos repetidamente o Passo 1.
Voltamos ao Passo 1, e olhamos para a rede que obtemos após executarmos o Passo 1 apenas uma vez. Agora, desenhando uma diagonal, adicionamos uma aresta. A nossa face original tornou-se em duas faces, por isso adicionámos uma ao número de faces. Não alterámos o número de vértices. A rede tem agora vértices V, bordas E + 1 e faces F + 1. Então como é que V – E + F mudou depois de termos realizado o Passo 1 uma vez? Usando o que sabemos sobre as mudanças em V, E e F, podemos ver que V – E + F se tornou V – (E + 1) + (F + 1). Agora temos
Então V – E + F não mudou depois do Passo 1! Porque cada uso do Passo 1 deixa V – E + F inalterado, continua inalterado quando chegamos à nossa nova rede composta inteiramente de triângulos! O efeito em V – E + F à medida que transformamos a rede feita a partir do cubo é mostrado na tabela abaixo.
| Round | V | E | F | V – E + F |
| (a) | 12 | 6 | 2 | |
| 8 | 13 | 7 | 2 | |
| (c) | 8 | 14 | 8 | 2 |
| (d) | 8 | 15 | 9 | 2 |
| (e) | 8 | 16 | 10 | 2 | (f) | 8 | 17 | 11 | 2 |
Agora introduzimos os Passos 2 e 3. Eles irão remover as faces do exterior da rede, reduzindo o número de faces passo a passo. Quando começarmos a fazer isto, a rede provavelmente já não representará um poliedro, mas a propriedade importante da rede é mantida.
P>Passo 2 Verificamos se a rede tem uma face que partilha apenas uma aresta com a face exterior. Se tiver, removemos esta face, removendo a única face partilhada. A área que tinha sido coberta pela nossa face escolhida torna-se parte da face exterior, e a rede tem um novo limite. Isto é ilustrado pelo diagrama abaixo para a rede feita a partir do cubo.
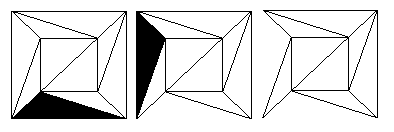p>Figure 13: Removendo faces com uma aresta externa. Agora, tomaremos V, E e F para serem os números de vértices, arestas e faces que a rede feita de faces triangulares tinha antes de executarmos o Passo 2. Analisamos agora como o número V – E + F mudou depois de executarmos uma vez o Passo 2. Removemos uma aresta, pelo que a nossa nova rede tem E – 1 arestas. Não tocámos em nada nos vértices, pelo que ainda temos os vértices V. A face que utilizámos para o Passo 2 foi fundida com a face exterior, pelo que agora temos F – 1 faces. Assim, V – E + F tornou-se V – (E – 1) + (F – 1) e
Então mais uma vez V – E + F não mudou.
P>Passo 3 Verificamos se a nossa rede tem uma face que partilha duas arestas com a face exterior. Se tiver, removemos esta face removendo ambas estas arestas partilhadas e o seu vértice partilhado, para que novamente a área pertencente à nossa face escolhida se torne parte da face exterior. Isto é ilustrado abaixo no caso da rede feita a partir do cubo, como é depois de executar o Passo 2 duas vezes.
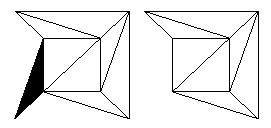p>Figure 14: Remoção de faces com duas arestas externas. Como fizemos antes, tomamos agora V, E e F para serem os números de vértices, arestas e faces da rede com que estamos a começar. Agora, como é que o número V – E + F foi afectado pelo Passo 3? Removemos um vértice – o que se encontra entre as duas arestas – por isso agora há V – 1 vértices. Removemos dois vértices, pelo que agora há E – 2 vértices. Finalmente, a nossa face escolhida fundiu-se com a face exterior, de modo que agora temos F – 1 faces. Assim V – E + F tornou-se (V – 1) – (E – 2) – (F – 1) e
Então mais uma vez V – E + F não mudou.
O segredo da prova reside em executar uma sequência de passos 2 e 3 para obter uma rede muito simples. Recorde-se que usámos repetidamente o Passo 1 para produzir uma rede com apenas faces triangulares. Esta rede terá definitivamente uma face que partilha exactamente uma aresta com a face exterior, por isso pegamos nesta face e executamos a Etapa 2. Podemos executar o Passo 2 em várias faces, uma de cada vez, até aparecer uma face que partilhe duas arestas com a face exterior. Podemos então executar a Etapa 3 utilizando esta face. Continuamos a executar as Etapas 2 e 3, e continuamos a remover as faces desta forma.
Existem duas regras importantes a seguir ao fazer isto. Em primeiro lugar, devemos sempre executar a Etapa 3 quando for possível fazê-lo; se houver uma escolha entre a Etapa 2 e a Etapa 3, devemos sempre escolher a Etapa 3. Se não o fizermos, a rede pode dividir-se em peças separadas. Em segundo lugar, só devemos remover faces uma de cada vez. Se não o fizermos, podemos acabar por ficar com as arestas a saltar sozinhas para a face exterior, e deixaremos de ter uma rede adequada. Para ilustrar o processo, vamos executar vários passos na rede do cubo, continuando de onde o deixámos no último diagrama.
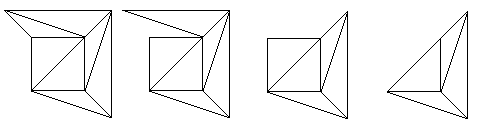
Figure 15: Aplicando o nosso algoritmo à rede do cubo.
Agora podemos fazer-nos uma ou duas perguntas. Será que este processo de remover caras alguma vez pára, e, se pára, com o que é que nos resta? Um pouco de consideração mostrar-vos-á que tem de parar – existem apenas finitamente muitas faces e arestas que podemos remover – e que, quando pára, ficamos com um único triângulo. Pode ver alguns diagramas descrevendo todo o processo para a rede formada a partir de um dodecaedro (lembre-se que este foi um dos sólidos platónicos introduzidos anteriormente).
Agora veja os números de vértices, arestas e faces presentes na nossa rede final – o triângulo único. Temos V=3, E=3, e F=2 – temos ainda de incluir a face exterior. Agora
Durante todo o processo, começando com o poliedro completo e terminando com um triângulo, o valor de V – E + F não mudou. Portanto, se V – E + F = 2 para a rede final, devemos também ter V – E + F = 2 para o próprio poliedro! A prova está completa!
Além do poliedro
I terminará mencionando algumas consequências da fórmula de Euler para além do mundo do poliedro. Vou começar com algo muito pequeno: chips de computador. Os chips de computador são circuitos integrados, compostos por milhões de componentes minúsculos ligados por milhões de pistas condutoras. Estes fazem lembrar as nossas redes acima, excepto que normalmente não é possível colocá-los num plano sem que algumas das pistas condutoras – as arestas – se cruzem. As travessias são uma coisa má na concepção dos circuitos, pelo que o seu número deve ser mantido em baixo, mas descobrir uma disposição adequada não é tarefa fácil. A fórmula do poliedro de Euler, com a sua informação sobre as redes, é um ingrediente essencial para encontrar soluções.
Agora passemos ao muito grande: o nosso universo. Até hoje, os cosmólogos ainda não concordaram com a sua forma exacta. Pivotal à sua consideração é a topologia, o estudo matemático da forma e do espaço. No século XIX, os matemáticos descobriram que todas as superfícies no espaço tridimensional são essencialmente caracterizadas pelo número de buracos que têm: o nosso poliedro simples não tem buracos, um donut tem um buraco, etc. A fórmula de Euler não funciona para poliedros com buracos, mas os matemáticos descobriram uma generalização excitante. Para qualquer poliedro, V – E + F é exactamente 2 menos 2 vezes o número de buracos! Acontece que este número, chamado a característica de Euler, é crucial para o estudo de todas as superfícies tridimensionais, e não apenas poliedros. A fórmula de Euler pode ser vista como o catalisador de toda uma nova forma de pensar a forma e o espaço.
Sobre o autor
Abi cresceu no norte de Inglaterra, e mudou-se para sul para estudar matemática no Imperial College, Londres, e Queen Mary, Universidade de Londres. Ela agora ensina matemática na Open University. O principal interesse matemático do Abi é a teoria do grupo. Ela gostou muito de explorar os mistérios da fórmula de Euler ao escrever este artigo.
Originalmente publicado em 1 de Junho de 2007
0 comentários