=================================================================================
Na teoria clássica da difracção, a difracção de Bragg ocorre quando partículas carregadas ou ondas de radiação electromagnética com um comprimento de onda comparável ao espaçamento atómico são incidentes a uma amostra cristalina. As ondas reflectidas nos centros de dispersão adjacentes devem ter uma diferença de trajectória igual a um número integral de comprimentos de onda. As ondas dispersas interferem de forma construtiva se permanecerem em fase. Portanto, a diferença de trajecto entre as ondas de electrões reflectidas dos planos superior e inferior na figura 3882 é igual ao comprimento total (AO+BO). Assumindo que os planos hkl estão espaçados a uma distância dhkl e a onda é incidente e reflectida nos ângulos θB, tanto AB como BC são iguais a dsin(θB) e a diferença total do caminho deve ser igual a 2dsin(θB).
Como discutido na página2678, podemos ter,
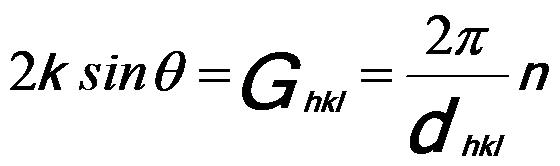 ——————————————
——————————————
where,
n — O múltiplo inteiro do menor Ghkl que é permitido,
k = λ/λ.
Por isso, podemos obter a conhecida condição de difracção de Bragg, dada por,
nλ = 2dhklsin(θB) ——————————————–
where,
n — Um inteiro, a ordem de reflexão;
dhkl — O espaçamento da malha de (hkl);
λ — O comprimento de onda da partícula carregada ou das ondas de radiação electromagnética;
θB — O ângulo de Bragg que é o ângulo entre o vector de onda incidente e os planos da malha como mostra a Figura 3882,
hkl — Índices Miller.
br> O ângulo de Bragg θB é um conceito muito importante na teoria da difracção, por exemplo, amplamente utilizado para explicar fenómenos de difracção de electrões e raios X. Intensidades muito fortes conhecidas como picos de Bragg são obtidas no padrão de difracção quando ondas dispersas satisfazem a condição de Bragg. O ângulo entre as ondas incidentes e reflectidas é igual a 2θB como mostrado na Figura 3882.
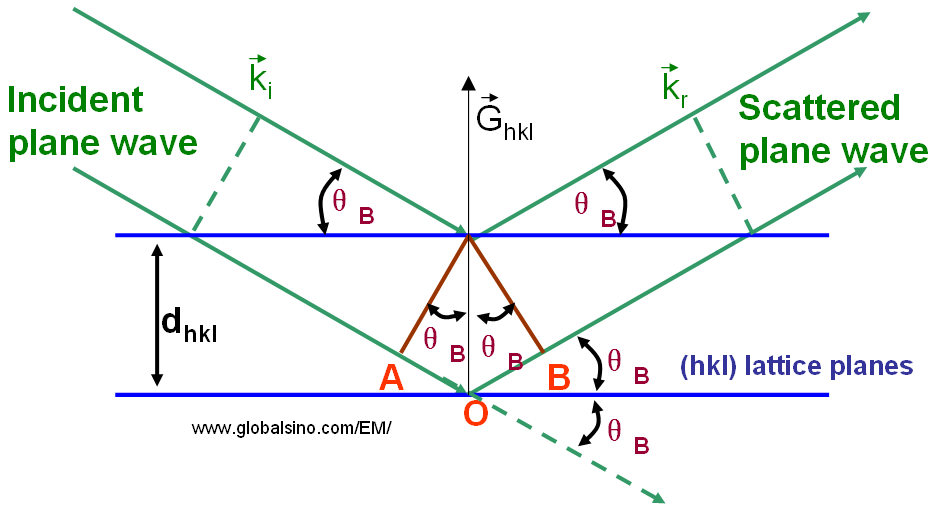
A diferença de caminho entre as ondas reflectidas é igual a AO + BO.
Para estruturas FCC e BCC, as constantes da malha são dadas por, (Pode descarregar o ficheiro excel para os seus próprios cálculos)
—————–
Tabela 3882a mostra que os electrões interagem com 1 electrão, muitos electrões, 1 núcleo, e muitos núcleos em sólidos.
| Interacção com electrão(s) | Interacção com núcleo/núcleo | |||||
|---|---|---|---|---|---|---|
| 1 electron | Muitos electrões | 1 núcleo | Muitos núcleos | |||
| Tipo de dispersão | Inelástico | Inelástico | Quasi-elástico | Elástico | Inelástico | |
| Efeito de dispersão | Efeito de Compton Electrónico; excitação de electrões (de 50 eV para alguns keV: EDS e EELS) | Excitação de lasmon (< 50 eV, ~100 nm TEM specimen); efeito Cerenkov | Rutherford scattering; phonon scattering (< 1 eV, calor) | Bragg scattering | Bremsstrahlung | |
Table 3882b lista alguns exemplos de ângulos de Bragg a várias tensões de feixe para o típico espaçamento d. Os ângulos de Bragg foram obtidos com a Equação 3882b (para n = 1).
Tabela 3882b. Ângulos de Bragg a várias tensões de feixe para o típico espaçamento d.
| Tensão acelerada (kV) | Comprimento de onda (nm) | Cristais | d-espaçamento (nm) | Bragg angle (° & mrad) |
| 100 | 0.0037 | Cristais biológicos típicos | 10 | 0,0106° (0,19 mrad) |
| 200 | Níquel (Ni) | 0,203 | 0.353° (6,16 mrad) |
Em experiências reais, diferentes da dispersão difusa, os picos de Bragg provêm da estrutura ordenada a longo prazo. As amostras cristalinas têm de ser inclinadas num goniómetro em TEM para:
i) Observar franjas e estruturas cristalinas.
ii) Determinar a orientação do cristal.
iii) Observar o contraste de difracção dos defeitos da malha com certos reflexos de Bragg ou orientação conhecida.
iv) Determinar o vector de defeitos da malha de Burgers.
Tabela 3882c. Scripts digitais de micrografia para calcular os ângulos de reflexão dos cristais.
| Estrutura de cristal | Scripts |
| FCC | Difracção de electrões, XRD |
| BCC | Difracção de electrões, XRD |
0 comentários