Por vezes, há mais do que uma forma de resolver um problema. Precisamos de aprender a comparar os diferentes algoritmos de desempenho e escolher o melhor para resolver um problema em particular. Ao analisarmos um algoritmo, consideramos sobretudo a complexidade temporal e espacial. A complexidade temporal de um algoritmo quantifica a quantidade de tempo que um algoritmo leva a executar em função da duração da entrada. Da mesma forma, a complexidade espacial de um algoritmo quantifica a quantidade de espaço ou memória tomada por um algoritmo para correr em função do comprimento da entrada.
A complexidade temporal e espacial depende de muitas coisas como hardware, sistema operativo, processadores, etc. Contudo, não consideramos nenhum destes factores durante a análise do algoritmo. Consideraremos apenas o tempo de execução de um algoritmo.
Vamos começar com um exemplo simples. Suponha que lhe é dado um array $A$ e um inteiro $$x$$ e tem de encontrar se $$x$ existe no array $A$$.
A solução simples para este problema é atravessar todo o array $A$$ e verificar se o elemento é igual a $x$.
for i : 1 to length of A if A is equal to x return TRUEreturn FALSECada operação no computador demora aproximadamente um tempo constante. Que cada operação demore $$c$ tempo. O número de linhas de código executadas depende efectivamente do valor de $$x$$. Durante a análise do algoritmo, na maior parte dos casos consideraremos o pior cenário, ou seja, quando $$x$ não está presente na matriz $$A$$. No pior caso, a condição será de $$N$ vezes em que $$N$ é o comprimento da matriz $$A$$. Assim, no pior caso, o tempo total de execução será $(N * c + c)$$. $N * c$$ para a condição se e $c$$ para a declaração de retorno ( ignorando algumas operações como a atribuição de $i$ ).
Como podemos ver, o tempo total depende da duração do array $A$$. Se a duração da matriz aumentar, o tempo de execução também aumentará.
Ordem de crescimento é como o tempo de execução depende da duração da entrada. No exemplo acima, podemos ver claramente que o tempo de execução é linearmente dependente do comprimento do array. A ordem de crescimento irá ajudar-nos a calcular o tempo de execução com facilidade. Ignoraremos os termos de ordem inferior, uma vez que os termos de ordem inferior são relativamente insignificantes para grandes entradas. Utilizamos notação diferente para descrever o comportamento limitador de uma função.
$O$notação:
Para denotar o limite superior assimptótico, utilizamos a notação $O$$. Para uma dada função $g(n)$, denota-se por $O(g(n))$ (pronuncia-se “big-oh de g de n”) o conjunto de funções:
$$O(g(n)) =$$ { $f(n)$ : existem constantes positivas $c$$ e $n_0$ tal que $0 \le f (n) \le c * g(n)$ para todos os $n \ge n_0$$
$$mega$$notação:
Para denotar o limite inferior assimptótico, utilizamos $$mega$notação. Para uma dada função $g(n)$, denotamos por $$\Omega(g(n))$ (pronuncia-se “big-omega de g de n”) o conjunto de funções:
$$\Omega(g(n)) =$$ { $f(n)$ : existem constantes positivas $c$$ e $n_0$ tal que $0 {g(n) }le c * g(n) {le f(n)$ para todos os $n {ge n_0$$}
$$$notação:
Para denotar o limite apertado assimptótico, usamos $$notação. Para uma dada função $g(n)$, denota-se por $$Theta(g(n))$ (pronuncia-se “big-theta de g de n”) o conjunto de funções:
$$Theta(g(n)) =$$ { $f (n)$ : existem constantes positivas $c_1,{$c_1,};c_2$$ e $n_0$$ tal que $0 {\i1}le c_1 * g(n) {\i}le c_2 * g(n)$ para todos os $n {\i}}g n_0$$ }
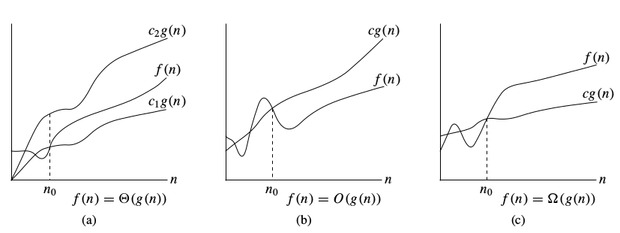
Notações de complexidade temporal
enquanto se analisa um algoritmo, consideramos sobretudo $O$notação porque nos dará um limite superior do tempo de execução i.e. o tempo de execução no pior dos casos.
Para calcular $O$-notação ignoraremos os termos de ordem inferior, uma vez que os termos de ordem inferior são relativamente insignificantes para grandes entradas.
Deixe $f(N) = 2 * N^2 + 3 * N + 5$
$O(f(N)) = O(2 * N^2 + 3 * N + 5) = O(N^2)$
Vamos considerar algum exemplo:
int count = 0;for (int i = 0; i < N; i++) for (int j = 0; j < i; j++) count++;Vejamos quantas vezes contamos+++ irão correr.
Quando $i = 0$$, correrá $0$ vezes.
Quando $i = 1$$, correrá $1$ vezes.
Quando $i = 2$$, correrá $2$ vezes e assim por diante.
Número total de vezes que contar++ correrá é $0 + 1 + 2 + … + (N-1) = \frac{N * (N-1)}{2}$$. Portanto, a complexidade temporal será $O(N^2)$.
int count = 0;for (int i = N; i > 0; i /= 2) for (int j = 0; j < i; j++) count++;Este é um caso complicado. No primeiro olhar, parece que a complexidade é $O(N * logN)$$. $N$ para o loop $j’s$ e $logN$$ para o loop $i’s$$, mas está errado. Vamos ver porquê.
P>Pense quantas vezes contará++ correrá.
Quando $i = N$$, correrá $N$ vezes.
Quando $i = N / 2$$, correrá $N / 2$$ vezes.
Quando $i = N / 4$$, correrá $N / 4$ vezes.
Número total de vezes contagem++ correrá $N + N / 2 + N / 4 + … + 1 = 2 * N$. Assim, a complexidade de tempo será $O(N)$.
A tabela abaixo destina-se a ajudá-lo a compreender o crescimento de várias complexidades de tempo comuns, e assim ajudá-lo a julgar se o seu algoritmo é suficientemente rápido para obter uma Aceitação ( assumindo que o algoritmo está correcto ).
| Length of Input (N) | Pior Aceite Algoritmo |
|---|---|
| $\le $ | $O(N!), O(N^6)$ |
| $\le $ | $O(2^N * N^2)$ |
| $\le $ | $O(2^N * N)$ |
| $\le 100$ | $O(N^4)$ |
| $\le 400$ | $O(N^3)$ |
| $\le 2K$ | $O(N^2 * logN)$ |
| $\le 10K$ | $O(N^2)$ |
| $\le 1M$ | $O(N * logN)$ |
| $\le 100M$ | $O(N), O(logN), O(1)$ |
Vai para o próximo tutorial
0 comentários