Em estatística, o intervalo é a dispersão dos seus dados do valor mais baixo para o valor mais alto na distribuição. É uma medida de variabilidade comummente utilizada.
Durante as medidas de tendência central, as medidas de variabilidade dão-lhe estatísticas descritivas para resumir o seu conjunto de dados.
A gama é calculada subtraindo o valor mais baixo do valor mais alto. Enquanto uma gama grande significa variabilidade alta, uma gama pequena significa variabilidade baixa numa distribuição.
Tabela de conteúdos
Calcular a gama
A fórmula para calcular a gama é:
p>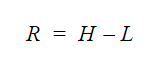
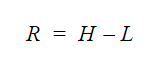
- R = intervalo
- H = valor mais alto
- L = valor mais baixo
O intervalo é a medida de variabilidade mais fácil de calcular. Para encontrar a gama, seguir estes passos:
- Ordenar todos os valores no seu conjunto de dados de baixo para alto.
- Subtrair o valor mais baixo do valor mais alto.
Este processo é o mesmo independentemente dos seus valores serem positivos ou negativos, ou números inteiros ou fracções.
| Participante | 3 | 4 | 5 | 6 | 7 | ||
|---|---|---|---|---|---|---|---|
| 37 | 19 | 31 | 29 | 21 | 26 | 33 | 36 |
First, ordenar os valores de baixo para alto para identificar o valor mais baixo (L) e o valor mais alto (H).
| Age | 19 | 21 | 26 | 29 | 31 | 33 | 36 | 37 |
|---|
Então subtrair o valor mais baixo do valor mais alto.
R = H – L
R = 37 – 19 = 18
O intervalo do nosso conjunto de dados é de 18 anos.
Qual a utilidade da gama?
A gama dá geralmente um bom indicador de variabilidade quando se tem uma distribuição sem valores extremos. Quando emparelhada com medidas de tendência central, a gama pode dizer-lhe sobre a amplitude da distribuição.
Mas a gama pode ser enganadora quando tem valores aberrantes no seu conjunto de dados. Um valor extremo nos dados dar-lhe-á um intervalo completamente diferente.
| Age | 19 | 21 | 26 | 29 | 31 | 33 | 36 | 61 |
|---|
Utilizando o mesmo cálculo, obtemos um resultado muito diferente desta vez:
R = H – L
R = 61 – 19 = 42
Com um outlier, a nossa gama é agora de 42 anos.
No exemplo acima, o intervalo indica muito mais variabilidade nos dados do que realmente existe. Embora tenhamos um grande intervalo, a maioria dos valores estão na realidade agrupados em torno de um meio claro.
Porque apenas dois números são utilizados, o intervalo é facilmente influenciado por valores aberrantes. Não lhe pode dizer sobre a forma da distribuição dos valores por si só.
Para ter uma ideia clara da variabilidade dos seus dados, a gama é melhor utilizada em combinação com outras medidas de variabilidade como a gama interquartil e o desvio padrão.
Perguntas frequentes sobre o intervalo
Nas estatísticas, o intervalo é a dispersão dos seus dados do valor mais baixo para o valor mais alto na distribuição. É a medida mais simples de variabilidade.
Não. Porque a fórmula da gama subtrai o número mais baixo do número mais alto, a gama é sempre zero ou um número positivo.
A variabilidade é medida mais frequentemente com as seguintes estatísticas descritivas:
- Gama: a diferença entre os valores mais altos e mais baixos
- Gama interquartil: o intervalo da metade média de uma distribuição
- desvio padrão: distância média da média
- variação: média das distâncias ao quadrado da média
Enquanto a tendência central lhe diz onde se encontra a maioria dos seus pontos de dados, a variabilidade resume a distância entre os seus pontos.
Os conjuntos de dados podem ter a mesma tendência central mas diferentes níveis de variabilidade ou vice-versa. Juntos, dão-lhe uma imagem completa dos seus dados.

0 comentários