|
Por definição, o declive ou inclinação de uma linha descreve o seu declive, inclinação, ou grau.
onde
m – inclinação
θ – ângulo de inclinação |
 |

Se os 2 Pontos forem Conhecidos
Se 1 Ponto e a Inclinação forem Conhecidos
p>Inclinação, por vezes referido como gradiente em matemática, é um número que mede a inclinação e direcção de uma linha, ou uma secção de uma linha que liga dois pontos, e é normalmente denotado por m. Geralmente, a inclinação de uma linha é medida pelo valor absoluto da sua inclinação, m. Quanto maior for o valor, mais inclinada é a linha. Dado m, é possível determinar a direcção da linha que m descreve, com base no seu sinal e valor:
- Uma linha está a aumentar, e sobe da esquerda para a direita quando m > 0
- Uma linha está a diminuir, e desce da esquerda para a direita quando m < 0
- Uma linha tem uma inclinação constante, e é horizontal quando m = 0
- Uma linha vertical tem uma inclinação indefinida, uma vez que resultaria numa fracção com 0 como denominador. Consultar a equação fornecida abaixo.
Inclinação é essencialmente mudança de altura sobre mudança de distância horizontal, e é frequentemente referida como “subida sobre corrida”. Tem aplicações em inclinações geográficas, bem como em engenharia civil, como a construção de estradas. No caso de uma estrada, a “subida” é a mudança de altitude, enquanto a “corrida” é a diferença de distância entre dois pontos fixos, desde que a distância para a medição não seja suficientemente grande para que a curvatura da terra deva ser considerada como um factor. A inclinação é representada matematicamente como:
| m = | >br>
x2 – x1 >br> |
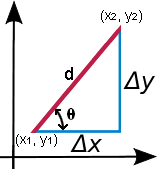
Na equação acima, y2 – y1 = Δy, ou mudança vertical, enquanto x2 – x1 = Δx, ou mudança horizontal, como se mostra no gráfico fornecido. Também se pode ver que Δx e Δy são segmentos de linha que formam um triângulo direito com hipotenusa d, sendo d a distância entre os pontos (x1, y1) e (x2, y2). Uma vez que Δx e Δy formam um triângulo direito, é possível calcular d utilizando o teorema de Pitágoras. Consulte a Calculadora do Triângulo para mais detalhes sobre o teorema de Pitágoras, bem como sobre como calcular o ângulo de inclinação θ fornecido na calculadora acima. Resumidamente:
d = √(x2 – x1)2 + (y2 – y1)2
A equação acima é o teorema de Pitágoras na sua raiz, onde a hipotenusa d já foi resolvida, e os outros dois lados do triângulo são determinados subtraindo os dois valores x e y dados por dois pontos. Dados dois pontos, é possível encontrar θ usando a seguinte equação:
m = tan(θ)
Dados os pontos (3,4) e (6,8) encontrar a inclinação da linha, a distância entre os dois pontos, e o ângulo de inclinação:
| m = | = |
d = √(6 – 3)2 + (8 -) 4)2 = 5
| >br>>>br>> |
| θ = tan-1( | >br>>>br>> | ) = 53.13° |
Enquanto isto ultrapassa o âmbito desta calculadora, para além do seu uso linear básico, o conceito de inclinação é importante no cálculo diferencial. Para funções não lineares, a taxa de variação de uma curva varia, e a derivada de uma função num dado ponto é a taxa de variação da função, representada pela inclinação da linha tangente à curva nesse ponto.
0 comentários