Cálculo – Cálculo de valores mínimos e máximos Parte I

Calculus – Determinação
Mínimo & Valores máximos
parte I

>p>>br>>p>>p> Um dos usos mais importantes do cálculo é a determinação de valores mínimos e máximos. Isto tem as suas aplicações no fabrico, finanças, engenharia, e uma série de outras indústrias. Antes de examinarmos um exemplo do mundo real, devemos aprender como calcular tais valores.

P>Vamos utilizar para o nosso primeiro exemplo, a equação 2X2 -5X -7 = 0

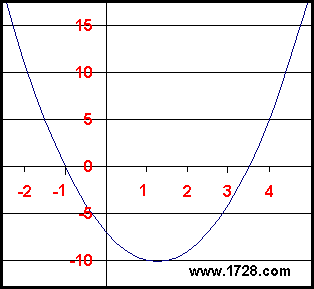
Esta é uma equação quadrática numa variável. Ou seja, é uma equação da forma:ax2 + bx + c = 0
Com equações deste tipo, sabemos que quando o termo “a” é positivo, o gráfico da curva será “côncavo para cima” (em forma de U) e portanto a equação terá um valor mínimo mas nenhum valor máximo (ok – tecnicamente, o valor máximo é infinito). Olhando para o gráfico, vemos que o ponto mínimo é aproximadamente X = 1,5 e Y = -10. Haverá uma forma de determinar o ponto mínimo sem fazer um gráfico da equação e obter um valor exacto? Sim, há !

Localize o gráfico. Se os valores da inclinação fossem calculados para pontos do lado esquerdo da curva, poderia ver-se que a inclinação seria sempre negativa, mas torna-se “menos negativa” quanto mais próxima a curva se aproxima do mínimo (o fundo). Se a inclinação fosse calculada ao longo do lado direito da curva, o valor seria sempre positivo e os valores da inclinação aumentariam quanto mais longe do “fundo” os pontos estivessem.

Então, é lógico pensar que a inclinação é zero nesse ponto do “fundo” e portanto a derivada também é zero nesse ponto.
Então, tomemos a derivada de 2X2 -5X -7 = 0 que é:

4X – 5 Quando 4X -5 é igual a zero, X =1,25 o que significa que, neste ponto, existe um valor mínimo. Quanto ao valor ‘Y’, vamos para a equação original e introduzimos o valor de X como 1,25. Y = 2X2 -5X -7Y = 2*(1.25)2 -5*1.25 -7Y = -10.125 Então, no ponto X=1,25, Y= -10,125 existe um valor mínimo.

Neste exemplo sabíamos que estávamos a obter um valor mínimo porque o agarrámos. Além disso, declarámos que a “regra” para equações quadráticas é tal que quando o termo “a” é positivo, a curva será “côncava”. Existe ainda um terceiro método para determinar se um ponto é um valor máximo ou mínimo.
Se tomarmos a segunda derivada e se esse valor for positivo, então estamos a lidar com um valor mínimo.
Neste exemplo, tomando a derivada da derivada temos o valor 4 que é positivo e por isso sabemos que é um mínimo.

Para equações do tipo aX2 + bX + c =0, uma ferramenta útil a utilizar é a Calculadora de Equações Quadráticas. Não só calcula as raízes da equação, como também mostra a derivada e o ponto em que o máximo ou mínimo existe.

O segundo exemplo que vamos analisar é muito semelhante ao anterior, excepto que é “côncavo para baixo” em vez de “côncavo para cima”. Se pensa que compreende os conceitos apresentados até agora, então passe à Parte II

Okay, vamos examinar esta equação:

-4X2 + 4X + 13 = 0Desde que esta é uma equação quadrática numa variável com o termo “a” sendo negativo, sabemos que o gráfico da curva terá a forma de “côncava para baixo” (com a forma de ∩) e terá um valor máximo mas nenhum valor mínimo (está bem, se quiser ser técnico, o seu valor mínimo é o infinito negativo. Está satisfeito agora?).
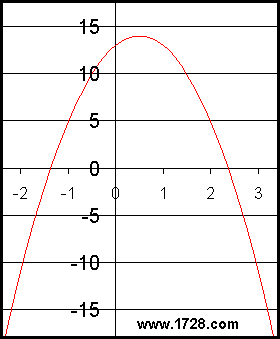
Aprendemos com o primeiro exemplo que a forma de calcular um ponto máximo (ou mínimo) é encontrar o ponto em que a derivada de uma equação é igual a zero: