O que são Estiramentos Horizontais e Encolhimentos?
Estiramentos e encolhimentos horizontais, respectivamente, puxar horizontalmente o gráfico de base, ou empurrá-lo em conjunto, deixando o conceito y inalterado para ancorar o gráfico.
p>Definição
Para a função de base f (x) e uma constante k, onde k > 0 e k ≠ 1, a função dada por
g(x) = f (kx),
pode ser esboçado encolhendo horizontalmente f (x) por um factor de 1/k se k > 1
ou
por estiramento horizontal f (x) por um factor de 1/k
se 0 < k < 1.
p>uma extensão horizontal ou contracção por um factor de 1/k significa que o ponto (x, y) no gráfico de f(x) é transformado ao ponto (x/k, y) no gráfico de g(x).
Exemplos de Alongamentos e Encolhimentos Horizontais
Considerar as seguintes funções base,
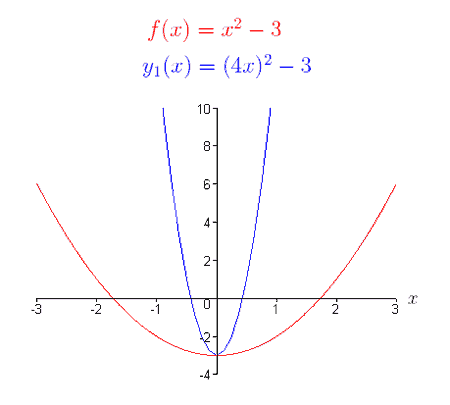
(1) f (x) = x2 – 3,
(2) g(x) = cos (x).
A representação gráfica da função (1), f (x), é uma parábola. O que supõe que o gráfico de
y1(x) = f (4x)
não se parece? Usando a definição de f (x), podemos escrever y1(x) como,
y1(x) = f (4x) = (4x)2 – 3 = 16×2-3.
b>Baseado na definição de encolhimento horizontal, o gráfico de y1(x) deve parecer-se com o gráfico de
f (x), encolhido horizontalmente por um factor de 1/4. Veja os gráficos de f (x) e y1(x).
Função (2), g (x), é uma função co-seno. Como seria o gráfico de
y2(x) = g(2/3x)
parece? Usando os nossos conhecimentos sobre estiramentos horizontais, o gráfico de y2(x) deve parecer-se com o gráfico de base g(x) esticado horizontalmente por um factor de 3/2. Para verificar isto, podemos escrever y2(x) como,
y2(x) = g(2/3x) = cos (2/3x),
construir uma tabela de valores, e traçar o gráfico da nova função. Como se pode ver, o gráfico de y2(x) é de facto o gráfico de base g(x) esticado horizontalmente por um factor de 3/2.

0 comentários