As belezas ocultas em Pi(π)

>/div>>>>figcaption>Qualquer rotação é uma expressão de π.

A razão lógica parece críptica; é porque pi é uma bela fonte para gerar números aleatórios. Contudo, a verdadeira razão parece ser para que os países possam mostrar a sua tecnologia a outros países, porque o cálculo de triliões de dígitos de pi necessita de um computador muito potente. Por exemplo, no episódio do Star Trek ” Wolf in the Fold”, Spock manda o computador malvado “computar para o último dígito o valor de Pi”. Assim, pedir a um computador para computar Pi é chamado “um teste de stress”, e pode fazê-lo falhar.

Por outro lado, nós, humanos, somos criadores incómodos. Ficar em casa e beber chá é uma bela actividade, mas quando nos aborrecemos tentamos escalar o mais alto das montanhas, antes de encontrarmos um tigre ou eu tentar memorizar os dígitos de pi como Chao Lu, que memorizou correctamente os primeiros 67,890 dígitos de pi. Vamos continuar a fazer estas coisas porque gostamos de compreender o mundo que nos rodeia.

Em 12 de Setembro de 1962, John F. Kennedy fez um discurso sobre o programa espacial. Ele disse:

“Ainda não há conflitos, nenhum preconceito, nenhum conflito nacional no espaço exterior. Os seus perigos são hostis para todos nós. A sua conquista merece o melhor de toda a humanidade, e a sua oportunidade de cooperação pacífica muitos nunca mais voltam. Mas porquê, dizem alguns, a lua? Porquê escolher isto como nosso objectivo? E podem muito bem perguntar porquê escalar a montanha mais alta? Nós escolhemos ir à lua. Escolhemos ir à Lua nesta década e fazemos as outras coisas, não porque sejam fáceis, mas porque são difíceis, porque esse objectivo servirá para organizar e medir o melhor das nossas energias e competências, porque esse desafio é um desafio que estamos dispostos a aceitar, um que não estamos dispostos a adiar, e um que pretendemos vencer, e os outros também.

Estamos inevitavelmente ligados ao passado, e pi é um fio que percorreu toda a história humana. É por isso que podemos dizer que enquanto houver pessoas, haverá sempre alguém que apenas se pergunta o que se segue. E asseguro-vos que algures no mundo há um matemático ou cientista que usa pi para algo importante para o nosso universo porque pi ainda é a misteriosa constante da natureza.

A afirmação anterior é totalmente verdadeira porque sempre houve alguém que trabalha em pi. A matemática é tão antiga como a civilização. Pi tem sido estudada pela raça humana há quase 4000 anos. Quando os últimos mamutes estavam a extinguir-se, as pessoas estudavam Pi. Tanto quanto sabemos, Arquimedes da Grécia antiga foi um dos primeiros humanos que calculou Pi. Ele ajudou muito provavelmente os fabricantes de rodas. Mas como estimou ele o valor de pi?

P>Primeiro, ele viu que todos os polígonos eram um círculo. Segundo Arquimedes, se continuarmos a aumentar o número dos lados de um polígono, aproximar-nos-íamos do círculo perfeito. Por outras palavras, um pentágono é mais círculo do que um quadrado, mas um hexágono é mais círculo do que um pentágono, e assim por diante… Assim, o lendário matemático Arquimedes definiu um círculo como um polígono regular com um número extremamente grande de lados há mais de dois mil anos.

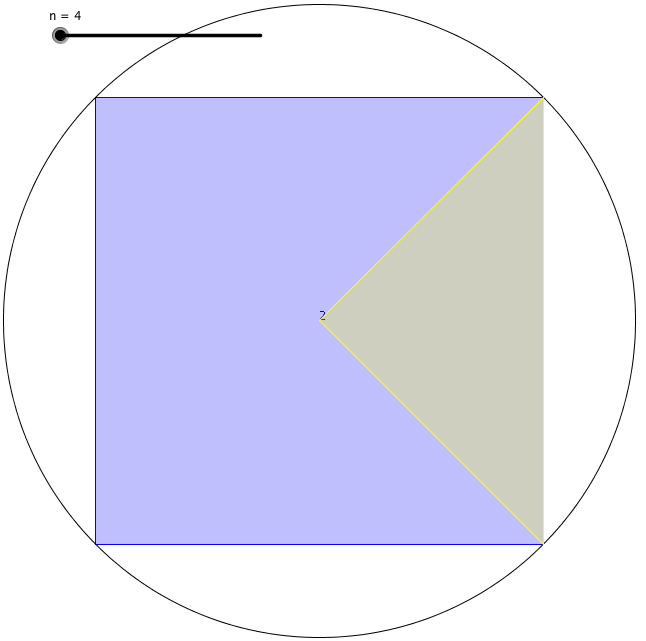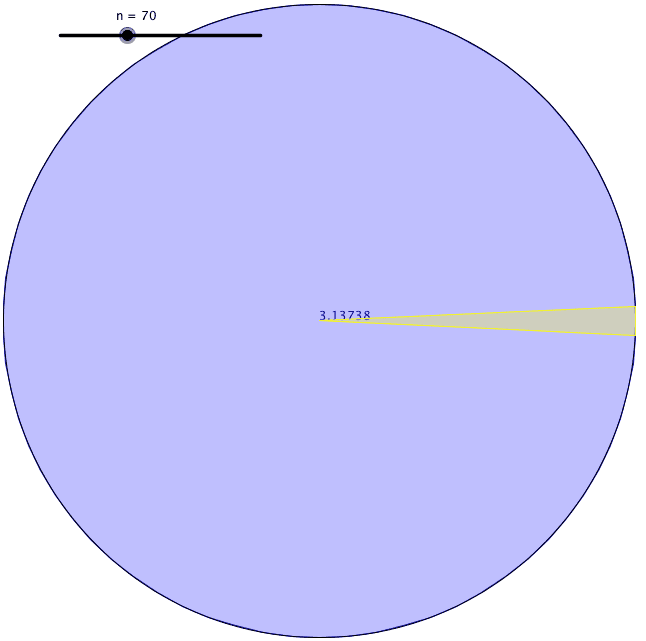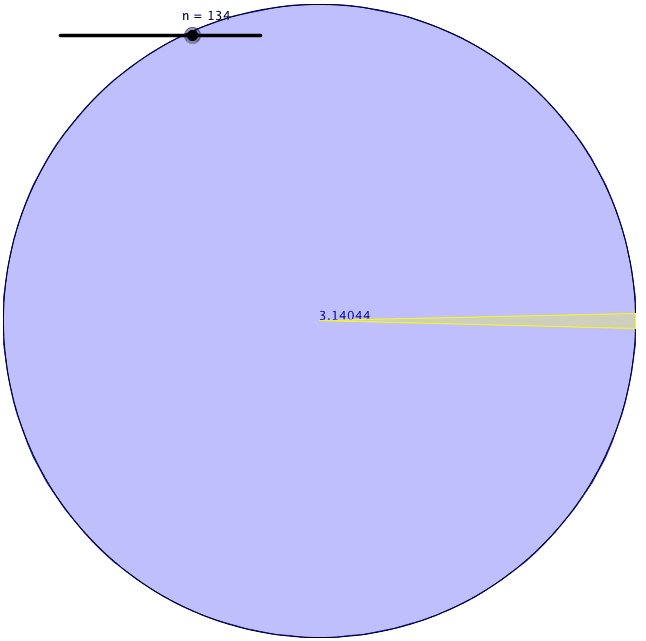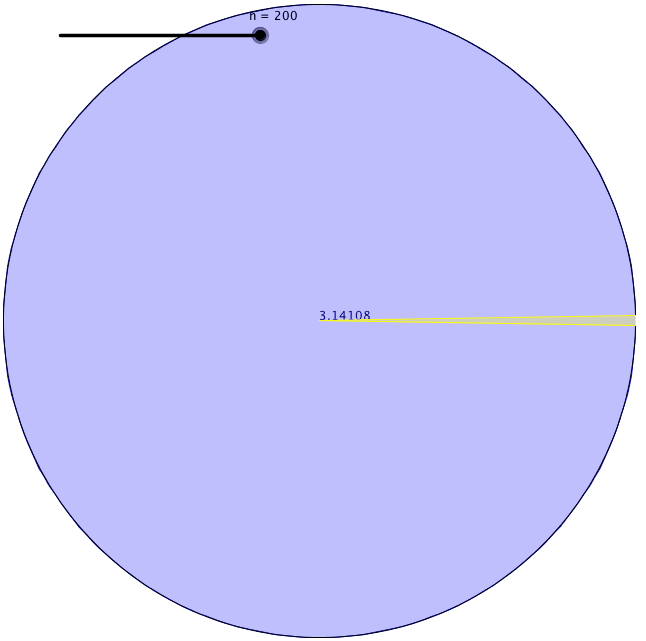
A sua definição é útil porque medir uma superfície curva era difícil de fazer com precisão. Encontrou uma forma de encontrar a circunferência de um círculo. Primeiro, desenhou um quadrado com os seus cantos tocando o perímetro de um círculo e encontrou o perímetro do quadrado inscrito. Em segundo lugar, desenhou outro quadrado com os seus lados tocando também o perímetro do círculo e encontrou o perímetro do quadrado circunscrito. Chegou à conclusão de que a circunferência do círculo tinha de estar algures entre o valor desses dois perímetros de quadrados.

Utilizando este método, contudo, a diferença entre esses dois valores era bastante grande quando ele utilizava quadrados. Assim, desenhou pentagões para ver os limites superior e inferior da circunferência do círculo. Nessa altura, obteve uma gama mais pequena de limites. Depois disso, continuou a aumentar o número de faces do polígono que estava a desenhar dentro e fora do círculo. Cada vez que o fazia, a sua estimativa estava a tornar-se mais precisa. Arquimedes subiu para um polígono regular de 96 lados até se esgotar. Os limites inferior e superior que ele encontrou foram 3.1408 e 3.1429. Assim, calculou π com duas casas decimais.

Arquimedes necessitava de melhorias porque o tempo de vida de hsi não ia ser suficientemente longo para encontrar os outros dígitos de pi à mão. Os matemáticos precisavam de descobrir fórmulas mais eficientes e novas técnicas.

Antes de o poderem fazer, precisavam de descobrir Álgebra. No início, as pessoas estavam a usar sinais para os dígitos. Por exemplo, digamos que você e o seu vizinho têm 75 cavalos juntos e têm 35 cavalos. É preciso encontrar o número de cavalos que o seu vizinho tem. Sem álgebra, a solução demorará muito tempo. Mas após a descoberta da álgebra, apenas utilizamos equações para resolver os problemas. Neste exemplo específico, podemos escrever 75 = x + 35 onde x são os cavalos do seu vizinho. Escrever tal equação e utilizar uma variável em vez de um número foi revolucionário para o mundo clássico. A álgebra permitiu cálculos muito mais fáceis em toda a matemática.

A adopção da álgebra por grandes matemáticos inspirou toda uma nova forma de ver o mundo. O próximo grande salto no cálculo pi foi a invenção do cálculo. Depois disso, os matemáticos começaram a trabalhar em séries infinitas. Uma série infinita é uma expressão com números adicionados um após o outro até ao infinito, e por vezes estas séries infinitas convergem para um valor particular.

Existem agora muitos métodos disponíveis para calcular Pi. Gottfried Leibniz encontrou pi no infinito. James Gregory encontrou a equação abaixo para pi. Ele estava a trabalhar numa das espantosas séries infinitas para a função tangente inversa abaixo. Ele adicionou infinitamente muitos números pequenos juntos e encontrou pi.

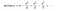
P>Ele colocou x = 1 no inverso…série tangente. Mostrou-nos quanto mais avançamos, mais perto da estimativa de pi nos aproximamos. No entanto, para obter 10 dígitos de pi, precisamos de escrever cerca de 5 mil milhões de fracções para adicionar.