A Lei de Hess

Porquê funciona

Uma visão pictórica da Lei de Hess como aplicada ao calor da equação é ilustrativa. Na figura 1, os reagentes C(s) + 2 H2O(g) são colocados juntos numa caixa, representando o estado dos materiais envolvidos na reacção anterior à reacção. Os produtos CO2(g) + 2 H2(g) são colocados juntos numa segunda caixa, que representa o estado dos materiais envolvidos após a reacção. A seta de reacção que liga estas caixas é rotulada com o calor desta reacção. Agora pegamos nestes mesmos materiais e colocamo-los numa terceira caixa contendo C(s), O2(g), e 2 H2(g). Esta caixa é ligada às caixas do reagente e do produto com setas de reacção, rotuladas pelos aquecedores de reacção em equação e equação .

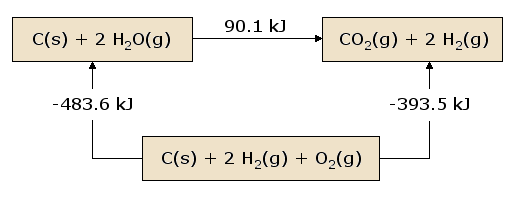
Esta imagem da Lei de Hess revela que o calor de reacção ao longo do “caminho” que liga directamente o estado do reagente ao estado do produto é exactamente igual ao calor total de reacção ao longo do “caminho” alternativo que liga os reagentes aos produtos através do estado intermédio que contém {(C_{(s)}, { O_{2(g)}, e 2 { H_{2(g)}). Uma consequência da nossa observação da Lei de Hess é, portanto, que o calor líquido evoluiu ou absorvido durante uma reacção é independente do caminho que liga o reagente ao produto (esta afirmação está novamente sujeita à nossa restrição de que todas as reacções no caminho alternativo devem ocorrer em condições de pressão constante).

Uma visão ligeiramente diferente dos resultados da figura 1 desde o início na caixa do reagente e seguindo um circuito completo através das outras caixas que conduzem de volta à caixa do reagente, somando os aquecedores líquidos de reacção à medida que avançamos. Descobrimos que o calor líquido transferido (mais uma vez desde que todas as reacções ocorram sob pressão constante) é exactamente zero. Esta é uma afirmação da conservação de energia: a energia no estado reactivo não depende dos processos que produziram esse estado. Portanto, não podemos extrair qualquer energia dos reagentes através de um processo que simplesmente recria os reagentes. Se tal não fosse o caso, poderíamos produzir infinitamente quantidades ilimitadas de energia seguindo o caminho sinuoso que reproduz continuamente os reactantes iniciais.

Por este raciocínio, podemos definir uma função energética cujo valor para os reactantes é independente da forma como o estado do reactante foi preparado. Do mesmo modo, o valor desta função energética no estado do produto é independente da forma como os produtos são preparados. Escolhemos esta função, H, para que a alteração da função, ΔH = Hproducts – Hreactants, seja igual ao calor de reacção q em condições de pressão constante. H, a que chamamos entalpia, é uma função de estado, uma vez que o seu valor depende apenas do estado dos materiais em consideração, ou seja, da temperatura, pressão e composição destes materiais.

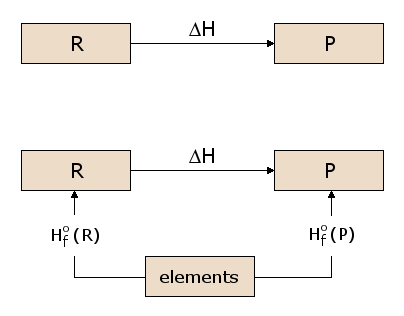
O conceito de uma função de estado é algo análogo à ideia de elevação. Considere a diferença de elevação entre o primeiro andar e o terceiro andar de um edifício. Esta diferença é independente do caminho que escolhemos para ir do primeiro andar para o terceiro andar. Podemos simplesmente subir dois lances de escadas, ou podemos subir um lance de escadas, percorrer o comprimento do edifício, depois percorrer um segundo lance de escadas. Ou podemos andar de elevador. Podemos até andar lá fora e ter uma grua a elevar-nos até ao telhado do edifício, de onde descemos para o terceiro andar. Cada caminho produz exactamente o mesmo ganho de elevação, ainda que a distância percorrida seja significativamente diferente de um caminho para o outro. Isto é simplesmente porque a elevação é uma “função de estado”. A nossa elevação, de pé no terceiro andar, é independente de como chegámos ao terceiro andar, e o mesmo se aplica ao primeiro andar. Uma vez que a elevação é assim uma função de estado, o ganho da elevação é independente do caminho. Agora, a existência de uma função de estado de energia H é de considerável importância no cálculo dos aquecedores de reacção. Consideremos a reacção prototípica na subfigura 2.1, com os reagentes R a serem convertidos em produtos P. Queremos calcular o calor absorvido ou libertado nesta reacção, que é ΔH. Uma vez que H é uma função de estado, podemos seguir qualquer caminho de R a P e calcular ΔH ao longo desse caminho. Na subfigura 2.2, consideramos um desses caminhos possíveis, que consiste em duas reacções que passam por um estado intermédio contendo todos os átomos envolvidos na reacção, cada um na forma elementar. Este é um estado intermédio útil, uma vez que pode ser utilizado para qualquer reacção química possível. Por exemplo, na figura 1, os átomos envolvidos na reacção são C, H, e O, cada um dos quais representado no estado intermédio na forma elementar. Podemos ver na subfigura 2.2 que o ΔH para a reacção global é agora a diferença entre o ΔH na formação dos produtos P a partir dos elementos e o ΔH na formação dos reagentes R a partir dos elementos.

Os valores ΔH para a formação de cada material a partir dos elementos são assim de utilidade geral no cálculo de ΔH para qualquer reacção de interesse. Assim, definimos a reacção de formação padrão para o reagente R, como

elementos em estado padrão R

e o calor envolvido nesta reacção é a entalpia padrão de formação, designada por ΔHf°. O subscrito f, que significa “formação”, indica que o ΔH é para a reacção de criação do material a partir dos elementos em estado padrão. O sobrescrito ° indica que as reacções ocorrem sob condições de pressão padrão constante de 1 atm. A partir da subfiguração 2.2, vemos que o calor de qualquer reacção pode ser calculado a partir de

\

Tabelas extensas de valores ΔH°f (Tabela T1) foram compiladas que nos permitem calcular com total confiança o calor de reacção para qualquer reacção de interesse, mesmo incluindo reacções hipotéticas que podem ser difíceis de realizar ou impossivelmente lentas de reagir.