Parce qu’il y a tant de faits fascinants sur pi, c’est aussi le nombre le plus étudié de l’histoire des mathématiques jusqu’à présent. De nombreuses personnes veulent mémoriser les chiffres de pi, et non les chiffres d’autres nombres irrationnels (YouTube, PBS NewsHour). Il pousse les gens à la folie et au chaos. Les mathématiciens s’efforcent de calculer exactement pi depuis des siècles.
Donc, faut-il arrêter de travailler sur pi ou continuer à chercher une meilleure approximation ? Est-ce que supposer que pi est égal à 3,14 est suffisant ? Ou est-il suffisant d’utiliser 40 chiffres de pi pour trouver la circonférence de la Voie lactée avec une erreur inférieure à la taille d’un proton (JPL NASA) ? Les 152 premiers chiffres sont-ils suffisants pour trouver la circonférence de l’univers observable à 93 milliards d’années-lumière (WIRED) ? Des centaines de mathématiciens essaient depuis des années de trouver d’autres chiffres de pi. C’est comme essayer d’aller sur la lune, puis sur la planète suivante, et ainsi de suite… Mais pourquoi ? Pourquoi les mathématiciens se donnent-ils la peine de calculer d’autres chiffres ? Pourquoi les 34,1 trillions de chiffres de pi ne sont-ils pas suffisants ? Est-ce parce que pi se cache dans chaque cercle ?
La raison logique semble cryptique, c’est que pi est une belle source pour générer des nombres aléatoires. Cependant, la vraie raison semble être pour que les pays puissent montrer leur technologie aux autres pays, car le calcul des trillions de chiffres de pi nécessite un ordinateur très puissant. Par exemple, dans l’épisode de Star Trek « Wolf in the Fold », Spock déjoue l’ordinateur maléfique en lui ordonnant de « calculer jusqu’au dernier chiffre la valeur de Pi ». Ainsi, demander à un ordinateur de calculer Pi s’appelle » un test de stress « , et peut le faire planter.
D’autre part, nous, les humains, sommes des créateurs maladroits. Rester à la maison et boire du thé est une belle activité, mais lorsque nous nous ennuyons, nous essayons d’escalader les plus hautes montagnes, d’affronter un tigre ou de mémoriser les chiffres de pi comme Chao Lu, qui a mémorisé correctement les 67 890 premiers chiffres de pi. Nous continuerons à faire ces choses parce que nous aimons comprendre le monde qui nous entoure.
Le 12 septembre 1962, John F. Kennedy a prononcé un discours sur le programme spatial. Il a déclaré :
« Il n’y a pas encore de querelle, pas de préjugé, pas de conflit national dans l’espace. Ses dangers sont hostiles pour nous tous. Sa conquête mérite le meilleur de toute l’humanité, et l’occasion d’une coopération pacifique ne se représentera peut-être jamais. Mais pourquoi, disent certains, la lune ? Pourquoi l’avoir choisie comme objectif ? Et ils pourraient bien demander pourquoi escalader la plus haute montagne ? Nous avons choisi d’aller sur la lune. Nous choisissons d’aller sur la lune au cours de cette décennie et de faire les autres choses, non pas parce qu’elles sont faciles, mais parce qu’elles sont difficiles, parce que cet objectif servira à organiser et à mesurer le meilleur de nos énergies et de nos compétences, parce que ce défi est un défi que nous sommes prêts à accepter, un défi que nous ne voulons pas reporter, et un défi que nous avons l’intention de gagner, et les autres aussi.
Nous sommes inévitablement liés au passé, et le pi est un fil conducteur de toute l’histoire humaine. C’est pourquoi on peut dire que tant qu’il y aura des gens, il y aura toujours quelqu’un qui se demandera ce que sera la suite. Et je vous assure que quelque part dans le monde, il y a un mathématicien ou un scientifique qui utilise pi pour quelque chose d’important pour notre univers parce que pi est toujours la constante mystérieuse de la nature.
L’affirmation précédente est tout à fait vraie parce qu’il y a toujours eu quelqu’un qui travaille sur Pi. Les mathématiques sont aussi vieilles que la civilisation. Pi a été étudié par la race humaine depuis près de 4000 ans. Lorsque les derniers mammouths s’éteignaient, les gens étudiaient Pi. Pour autant que nous le sachions, Archimède, de la Grèce antique, est l’un des premiers humains à avoir calculé Pi, probablement pour aider les fabricants de roues. Mais comment a-t-il estimé la valeur de pi ?
D’abord, il a vu que tous les polygones comme un cercle. Selon Archimède, si vous continuez à augmenter le nombre de côtés d’un polygone, vous vous rapprocherez du cercle parfait. En d’autres termes, un pentagone est plus cercle qu’un carré, mais un hexagone est plus cercle qu’un pentagone, et ainsi de suite… Ainsi, le légendaire mathématicien Archimède a défini un cercle comme un polygone régulier avec un nombre extrêmement élevé de côtés, il y a plus de deux mille ans.
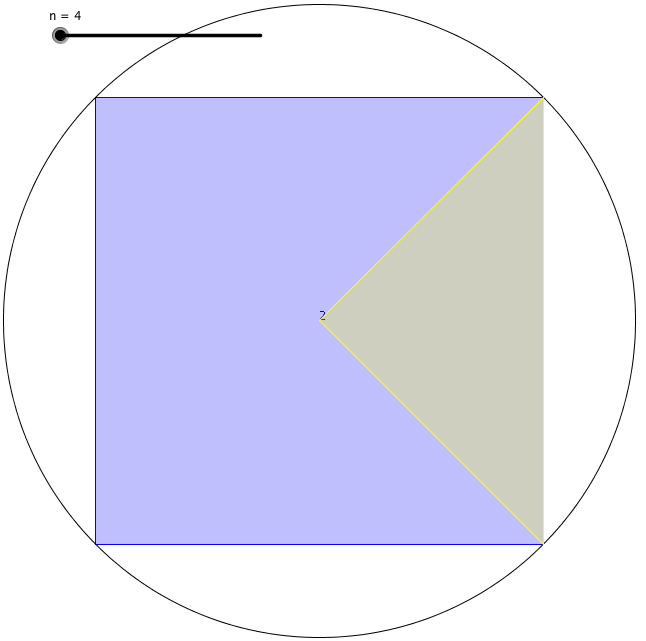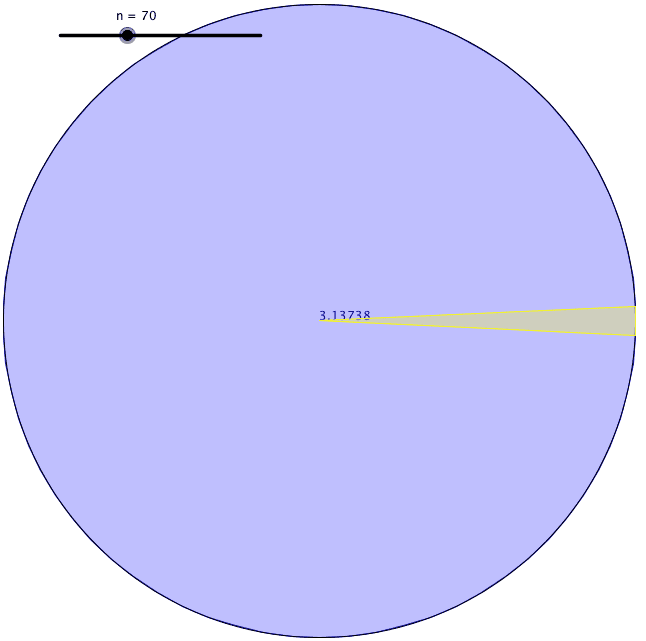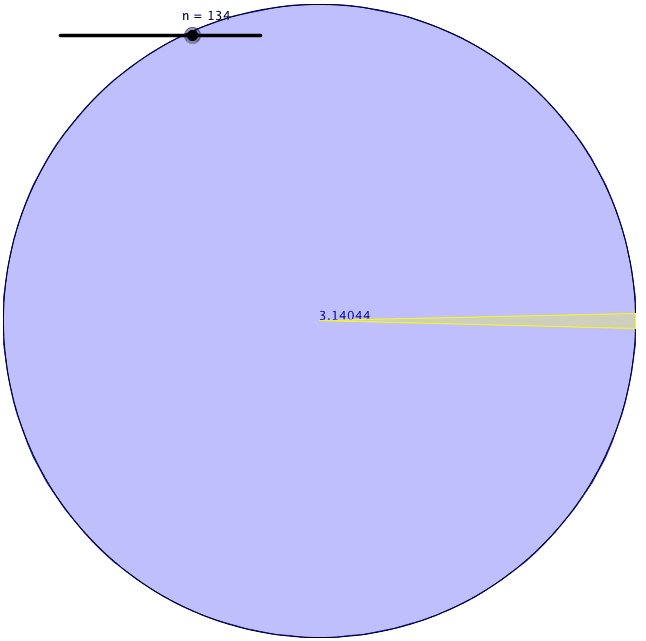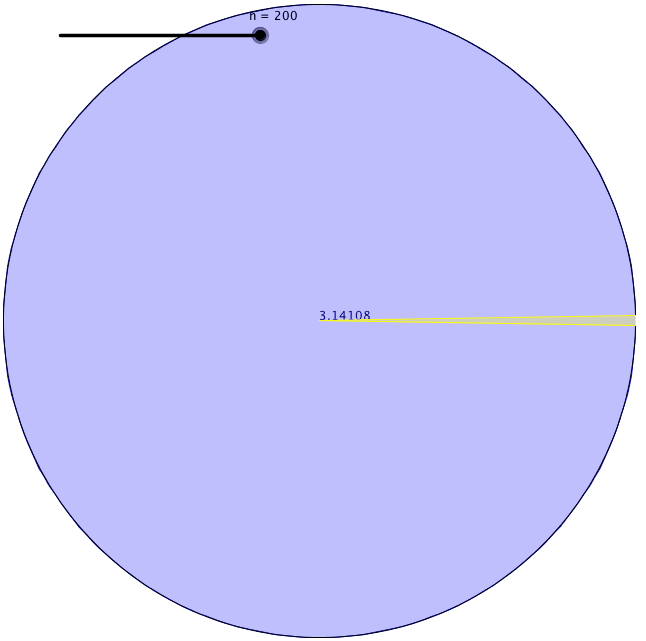
Sa définition est utile car mesurer une surface courbe était difficile à faire avec précision. Il a trouvé un moyen de trouver la circonférence d’un cercle. Tout d’abord, il a dessiné un carré dont les coins touchent le périmètre d’un cercle et a trouvé le périmètre du carré inscrit. Ensuite, il a dessiné un autre carré dont les côtés touchent également le périmètre du cercle et a trouvé le périmètre du carré circonscrit. Il est arrivé à la conclusion que la circonférence du cercle devait se trouver quelque part entre la valeur de ces deux périmètres de carrés.
En utilisant cette méthode, cependant, la différence entre ces deux valeurs était assez grande lorsqu’il utilisait des carrés. Il a donc dessiné des pentagones pour voir les limites supérieure et inférieure de la circonférence du cercle. Il a obtenu une plus petite gamme de limites à ce moment-là. Ensuite, il a continué à augmenter le nombre de faces du polygone qu’il dessinait à l’intérieur et à l’extérieur du cercle. À chaque fois qu’il faisait cela, son estimation devenait plus précise. Archimède est arrivé à un polygone régulier de 96 côtés jusqu’à ce qu’il soit épuisé. Les limites inférieure et supérieure qu’il a trouvées cette fois étaient 3,1408 et 3,1429. Ainsi, il a calculé π avec deux décimales.
La méthode d’Archimède devait être améliorée car sa durée de vie n’allait pas être assez longue pour trouver les autres chiffres de pi à la main. Les mathématiciens devaient découvrir des formules plus efficaces et de nouvelles techniques.
Avant de pouvoir le faire, ils devaient découvrir l’algèbre. Au début, les gens utilisaient des signes pour les chiffres. Par exemple, disons que vous et votre voisin avez 75 chevaux ensemble et que vous avez 35 chevaux. Vous devez trouver le nombre de chevaux de votre voisin. Sans l’algèbre, la solution prendra beaucoup de temps. Mais après la découverte de l’algèbre, nous utilisons simplement des équations pour résoudre les problèmes. Dans cet exemple précis, nous pouvons écrire 75 = x + 35 où x est le nombre de chevaux de votre voisin. Écrire une telle équation et utiliser une variable au lieu d’un nombre était révolutionnaire pour le monde classique. L’algèbre a permis des calculs beaucoup plus faciles dans l’ensemble des mathématiques.
L’adoption de l’algèbre par les grands mathématiciens a inspiré une toute nouvelle façon de voir le monde. Le prochain grand saut dans le calcul de pi a été l’invention du calcul. Après cela, les mathématiciens ont commencé à travailler sur les séries infinies. Une série infinie est une expression avec des nombres ajoutés les uns après les autres jusqu’à l’infini, et parfois ces séries infinies convergent vers une valeur particulière.
Il existe aujourd’hui de nombreuses méthodes pour calculer Pi. Gottfried Leibniz a trouvé pi à l’infini. James Gregory a trouvé l’équation ci-dessous pour pi. Il travaillait sur l’une des étonnantes séries infinies pour la fonction tangente inverse ci-dessous. Il a ajouté une infinité de petits nombres ensemble et a trouvé pi.
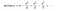
Il a mis x = 1 dans la série inverse-tangente. Il nous a montré que plus on va loin, plus on se rapproche de l’estimation de pi. Cependant, pour obtenir 10 chiffres de pi, nous devons écrire environ 5 milliards de fractions à additionner.
0 commentaire