Une procédure pas à pas pour utiliser le test F
Pour atteindre les objectifs ci-dessus, nous allons suivre les étapes suivantes :
- Formuler la statistique du test F alias la statistique F.
- Identifier la fonction de densité de probabilité de la variable aléatoire que la statistique F représente en supposant que l’hypothèse nulle est vraie.
- Placer les valeurs dans la formule de la statistique F et calculer la valeur de probabilité correspondante en utilisant la fonction de densité de probabilité trouvée à l’étape 2. Il s’agit de la probabilité d’observer la valeur de la statistique F en supposant que l’hypothèse nulle est vraie.
- Si la probabilité trouvée à l’étape 3 est inférieure au seuil d’erreur tel que 0,05, rejeter l’hypothèse nulle et accepter l’hypothèse alternative à un niveau de confiance de (1,0 – seuil d’erreur), par exemple 1-0,05 = 0,95 (c’est-à-dire un niveau de confiance de 95 %). Sinon, acceptez l’hypothèse nulle avec une probabilité d’erreur égale au seuil d’erreur, par exemple à 0,05 ou 5 %.
Plongeons-nous dans ces étapes.
Étape 1 : Développer l’intuition pour la statistique de test
Rappelons que le test F mesure combien un modèle complexe est meilleur par rapport à une version plus simple du même modèle dans sa capacité à expliquer la variance de la variable dépendante.
Envisageons deux modèles de régression 1 et 2 :
- Let Modèle 1 a k_1 paramètres. Le modèle 2 a k_2 paramètres.
- Let k_1 < k_2
- Donc, le modèle 1 est la version plus simple du modèle 2, c’est-à-dire que le modèle 1 est le modèle restreint et le modèle 2 est le modèle non restreint. Le modèle 1 peut être imbriqué dans le modèle 2.
- Laissez RSS_1 et RSS_2 être la somme des carrés des erreurs résiduelles après l’ajustement du modèle 1 et du modèle 2 au même ensemble de données.
- Laissez n être le nombre d’échantillons de données.
Avec les définitions ci-dessus, la statistique du test F de régression peut être exprimée sous forme de ratio comme suit :

La formule de la statistique F vous permet de calculer la part de la variance de la variable dépendante, le modèle plus simple n’est pas en mesure d’expliquer par rapport au modèle complexe, exprimé en tant que fraction de la variance inexpliquée du modèle complexe.
Dans l’analyse de régression, l’erreur quadratique moyenne du modèle ajusté est une excellente mesure de la variance inexpliquée. Ce qui explique les termes RSS du numérateur et du dénominateur.
Le numérateur et le dénominateur sont convenablement échelonnés en utilisant les degrés de liberté disponibles correspondants.
La statistique F est elle-même une variable aléatoire.
Déterminons à quelle fonction de densité de probabilité obéit la statistique F.
Etape 2 : identification de la fonction de densité de probabilité de la statistique F
Notez que le numérateur et le dénominateur de la statistique de test contiennent tous deux des sommes de carrés d’erreurs résiduelles. Rappelez-vous également qu’en régression, une erreur résiduelle se trouve être une variable aléatoire avec une certaine fonction de densité de probabilité (ou de masse de probabilité), c’est-à-dire une PDF ou une PMF selon qu’elle est continue ou discrète. Dans ce cas, nous sommes concernés par la recherche de la PDF de la statistique F.
Si nous supposons que les erreurs résiduelles des deux modèles sont 1) indépendantes et 2) normalement distribuées, ce qui se trouve être incidemment des exigences de la régression par moindres carrés ordinaires, alors on peut voir que le numérateur et le dénominateur de la formule de la statistique F contiennent des sommes de carrés de variables aléatoires indépendantes et normalement distribuées.
On peut prouver que la somme des carrés de k variables aléatoires indépendantes et normales suit la PDF de la distribution du Khi-deux(k).

On peut donc montrer que le numérateur et le dénominateur de la formule de la statistique F obéissent chacun à des versions mises à l’échelle de deux distributions du Khi-deux.
Avec un peu de mathématiques, on peut également montrer que le rapport de deux variables aléatoires distribuées par le chi-deux convenablement mises à l’échelle est lui-même une variable aléatoire qui suit la distribution F, dont la PDF est présentée ci-dessous.

En d’autres termes :
Si la variable aléatoire X a la PDF de la distribution F avec les paramètres d_1 et d_2, c’est-à-dire . :
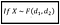
.
alors , On peut montrer que X s’exprime comme le rapport de deux variables aléatoires X_1 et X_2, dont chacune a la densité de probabilité d’une distribution du khi-carré. c’est-à-dire :

Rappellez-vous maintenant que k_1 et k_2 sont le nombre de variables dans les modèles simple et complexe M1 et M2 introduits précédemment, et que n est le nombre d’échantillons de données.
Substituez d_1 et d_2 comme suit :
d_1 = (k_2 – k_1) qui est la différence des degrés de liberté des résidus des deux modèles M1 et M2 à comparer, et
d_2 = (n – k_2) qui est le degré de liberté des résidus du modèle complexe M2,
Avec ces substitutions, nous pouvons réécrire la formule de la distribution F comme suit :

Comparons la formule ci-dessus avec la formule de la statistique F (reproduite ci-dessous), où nous savons que le numérateur et le dénominateur contiennent des PDF de distributions du Khi-deux convenablement mises à l’échelle :

En comparant ces deux formules, il est clair que :
- Le degré de liberté ‘a’ de la distribution du Khi-deux au numérateur est (k1 – k2).
- Le degré de liberté ‘b’ de la distribution du Khi-deux au dénominateur est (n – k2).
- La statistique du test F a la même PDF que celle de la distribution F.
En d’autres termes, la statistique F suit la distribution F.
Étape 3 : Calcul de la valeur de la statistique F
Si vous utilisez l’estimateur MCO de statsmodels, cette étape est une opération en une ligne. Il vous suffit d’imprimer OLSResults.summary() et vous obtiendrez :
- La valeur de la statistique F et,
- La valeur ‘p’ correspondante, c’est-à-dire la probabilité de rencontrer cette valeur, à partir du PDF de la distribution F.
La bibliothèque statsmodels fera le travail fastidieux des deux calculs.
print(ols_results.summary())
Ceci imprime ce qui suit :

ETAPE 4 : Déterminer si l’hypothèse nulle peut être acceptée
Puisque OLSResults.summary() imprime la probabilité d’occurrence de la statistique F dans l’hypothèse où l’hypothèse nulle est vraie, il nous suffit de comparer cette probabilité à notre valeur alpha seuil. Dans notre exemple, la valeur p renvoyée par .summary() est de 4,84E-16, ce qui est un nombre extrêmement faible. Bien plus petite que même alpha = 0,01. Ainsi, il y a beaucoup moins de 1% de chances que la statistique F de 136,7 ait pu se produire par hasard dans l’hypothèse d’une hypothèse Nulle valide.
Nous rejetons donc l’hypothèse Nulle et acceptons l’hypothèse alternative H_1 selon laquelle le modèle complexe, c’est-à-dire le modèle à variables décalées, malgré ses défauts évidents, est capable d’expliquer la variance de la variable dépendante Cours de clôture mieux que le modèle à ordonnée à l’origine seulement.
0 commentaire