La loi de Hess

Pourquoi ça marche

Une vue imagée de la loi de Hess appliquée à la chaleur d’équation est illustrative. Dans la figure 1, les réactifs C(s) + 2 H2O(g) sont placés ensemble dans une boîte, représentant l’état des matériaux impliqués dans la réaction avant la réaction. Les produits CO2(g) + 2 H2(g) sont placés ensemble dans une deuxième boîte représentant l’état des matériaux impliqués après la réaction. La flèche de réaction reliant ces boîtes est étiquetée avec la chaleur de cette réaction. Maintenant, nous prenons ces mêmes matériaux et les plaçons dans une troisième boîte contenant C(s), O2(g) et 2 H2(g). Cette boîte est reliée aux boîtes du réactif et du produit par des flèches de réaction, étiquetées par les chaleurs de réaction dans l’équation et l’équation .

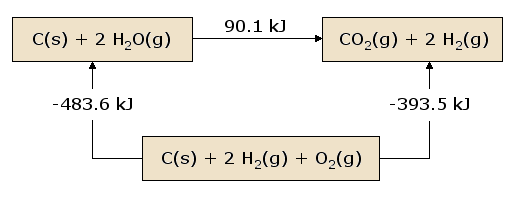
Cette image de la loi de Hess révèle que la chaleur de réaction le long du  » chemin  » reliant directement l’état réactif à l’état produit est exactement égale à la chaleur totale de réaction le long du  » chemin  » alternatif reliant les réactifs aux produits via l’état intermédiaire contenant \(C_{(s)}\), \(O_{2(g)}\), et 2 \(H_{2(g)}\). Une conséquence de notre observation de la loi de Hess est donc que la chaleur nette dégagée ou absorbée au cours d’une réaction est indépendante du chemin reliant le réactif au produit (cette affirmation est à nouveau soumise à notre restriction selon laquelle toutes les réactions dans le chemin alternatif doivent se produire dans des conditions de pression constante).

Une vue légèrement différente de la figure 1 résulte du fait de commencer à la boîte du réactif et de suivre un circuit complet à travers les autres boîtes menant à la boîte du réactif, en additionnant les chaleurs nettes de réaction au fur et à mesure. Nous découvrons que la chaleur nette transférée (à condition que toutes les réactions se produisent sous une pression constante) est exactement nulle. Il s’agit d’une affirmation de la conservation de l’énergie : l’énergie de l’état réactif ne dépend pas des processus qui ont produit cet état. Par conséquent, nous ne pouvons extraire aucune énergie des réactifs par un processus qui recrée simplement les réactifs. Si ce n’était pas le cas, nous pourrions produire sans fin des quantités illimitées d’énergie en suivant le chemin détourné qui reproduit continuellement les réactifs initiaux.

Par ce raisonnement, nous pouvons définir une fonction d’énergie dont la valeur pour les réactifs est indépendante de la façon dont l’état réactif a été préparé. De même, la valeur de cette fonction énergétique à l’état produit est indépendante de la façon dont les produits sont préparés. Nous choisissons cette fonction, H, de sorte que la variation de la fonction, ΔH = Hproduits – Hréactifs, soit égale à la chaleur de réaction q dans des conditions de pression constante. H, que nous appelons l’enthalpie, est une fonction d’état, puisque sa valeur ne dépend que de l’état des matériaux considérés, c’est-à-dire de la température, de la pression et de la composition de ces matériaux.

Le concept de fonction d’état est quelque peu analogue à l’idée d’élévation. Considérons la différence d’élévation entre le premier étage et le troisième étage d’un bâtiment. Cette différence est indépendante du chemin que nous choisissons pour aller du premier étage au troisième étage. Nous pouvons simplement monter deux volées d’escaliers, ou nous pouvons monter une volée d’escaliers, marcher le long du bâtiment, puis monter une deuxième volée d’escaliers. Nous pouvons aussi prendre l’ascenseur. Nous pouvons même sortir et demander à une grue de nous hisser sur le toit du bâtiment, d’où nous descendrons au troisième étage. Chaque chemin produit exactement le même dénivelé, même si la distance parcourue est sensiblement différente d’un chemin à l’autre. Cela s’explique simplement par le fait que l’élévation est une « fonction d’état ». Notre élévation, lorsque nous nous trouvons au troisième étage, est indépendante de la façon dont nous sommes arrivés au troisième étage, et il en va de même pour le premier étage. Puisque l’élévation est donc une fonction d’état, le gain d’élévation est indépendant du chemin. Maintenant, l’existence d’une fonction d’état énergétique H est d’une importance considérable pour le calcul des chaleurs de réaction. Considérons la réaction prototypique de la sous-figure 2.1, avec des réactifs R transformés en produits P. Nous souhaitons calculer la chaleur absorbée ou libérée dans cette réaction, qui est ΔH. Comme H est une fonction d’état, nous pouvons suivre n’importe quel chemin de R à P et calculer ΔH le long de ce chemin. Dans la sous-figure 2.2, nous considérons un de ces chemins possibles, consistant en deux réactions passant par un état intermédiaire contenant tous les atomes impliqués dans la réaction, chacun sous forme élémentaire. Cet état intermédiaire est utile car il peut être utilisé pour n’importe quelle réaction chimique possible. Par exemple, dans la figure 1, les atomes impliqués dans la réaction sont C, H et O, chacun d’entre eux étant représenté dans l’état intermédiaire sous forme élémentaire. Nous pouvons voir dans la sous-figure 2.2 que le ΔH pour la réaction globale est maintenant la différence entre le ΔH dans la formation des produits P à partir des éléments et le ΔH dans la formation des réactifs R à partir des éléments.

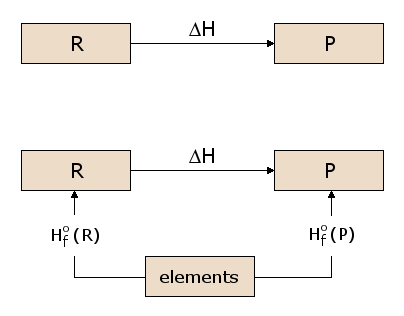
Les valeurs de ΔH pour la formation de chaque matériau à partir des éléments sont donc d’une utilité générale pour calculer le ΔH de toute réaction d’intérêt. On définit donc la réaction de formation standard du réactif R, comme

éléments à l’état standard R

et la chaleur impliquée dans cette réaction est l’enthalpie standard de formation, désignée par ΔHf°. L’indice f, qui signifie  » formation « , indique que le ΔH concerne la réaction créant la matière à partir des éléments à l’état standard. L’exposant ° indique que les réactions se produisent dans des conditions de pression standard constante de 1 atm. D’après la sous-figure 2.2, nous voyons que la chaleur de n’importe quelle réaction peut être calculée à partir de

Des tableaux étendus de valeurs de ΔH°f (tableau T1) ont été compilés, ce qui nous permet de calculer en toute confiance la chaleur de réaction pour n’importe quelle réaction d’intérêt, même en incluant des réactions hypothétiques qui peuvent être difficiles à réaliser ou impossibles à faire réagir lentement.

.