KDnuggets

Quoique vous vous situiez sur la question du sex-appeal de la science des données, il est tout simplement impossible d’ignorer l’importance continue des données, et notre capacité à les analyser, les organiser et les contextualiser. En s’appuyant sur ses vastes réserves de données sur l’emploi et sur les commentaires des employés, Glassdoor a classé le scientifique des données au premier rang de sa liste des 25 meilleurs emplois en Amérique. Le rôle est donc là pour rester, mais il est indéniable que les spécificités du travail du scientifique spécialisé dans les données vont évoluer. Avec des technologies comme l’apprentissage automatique qui deviennent de plus en plus courantes, et des domaines émergents comme l’apprentissage profond qui gagnent une traction significative parmi les chercheurs et les ingénieurs – et les entreprises qui les embauchent – les scientifiques des données continuent de surfer sur la crête d’une incroyable vague d’innovation et de progrès technologique.

Bien qu’il soit important d’avoir une forte capacité de codage, la science des données ne se résume pas à l’ingénierie logicielle (en fait, ayez une bonne familiarité avec Python et vous êtes prêt à partir). Les scientifiques des données vivent à l’intersection du codage, des statistiques et de la pensée critique. Comme le dit Josh Wills, « le data scientist est une personne qui est meilleure en statistiques que n’importe quel programmeur et meilleure en programmation que n’importe quel statisticien. » Je connais personnellement trop d’ingénieurs logiciels qui cherchent à se transformer en data scientist et qui utilisent aveuglément des frameworks d’apprentissage automatique tels que TensorFlow ou Apache Spark sur leurs données sans avoir une compréhension approfondie des théories statistiques qui les sous-tendent. C’est ainsi que vient l’étude de l’apprentissage statistique, un cadre théorique pour l’apprentissage automatique puisant dans les domaines de la statistique et de l’analyse fonctionnelle.

Pourquoi étudier l’apprentissage statistique ? Il est important de comprendre les idées derrière les différentes techniques, afin de savoir comment et quand les utiliser. Il faut d’abord comprendre les méthodes les plus simples, afin d’appréhender les plus sophistiquées. Il est important d’évaluer avec précision les performances d’une méthode, pour savoir si elle fonctionne bien ou mal. En outre, il s’agit d’un domaine de recherche passionnant, qui a des applications importantes dans les sciences, l’industrie et la finance. En fin de compte, l’apprentissage statistique est un ingrédient fondamental de la formation d’un data scientist moderne. Voici quelques exemples de problèmes d’apprentissage statistique :

• Identifier les facteurs de risque du cancer de la prostate.
• Classifier un phonème enregistré sur la base d’un log-périodogramme.
• Prédire si une personne aura une crise cardiaque sur la base de mesures démographiques, alimentaires et cliniques.
• Personnaliser un système de détection des spams par courrier électronique.
• Identifier les chiffres d’un code postal écrit à la main.
• Classer un échantillon de tissu dans l’une de plusieurs classes de cancer.
• Établir la relation entre le salaire et les variables démographiques dans les données d’enquête sur la population.

Dans mon dernier semestre à l’université, j’ai fait une étude indépendante sur l’exploration de données. La classe couvre des matériaux expansifs provenant de 3 livres : Intro to Statistical Learning (Hastie, Tibshirani, Witten, James), Doing Bayesian Data Analysis(Kruschke), et Time Series Analysis and Applications (Shumway, Stoffer). Nous avons fait beaucoup d’exercices sur l’analyse bayésienne, la chaîne de Markov Monte Carlo, la modélisation hiérarchique, l’apprentissage supervisé et non supervisé. Cette expérience a renforcé mon intérêt pour le domaine académique du Data Mining et m’a convaincu de me spécialiser davantage dans ce domaine. Récemment, j’ai suivi le cours en ligne Statistical Learning sur Stanford Lagunita, qui couvre tout le matériel du livre Intro to Statistical Learning que j’ai lu dans mon étude indépendante. Maintenant, étant exposé deux fois au contenu, je veux partager les 10 techniques statistiques du livre que, selon moi, tout data scientist devrait apprendre pour être plus efficace dans la gestion des grands ensembles de données.

Avant de passer à ces 10 techniques, je veux faire la différence entre l’apprentissage statistique et l’apprentissage automatique. J’ai déjà écrit l’un des billets Medium les plus populaires sur l’apprentissage automatique, alors je suis sûr d’avoir l’expertise nécessaire pour justifier ces différences :

• L’apprentissage automatique est né comme un sous-domaine de l’intelligence artificielle.
• L’apprentissage statistique est né comme un sous-domaine de la statistique.
• L’apprentissage automatique met davantage l’accent sur les applications à grande échelle et la précision des prédictions.
• L’apprentissage statistique met l’accent sur les modèles et leur interprétabilité, ainsi que sur la précision et l’incertitude.
• Mais la distinction est devenue et plus floue, et il y a beaucoup de « fertilisation croisée. »
• L’apprentissage machine a la main en marketing !

1 – Régression linéaire :

En statistique, la régression linéaire est une méthode pour prédire une variable cible en ajustant la meilleure relation linéaire entre la variable dépendante et la variable indépendante. Le meilleur ajustement se fait en s’assurant que la somme de toutes les distances entre la forme et les observations réelles en chaque point est la plus petite possible. L’ajustement de la forme est « optimal » dans le sens où aucune autre position ne produirait moins d’erreur étant donné le choix de la forme. Les deux principaux types de régression linéaire sont la régression linéaire simple et la régression linéaire multiple. La régression linéaire simple utilise une seule variable indépendante pour prédire une variable dépendante en ajustant une relation linéaire optimale. La régression linéaire multiple utilise plus d’une variable indépendante pour prédire une variable dépendante en ajustant une meilleure relation linéaire.

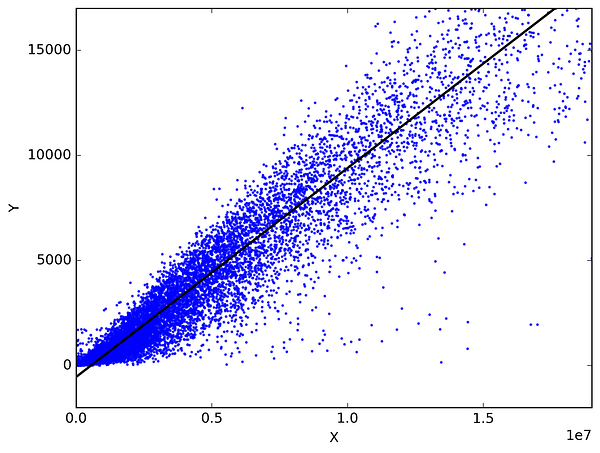
Prenez 2 choses quelconques que vous utilisez dans votre vie quotidienne et qui sont liées. Par exemple, j’ai les données de mes dépenses mensuelles, de mon revenu mensuel et du nombre de voyages par mois pour les 3 dernières années. Maintenant, je dois répondre aux questions suivantes :

• Quelles seront mes dépenses mensuelles pour l’année prochaine ?
• Quel facteur (revenu mensuel ou nombre de voyages par mois) est le plus important pour décider de mes dépenses mensuelles ?
• Comment le revenu mensuel et les voyages par mois sont corrélés aux dépenses mensuelles ?

2 – Classification:

La classification est une technique d’exploration de données qui attribue des catégories à une collection de données afin de favoriser des prédictions et des analyses plus précises. Parfois aussi appelée arbre de décision, la classification est l’une des nombreuses méthodes destinées à rendre efficace l’analyse de très grands ensembles de données. Deux grandes techniques de classification se distinguent : La régression logistique et l’analyse discriminante.

La régression logistique est l’analyse de régression appropriée à mener lorsque la variable dépendante est dichotomique (binaire). Comme toutes les analyses de régression, la régression logistique est une analyse prédictive. La régression logistique est utilisée pour décrire des données et expliquer la relation entre une variable binaire dépendante et une ou plusieurs variables indépendantes de niveau nominal, ordinal, intervalle ou ratio. Types de questions qu’une régression logistique peut examiner :

• Comment la probabilité d’avoir un cancer du poumon (Oui vs Non) change-t-elle pour chaque livre supplémentaire de surpoids et pour chaque paquet de cigarettes fumé par jour ?
• Est-ce que le poids corporel l’apport calorique, l’apport en graisses et l’âge des participants ont une influence sur les crises cardiaques (Oui vs Non) ?

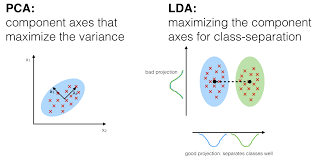
Dans l’analyse discriminante, 2 ou plusieurs groupes ou grappes ou populations sont connus a priori et 1 ou plusieurs nouvelles observations sont classées dans 1 des populations connues en fonction des caractéristiques mesurées. L’analyse discriminante modélise la distribution des prédicteurs X séparément dans chacune des classes de réponse, puis utilise le théorème de Bayes pour les retourner en estimations de la probabilité de la catégorie de réponse étant donné la valeur de X. De tels modèles peuvent être linéaires ou quadratiques.

• L’analyse discriminante linéaire calcule des « scores discriminants » pour chaque observation afin de classer dans quelle classe de variable de réponse elle se trouve. Ces scores sont obtenus en trouvant des combinaisons linéaires des variables indépendantes. Elle suppose que les observations de chaque classe sont tirées d’une distribution gaussienne multivariée et que la covariance des variables prédicteurs est commune à tous les k niveaux de la variable de réponse Y.
• L’analyse discriminante quadratique fournit une approche alternative. Comme LDA, QDA suppose que les observations de chaque classe de Y sont tirées d’une distribution gaussienne. Cependant, contrairement à la LDA, la QDA suppose que chaque classe possède sa propre matrice de covariance. En d’autres termes, on ne suppose pas que les variables prédicteurs ont une variance commune à chacun des k niveaux de Y.

3 – Méthodes de rééchantillonnage :

Le rééchantillonnage est la méthode qui consiste à tirer des échantillons répétés à partir des échantillons de données originaux. Il s’agit d’une méthode non paramétrique d’inférence statistique. En d’autres termes, la méthode de rééchantillonnage n’implique pas l’utilisation des tables de distribution génériques afin de calculer des valeurs de probabilité p approximatives.

Le rééchantillonnage génère une distribution d’échantillonnage unique sur la base des données réelles. Il utilise des méthodes expérimentales, plutôt que des méthodes analytiques, pour générer la distribution d’échantillonnage unique. Il donne des estimations non biaisées car il est basé sur les échantillons non biaisés de tous les résultats possibles des données étudiées par le chercheur. Afin de comprendre le concept de rééchantillonnage, vous devez comprendre les termes Bootstrapping et validation croisée :

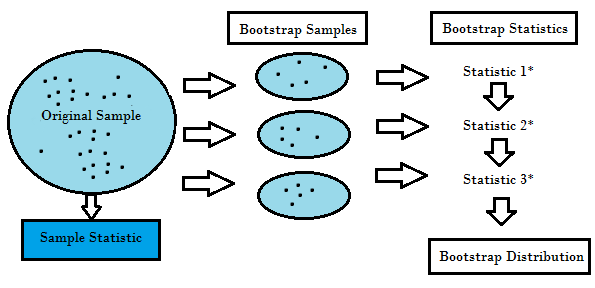
• Le Bootstrapping est une technique qui aide dans de nombreuses situations comme la validation des performances d’un modèle prédictif, les méthodes d’ensemble, l’estimation du biais et de la variance du modèle. Elle fonctionne en échantillonnant avec remplacement à partir des données originales, et en prenant les points de données « non choisis » comme cas de test. Nous pouvons faire cela plusieurs fois et calculer le score moyen comme estimation de la performance de notre modèle.
• D’autre part, la validation croisée est une technique pour valider la performance du modèle, et elle est faite en divisant les données de formation en k parties. Nous prenons les k – 1 parties comme notre ensemble de formation et utilisons la partie « retenue » comme notre ensemble de test. Nous répétons cela k fois différemment. Enfin, nous prenons la moyenne des k scores comme notre estimation de performance.

En général, pour les modèles linéaires, les moindres carrés ordinaires sont le principal critère à prendre en compte pour les adapter aux données. Les 3 méthodes suivantes sont les approches alternatives qui peuvent fournir une meilleure précision de prédiction et une meilleure interprétabilité du modèle pour l’ajustement des modèles linéaires.

4 – Sélection de sous-ensemble:

Cette approche identifie un sous-ensemble des p prédicteurs que nous pensons être liés à la réponse. Nous ajustons ensuite un modèle en utilisant les moindres carrés des caractéristiques du sous-ensemble.

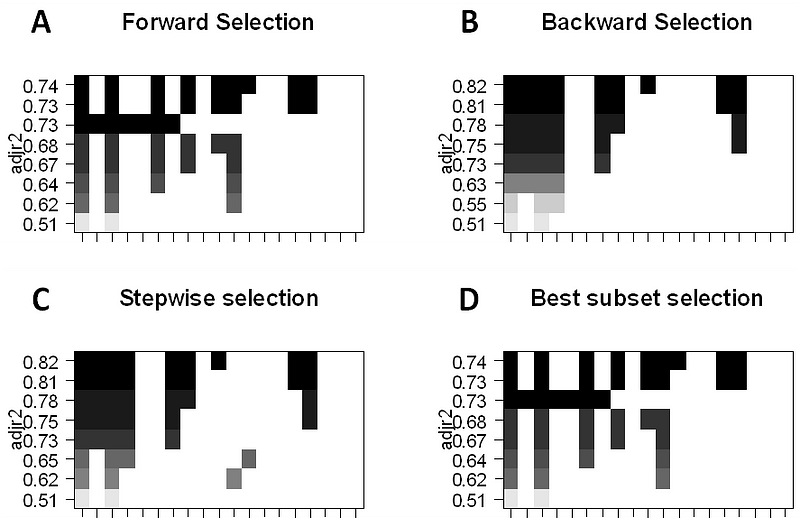
• Sélection du meilleur sous-ensemble : Ici, nous ajustons une régression MCO distincte pour chaque combinaison possible des p prédicteurs, puis nous examinons les ajustements du modèle résultant. L’algorithme est décomposé en 2 étapes : (1) Ajustement de tous les modèles qui contiennent k prédicteurs, où k est la longueur maximale des modèles, (2) Sélection d’un seul modèle en utilisant l’erreur de prédiction validée par croisement. Il est important d’utiliser l’erreur de test ou de validation, et non l’erreur de formation pour évaluer l’adéquation du modèle car le RSS et le R² augmentent de façon monotone avec un plus grand nombre de variables. La meilleure approche consiste à effectuer une validation croisée et à choisir le modèle présentant le R² le plus élevé et le RSS le plus faible sur les estimations d’erreur de test.
• La sélection pas à pas avant considère un sous-ensemble beaucoup plus petit de ppredicteurs. Elle commence par un modèle ne contenant aucun prédicteur, puis ajoute des prédicteurs au modèle, un par un jusqu’à ce que tous les prédicteurs soient dans le modèle. L’ordre des variables ajoutées est la variable, qui donne la plus grande amélioration d’addition à l’ajustement, jusqu’à ce que plus aucune variable n’améliore l’ajustement du modèle en utilisant l’erreur de prédiction validée croisée.
• La sélection pas à pas à rebours commence will tous les p prédicteurs dans le modèle, puis supprime itérativement le prédicteur le moins utile, un à la fois.
• Les méthodes hybrides suivent l’approche pas à pas avant, cependant, après avoir ajouté chaque nouvelle variable, la méthode peut également supprimer les variables qui ne contribuent pas à l’ajustement du modèle.

5 – Shrinkage:

Cette approche ajuste un modèle impliquant tous les p prédicteurs, cependant, les coefficients estimés sont rétrécis vers zéro par rapport aux estimations des moindres carrés. Ce rétrécissement, alias régularisation a pour effet de réduire la variance. Selon le type de rétrécissement effectué, certains des coefficients peuvent être estimés comme étant exactement nuls. Ainsi, cette méthode effectue également une sélection des variables. Les deux techniques les plus connues pour rétrécir les estimations des coefficients vers zéro sont la régression ridge et le lasso.

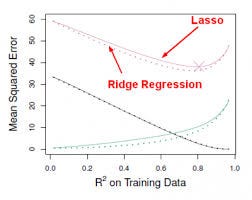
• La régression ridge est similaire aux moindres carrés, sauf que les coefficients sont estimés en minimisant une quantité légèrement différente. La régression ridge, comme les MCO, cherche des estimations de coefficients qui réduisent les RSS, cependant ils ont également une pénalité de rétrécissement lorsque les coefficients se rapprochent de zéro. Cette pénalité a pour effet de rétrécir les estimations des coefficients vers zéro. Sans entrer dans les détails mathématiques, il est utile de savoir que la régression ridge réduit les caractéristiques ayant la plus petite variance dans l’espace colonne. Comme dans l’analyse en composantes principales, la régression ridge projette les données dans un espace ddirectionnel, puis rétrécit les coefficients des composantes à faible variance plus que les composantes à forte variance, qui sont équivalentes aux composantes principales les plus grandes et les plus petites.
• La régression ridge a au moins un inconvénient ; elle inclut tous les p prédicteurs dans le modèle final. Le terme de pénalité fixera beaucoup d’entre eux près de zéro, mais jamais exactement à zéro. Ce n’est généralement pas un problème pour la précision de la prédiction, mais cela peut rendre le modèle plus difficile à interpréter les résultats. Lasso surmonte cet inconvénient et est capable de forcer certains des coefficients à zéro, à condition que s soit suffisamment petit. Étant donné que s = 1 donne lieu à une régression MCO normale, lorsque s s’approche de 0, les coefficients se réduisent à zéro. Ainsi, la régression Lasso effectue également une sélection de variables.