Dove si trova una funzione in un punto alto o basso? Il calcolo può aiutare!
Un massimo è un punto alto e un minimo è un punto basso:
In una funzione che cambia in modo uniforme un massimo o un minimo è sempre dove la funzione si appiattisce (tranne che per un punto di sella).
Dove si appiattisce? Dove la pendenza è zero.
Dove la pendenza è zero? Ce lo dice la derivata!
Tuffiamoci subito con un esempio:
Esempio: Una palla viene lanciata in aria. La sua altezza in qualsiasi momento t è data da:
h = 3 + 14t – 5t2
Qual è la sua altezza massima?
Utilizzando le derivate possiamo trovare la pendenza di questa funzione:
![]() h = 0 + 14 – 5(2t)
h = 0 + 14 – 5(2t)
= 14 – 10t
(Vedi sotto questo esempio per come abbiamo trovato la derivata.)
Ora trova quando la pendenza è zero:
La pendenza è zero a t = 1,4 secondi
E l’altezza in quel momento è:
E quindi:
L’altezza massima è 12.8 m (a t = 1,4 s)
Un rapido ripasso sulle derivate
Una derivata trova sostanzialmente la pendenza di una funzione.
Nell’esempio precedente abbiamo preso questo:
h = 3 + 14t – 5t2
e abbiamo ottenuto questa derivata:
![]() h = 0 + 14 – 5(2t)
h = 0 + 14 – 5(2t)
= 14 – 10t
Che ci dice la pendenza della funzione in qualsiasi momento t
Abbiamo usato queste regole di derivazione:
- La pendenza di un valore costante (come 3) è 0
- La pendenza di una linea come 2x è 2, quindi 14t ha una pendenza di 14
- Una funzione quadrata come t2 ha una pendenza di 2t, quindi 5t2 ha una pendenza di 5(2t)
- E poi li abbiamo sommati: 0 + 14 – 5(2t)
Come facciamo a sapere che è un massimo (o un minimo)?
Lo abbiamo visto sul grafico! Ma per il resto… le derivate vengono di nuovo in soccorso.
Prendiamo la derivata della pendenza (la derivata seconda della funzione originale):
La derivata di 14 – 10t è -10
Questo significa che la pendenza diventa sempre più piccola (-10): viaggiando da sinistra a destra la pendenza inizia positiva (la funzione sale), passa per lo zero (il punto piatto), e poi la pendenza diventa negativa (la funzione scende):

Una pendenza che diventa più piccola (e passa per 0) significa un massimo.
Questo si chiama Test della derivata seconda
Sul grafico sopra ho mostrato la pendenza prima e dopo, ma in pratica facciamo il test nel punto in cui la pendenza è zero:
Test della derivata seconda
Quando la pendenza di una funzione è zero in x, e la derivata seconda in x è:
- meno di 0, è un massimo locale
- maggiore di 0, è un minimo locale
- uguale a 0, allora il test fallisce (ci possono essere altri modi per scoprirlo)
“Derivata seconda: meno di 0 è un massimo, maggiore di 0 è un minimo”
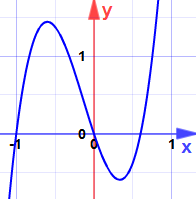
esempio: Trova i massimi e i minimi per:
y = 5×3 + 2×2 – 3x
La derivata (pendenza) è:
![]() y = 15×2 + 4x – 3
y = 15×2 + 4x – 3
Che è quadratica con zeri a:
- x = -3/5
- x = +1/3
Potrebbero essere massimi o minimi? (Non guardare ancora il grafico!)
La derivata seconda è y”= 30x + 4
Alla x = -3/5:
Alla x = +1/3:
(Ora puoi guardare il grafico.)
Parole
Un punto alto è chiamato massimo (plurale maxima).
Un punto basso è chiamato minimo (plurale minima).
La parola generale per massimo o minimo è extremum (plurale extrema).
Si dice massimo (o minimo) locale quando ci possono essere punti più alti (o più bassi) altrove ma non nelle vicinanze.
Un altro esempio
Esempio: Trova i massimi e i minimi per:
y = x3 – 6×2 + 12x – 5
La derivata è:
![]() y = 3×2 – 12x + 12
y = 3×2 – 12x + 12
Che è quadratica con un solo zero a x = 2
È un massimo o un minimo?
La derivata seconda è y” = 6x – 12
Alla x = 2:
Ecco perché:
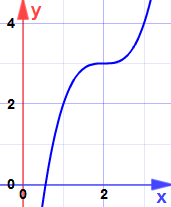
È un punto di sella … la pendenza diventa zero, ma non è né massimo né minimo.
Deve essere differenziabile
E c’è un importante punto tecnico:
La funzione deve essere differenziabile (la derivata deve esistere in ogni punto del suo dominio).
Esempio: Che ne dite della funzione f(x) = |x| (valore assoluto) ?
| |x| appare così: |  |
Alla x=0 ha un cambiamento molto appuntito!
Infatti non è differenziabile lì (come mostrato nella pagina dei differenziabili).
Quindi non possiamo usare questo metodo per la funzione valore assoluto.
La funzione deve anche essere continua, ma ogni funzione che è differenziabile è anche continua, quindi non c’è bisogno di preoccuparsene.




0 commenti