Recentemente, mentre scrivevamo il nostro libro Numericon, ci siamo imbattuti in quello che ora è diventato uno dei nostri numeri preferiti: Il numero di Graham. Uno dei motivi per cui lo amiamo è che questo numero è grande. In realtà, questo è un eufemismo. Il numero di Graham è incredibilmente grande.

L’universo osservabile è grande, ma il numero di Graham è più grande. Immagine: ESA e Planck Collaboration.
Il nostro nuovo numero preferito è più grande dell’età dell’Universo, sia misurata in anni (circa 14 miliardi di anni) che in secondi (4,343×1017 secondi). È più grande del numero di Avogadro, un considerevole 6,02214129 x 1023. Questo è il numero di atomi di idrogeno in 1 grammo di idrogeno, che si chiama mole ed è l’unità standard per misurare una quantità di una sostanza in chimica o fisica.
Il numero di Graham è più grande del numero di atomi nell’Universo osservabile, che si pensa sia tra 1078 e 1082. È più grande del 48° primo di Mersenne,
257.885.161-1,
il più grande numero primo che conosciamo, che ha ben 17.425.170 cifre. Ed è più grande del famoso googol, 10100 (un 1 seguito da 100 zeri), che fu definito nel 1929 dal matematico americano Edward Kasner e nominato da suo nipote di nove anni, Milton Sirotta. (Questo potrebbe suonare familiare, dato che Google ha preso il nome da questo numero, anche se hanno sbagliato l’ortografia).
Il numero di Graham è anche più grande di un googolplex, che Milton inizialmente definiva come un 1, seguito dalla scrittura di zeri fino a stancarsi, ma che ora è comunemente accettato come 10googol=10(10100). Un googleplex è significativamente più grande del 48° primo di Mersenne. Voi, o piuttosto un computer, potete scrivere il 48° primo di Mersenne nella sua interezza, tutte le 17.425.170 cifre. Ma, nonostante il fatto che io possa dirvi qual è ogni cifra del googolplex (la prima è un 1, le altre sono tutte 0), nessuna persona, nessun computer, nessuna civiltà sarà mai in grado di scriverlo per intero. Questo perché non c’è abbastanza spazio nell’Universo per scrivere tutte le googol+1 cifre di un googolplex. Come Kasner, e il suo collega James Newman, dissero del googolplex (nel loro meraviglioso libro del 1940 Mathematics and the imagination che introdusse il mondo a questi numeri): “Si può avere un’idea delle dimensioni di questo numero molto grande ma finito dal fatto che non ci sarebbe abbastanza spazio per scriverlo, se si andasse alla stella più lontana, facendo il giro di tutte le nebulose e mettendo zeri ad ogni centimetro del percorso”.
Il numero di Graham è più grande del googolplex. È così grande che l’universo non contiene abbastanza materiale su cui scrivere le sue cifre: è letteralmente troppo grande da scrivere. Ma questo numero è finito, è anche un numero intero, e nonostante sia così incredibilmente grande sappiamo che è divisibile per 3 e finisce con un 7.
Una grande festa
Le origini del numero di Graham risalgono al 1928 quando un giovane e brillante matematico, Frank Ramsey, notò una cosa sorprendente mentre stava lavorando a un articolo sulla logica: il disordine completo sembrava essere impossibile. Non importa quanto sia complicato il vostro sistema, sacche di ordine di qualsiasi dimensione sono sempre garantite se il sistema è abbastanza grande.
Questo risultato, che era solo una piccola parte del particolare articolo su cui stava lavorando, fu l’inizio di un intero nuovo campo della matematica chiamato Teoria di Ramsey. Questo settore della matematica viene spesso spiegato con l’esempio di una festa. Supponiamo che stai dando una festa e vuoi essere sicuro di invitare un buon mix di persone e decidi di tenere traccia di chi conosce chi. Supponete di disegnare una mappa delle relazioni di tutti i vostri amici, collegando due persone con un bordo blu se sono amici e con un bordo rosso se sono estranei. Allora potreste ritrovarvi con qualcosa del genere:
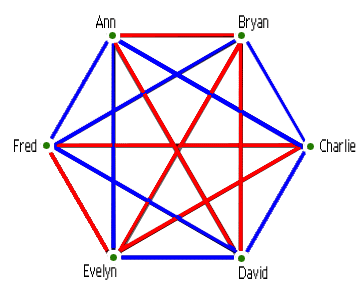
Ora questo sembra piuttosto complicato e ci vorrebbero molte informazioni per descrivere chi è collegato con i bordi rossi e chi con quelli blu. Ma se si zooma solo su Ann, Bryan e David, sono tutti collegati da bordi rossi. Questo triangolo rosso è un esempio di ordine che si nasconde nella disordinata rete generale. Più un sistema è ordinato, più semplice è la sua descrizione. La rete di amicizia più ordinata è quella che ha tutti i bordi dello stesso colore: cioè, tutti sono amici o tutti sono estranei.
Ramsey ha scoperto che non importa quanto ordine si stia cercando – che si tratti di tre persone che sono tutti amici e sconosciuti o di venti persone che sono tutti amici e sconosciuti – è garantito trovarlo finché il sistema in cui si sta cercando è abbastanza grande. Per garantirsi un gruppo di tre persone tutte amiche o tutte estranee occorre una rete di amicizia di sei persone: cinque persone non bastano, come dimostra questo controesempio.
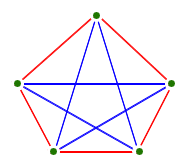
Il numero di persone di cui avete bisogno per garantirvi di trovare tre amici o tre sconosciuti si chiama numero di Ramsey R(3,3). Conosciamo alcuni numeri di Ramsey: abbiamo visto che R(3,3)=6, ed è stato dimostrato che R(4,4), il numero di persone di cui hai bisogno per garantire che troverai quattro amici o quattro sconosciuti, è 18. Ma ci scontriamo con un muro molto rapidamente. Per esempio non sappiamo cosa sia R(5,5). Sappiamo che è da qualche parte tra 43 e 49, ma è il massimo che possiamo ottenere per ora.
Parte del problema è che i numeri nella teoria di Ramsey crescono incredibilmente grandi molto rapidamente. Se stiamo guardando le relazioni tra tre persone, la nostra rete ha solo tre bordi e ci sono ragionevolmente 23 modi possibili di colorare la rete. Per quattro persone ci sono sei bordi e 26=64 colorazioni possibili. Ma per le relazioni tra sei persone ci sono quindici bordi e dobbiamo già considerare un ingombrante 215=32.768 possibili colorazioni. I matematici sono abbastanza sicuri che R(5,5) sia uguale a 43 ma non hanno trovato un modo per dimostrarlo. Un’opzione sarebbe quella di controllare tutte le possibili colorazioni per una rete di 43 persone. Ma ognuna di queste ha 903 bordi, quindi bisognerebbe controllare tutte le 2903 colorazioni possibili – più colorazioni di quanti atomi ci siano nell’Universo osservabile!
Troppo grande da scrivere ma non troppo grande per Graham
I grandi numeri hanno sempre fatto parte della teoria di Ramsey, ma nel 1971 il matematico Ronald Graham se ne uscì con un numero che nacque prima di lui. Stabilì un limite superiore per un problema nell’area che era, all’epoca, il più grande numero esplicitamente definito mai pubblicato. Piuttosto che disegnare reti di relazioni tra persone su un pezzo di carta piatto come abbiamo fatto finora, Graham era interessato a reti in cui le persone erano sedute sugli angoli di un cubo.

In questa immagine possiamo vedere che per una particolare fetta diagonale piatta del cubo, quella che contiene quattro degli angoli, tutti i bordi sono rossi. Ma non tutte le colorazioni di un cubo tridimensionale hanno una tale fetta monocolore. Fortunatamente, però, i matematici hanno anche un modo di pensare ai cubi di dimensioni superiori. Più alta è la dimensione, più angoli ci sono: un cubo tridimensionale ha 8 angoli, un cubo quadridimensionale ha 16 angoli, un cubo a cinque dimensioni ha 32 angoli e così via. Graham voleva sapere quanto grande doveva essere la dimensione del cubo per garantire l’esistenza di una fetta monocolore.

Ronald Graham che ci ha dato il suo bel numero. Immagine: Cheryl Graham.
Graham è riuscito a trovare un numero che garantiva l’esistenza di una tale fetta per un cubo di quella dimensione. Ma questo numero, come abbiamo detto prima, era assolutamente enorme, così grande da essere troppo grande per essere scritto all’interno dell’Universo osservabile. Graham fu comunque in grado di definire esplicitamente questo numero usando una notazione ingegnosa chiamata notazione a frecce che estende le nostre comuni operazioni aritmetiche di addizione, moltiplicazione ed esponenziazione.
Possiamo pensare alla moltiplicazione come addizione ripetuta:
3 x 3 = 3+3+3
33 = 3 x 3 x 3.
Se definiamo la singola operazione della freccia, , come esponenziazione, allora:
33 = 33 = 3 x 3 x 3 = 27,
allora possiamo definire l’operazione della doppia freccia come
33 = 333 = 333 = 327 = 7.625.597.484.987.
Possiamo continuare a costruire nuove operazioni ripetendo quelle precedenti. La prossima sarebbe la tripla freccia
33 = 333 = 3(33)=37.625.597.484.987
una torre di potenze di 3 che è alta 7.625.597.484.987 livelli!
Il numero che è diventato noto come il numero di Graham (non il numero esatto che appariva nel suo documento iniziale, è un numero leggermente più grande e leggermente più facile da definire che spiegò a Martin Gardner poco dopo) è definito usando questa notazione con le frecce verso l’alto, in un processo cumulativo che crea torri di potenze di tre che vanno rapidamente a spirale oltre qualsiasi grandezza che possiamo immaginare.
Ma la cosa che ci piace del numero di Graham è che questa quantità inimmaginabilmente grande non è un concetto teorico: è un numero esatto. Sappiamo che è un numero intero, infatti è facile vedere che questo numero è un multiplo di tre per il modo in cui è definito come una torre di potenze di tre. E i matematici hanno imparato molto sui processi usati per definire il numero di Graham, compreso il fatto che una volta che una torre di potenze è abbastanza alta, le cifre decimali più a destra alla fine rimangono le stesse, non importa quanti altri livelli si aggiungono alla torre di potenze. Il numero di Graham può essere troppo grande da scrivere, ma sappiamo che finisce in sette. La matematica ha il potere non solo di definire l’inimmaginabile, ma anche di indagarlo.
Informazioni su questo articolo

Rachel Thomas e Marianne Freiberger sono le editrici di Plus. Questo articolo è un estratto del loro nuovo libro Numericon: A journey through the hidden lives of numbers.
0 commenti