Oltre ad esserci tanti fatti affascinanti sul pi greco, è anche il numero più studiato nella storia della matematica fino ad ora. Molte persone vogliono memorizzare le cifre del pi greco, non le cifre di altri numeri irrazionali (YouTube, PBS NewsHour). Spinge la gente alla follia e al caos. I matematici hanno lottato per secoli per calcolare esattamente pi greco.
Quindi, dovremmo smettere di lavorare su pi greco o dovremmo continuare a cercare un’approssimazione migliore? Assumere pi greco come uguale a 3,14 è abbastanza buono? O è sufficiente usare 40 cifre di pi greco per trovare la circonferenza della Via Lattea con un errore inferiore alla dimensione di un protone (JPL NASA)? Le prime 152 cifre sono sufficienti per trovare la circonferenza dell’universo osservabile a 93 miliardi di anni luce (WIRED)? Ci sono centinaia di matematici che da anni cercano di capire altre cifre di pi greco. È come cercare di arrivare alla luna e poi al pianeta successivo, e così via… Ma perché? Perché i matematici si preoccupano di calcolare altre cifre? Perché 34,1 trilioni di cifre di pi greco non sono sufficienti? È perché il pi greco si annida in ogni cerchio?
La ragione logica sembra criptica; è perché pi greco è una bella fonte per generare numeri casuali. Tuttavia, la vera ragione sembra essere così che i paesi possono mostrare la loro tecnologia agli altri paesi, perché calcolare trilioni di cifre di pi greco ha bisogno di un computer molto potente. Per esempio, nell’episodio di Star Trek “Wolf in the Fold”, Spock sventa il computer malvagio ordinandogli di “calcolare fino all’ultima cifra il valore di Pi greco”. Quindi chiedere a un computer di calcolare il Pi greco è chiamato “uno stress test”, e può farlo andare in crash.
D’altra parte, noi umani siamo creatori maldestri. Stare a casa a bere il tè è una bella attività, ma quando ci annoiamo cerchiamo di scalare la più alta delle montagne, di sconfiggere una tigre o di memorizzare le cifre del pi greco come Chao Lu, che ha memorizzato correttamente le prime 67.890 cifre del pi greco. Continueremo a fare queste cose perché ci piace capire il mondo che ci circonda.
Il 12 settembre 1962, John F. Kennedy fece un discorso sul programma spaziale. Disse:
“Non c’è ancora nessuna lotta, nessun pregiudizio, nessun conflitto nazionale nello spazio esterno. I suoi pericoli sono ostili a tutti noi. La sua conquista merita il meglio di tutta l’umanità, e la sua opportunità di cooperazione pacifica non si ripresenta mai più. Ma perché, dicono alcuni, la luna? Perché scegliere questo come obiettivo? E potrebbero chiedersi: perché scalare la montagna più alta? Abbiamo scelto di andare sulla luna. Scegliamo di andare sulla luna in questo decennio e di fare le altre cose, non perché sono facili, ma perché sono difficili, perché quell’obiettivo servirà a organizzare e misurare il meglio delle nostre energie e capacità, perché quella sfida è una sfida che siamo disposti ad accettare, una sfida che non siamo disposti a rimandare, e una sfida che intendiamo vincere, e anche le altre.
Siamo inevitabilmente legati al passato, e pi è un filo che ha attraversato tutta la storia umana. Ecco perché possiamo dire che finché ci saranno persone, ci sarà sempre qualcuno che si chiederà cosa ci sarà dopo. E vi assicuro che da qualche parte nel mondo c’è un matematico o uno scienziato che usa il pi greco per qualcosa di importante per il nostro universo perché il pi greco è ancora la misteriosa costante della natura.
L’affermazione precedente è assolutamente vera perché c’è sempre stato qualcuno che lavora sul pi greco. La matematica è vecchia come la civiltà. Il Pi greco è stato studiato dalla razza umana per quasi 4000 anni. Quando gli ultimi mammut si stavano estinguendo, la gente studiava il Pi greco. Per quanto ne sappiamo, Archimede dell’antica Grecia fu uno dei primi esseri umani a calcolare il pi greco, molto probabilmente aiutando i costruttori di ruote. Ma come fece a stimare il valore di pi greco?
In primo luogo, vide che tutti i poligoni sono un cerchio. Secondo Archimede, se si continua ad aumentare il numero dei lati di un poligono, ci si avvicina al cerchio perfetto. In altre parole, un pentagono è più cerchio di un quadrato, ma un esagono è più cerchio di un pentagono, e così via… Così, il leggendario matematico Archimede definì un cerchio come un poligono regolare con un numero estremamente grande di lati più di duemila anni fa.
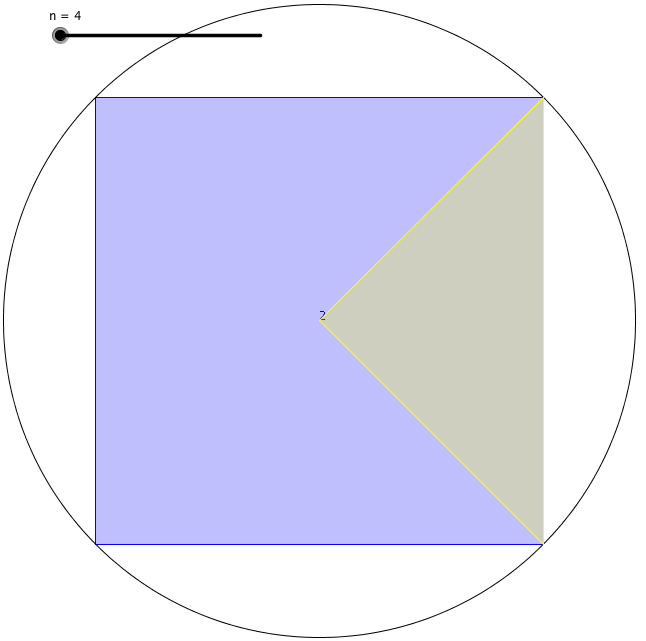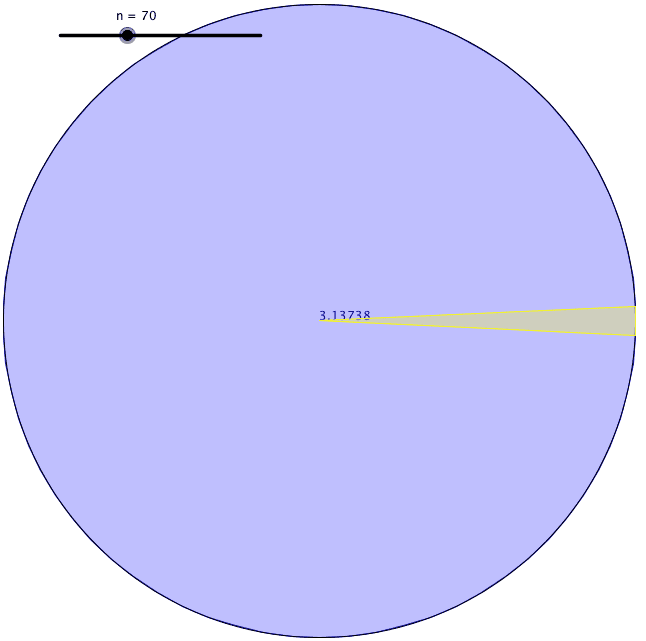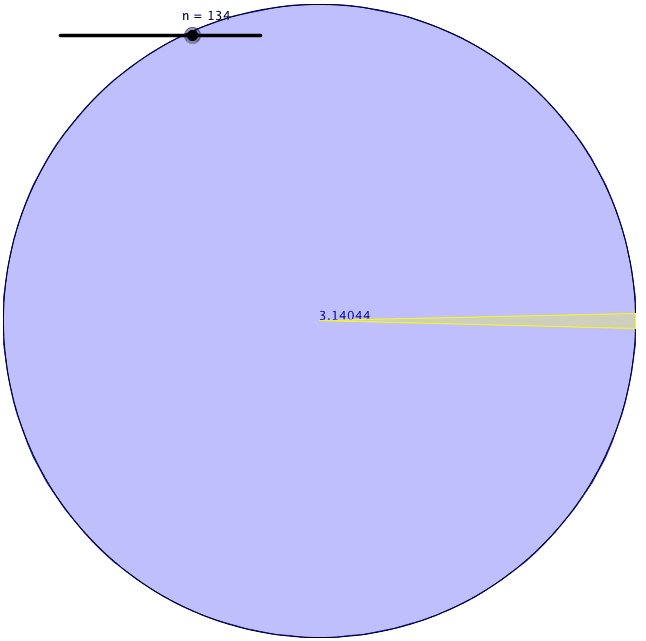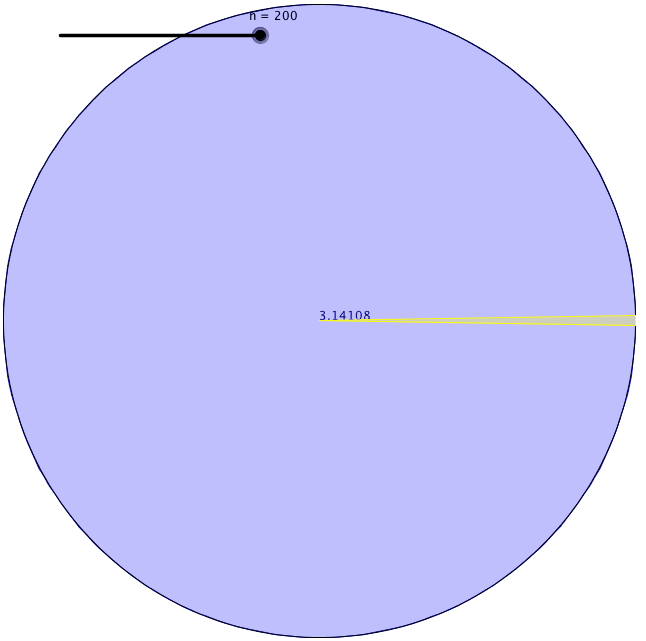
La sua definizione è utile perché misurare una superficie curva era difficile da fare con precisione. Ha trovato un modo per trovare la circonferenza di un cerchio. Per prima cosa, disegnò un quadrato con i suoi angoli che toccavano il perimetro di un cerchio e trovò il perimetro del quadrato inscritto. In secondo luogo, disegnò un altro quadrato con i suoi lati che toccavano il perimetro del cerchio e trovò il perimetro del quadrato circoscritto. Arrivò alla conclusione che la circonferenza del cerchio doveva trovarsi da qualche parte tra il valore di questi due perimetri di quadrati.
Utilizzando questo metodo, tuttavia, la differenza tra questi due valori era piuttosto grande quando usava i quadrati. Così, disegnò dei pentagoni per vedere i limiti superiore e inferiore della circonferenza del cerchio. In quel momento ottenne una gamma più piccola di limiti. In seguito, ha continuato ad aumentare il numero di facce del poligono che stava disegnando dentro e fuori il cerchio. Ogni volta che lo faceva, la sua stima diventava più accurata. Archimede arrivò a un poligono regolare di 96 facce, finché non si esaurì. Il limite inferiore e superiore che trovò quella volta furono 3,1408 e 3,1429. Così, calcolò π con due cifre decimali.
Il metodo di Archimede doveva essere migliorato perché la sua vita non sarebbe stata abbastanza lunga per trovare le altre cifre di pi greco a mano. I matematici dovevano scoprire formule più efficienti e nuove tecniche.
Prima di poterlo fare, dovevano scoprire l’algebra. All’inizio, la gente usava i segni per le cifre. Per esempio, diciamo che tu e il tuo vicino avete 75 cavalli insieme e tu hai 35 cavalli. Devi trovare il numero dei cavalli che ha il tuo vicino. Senza l’algebra, la soluzione richiederebbe molto tempo. Ma dopo la scoperta dell’algebra, usiamo semplicemente le equazioni per risolvere i problemi. In questo esempio specifico, possiamo scrivere 75 = x + 35 dove x è il numero di cavalli del tuo vicino. Scrivere una tale equazione e usare una variabile invece di un numero è stato rivoluzionario per il mondo classico. L’algebra ha permesso calcoli molto più facili in tutta la matematica.
L’adozione dell’algebra da parte dei grandi matematici ha ispirato un modo completamente nuovo di guardare il mondo. Il successivo grande salto nel calcolo del pi greco fu l’invenzione del calcolo. Dopo di che, i matematici hanno iniziato a lavorare sulle serie infinite. Una serie infinita è un’espressione con numeri aggiunti uno dopo l’altro fino all’infinito, e a volte queste serie infinite convergono verso un particolare valore.
Oggi ci sono molti metodi disponibili per calcolare il Pi greco. Gottfried Leibniz ha trovato pi greco all’infinito. James Gregory ha trovato l’equazione sottostante per pi greco. Stava lavorando su una delle sorprendenti serie infinite per la funzione tangente inversa qui sotto. Ha aggiunto infinitamente molti piccoli numeri insieme e ha trovato pi greco.
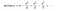
Ha messo x = 1 nella serie tangente inversa.serie tangente. Ci ha mostrato che più si va avanti, più ci si avvicina alla stima di pi greco. Tuttavia, per ottenere 10 cifre di pi greco, dobbiamo scrivere circa 5 miliardi di frazioni da sommare.
0 commenti