La legge di Hess

Perché funziona

Una visione pittorica della legge di Hess applicata al calore di equazione è illustrativa. Nella figura 1, i reagenti C(s) + 2 H2O(g) sono messi insieme in una scatola, che rappresenta lo stato dei materiali coinvolti nella reazione prima della reazione. I prodotti CO2(g) + 2 H2(g) sono messi insieme in una seconda scatola che rappresenta lo stato dei materiali coinvolti dopo la reazione. La freccia di reazione che collega queste scatole è etichettata con il calore di questa reazione. Ora prendiamo questi stessi materiali e li mettiamo in una terza scatola contenente C(s), O2(g), e 2 H2(g). Questa scatola è collegata alle scatole del reagente e del prodotto con frecce di reazione, etichettate con i calori di reazione nell’equazione e nell’equazione .

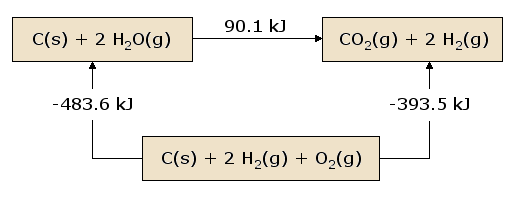
Questa immagine della legge di Hess rivela che il calore di reazione lungo il “percorso” che collega direttamente lo stato di reagente allo stato di prodotto è esattamente uguale al calore totale di reazione lungo il “percorso” alternativo che collega i reagenti ai prodotti attraverso lo stato intermedio contenente \(C_{(s)}}, \(O_{2(g)\ e 2 \(H_{2(g)\). Una conseguenza della nostra osservazione della legge di Hess è quindi che il calore netto evoluto o assorbito durante una reazione è indipendente dal percorso che collega il reagente al prodotto (questa affermazione è di nuovo soggetta alla nostra restrizione che tutte le reazioni nel percorso alternativo devono avvenire in condizioni di pressione costante).

Una visione leggermente diversa della figura 1 risulta iniziando dalla scatola del reagente e seguendo un circuito completo attraverso le altre scatole che riportano alla scatola del reagente, sommando i calori netti di reazione mentre andiamo. Scopriamo che il calore netto trasferito (sempre a condizione che tutte le reazioni avvengano a pressione costante) è esattamente zero. Questa è un’affermazione della conservazione dell’energia: l’energia nello stato reagente non dipende dai processi che hanno prodotto quello stato. Pertanto, non possiamo estrarre alcuna energia dai reagenti con un processo che semplicemente ricrea i reagenti. Se così non fosse, potremmo produrre all’infinito quantità illimitate di energia seguendo il percorso circolare che riproduce continuamente i reagenti iniziali.

In base a questo ragionamento, possiamo definire una funzione energetica il cui valore per i reagenti è indipendente da come è stato preparato lo stato reagente. Allo stesso modo, il valore di questa funzione energetica nello stato prodotto è indipendente da come i prodotti sono stati preparati. Scegliamo questa funzione, H, in modo che la variazione della funzione, ΔH = Hprodotti – Hreagenti, sia uguale al calore di reazione q in condizioni di pressione costante. H, che chiamiamo entalpia, è una funzione di stato, poiché il suo valore dipende solo dallo stato dei materiali in esame, cioè la temperatura, la pressione e la composizione di questi materiali.

Il concetto di funzione di stato è in qualche modo analogo all’idea di elevazione. Consideriamo la differenza di elevazione tra il primo e il terzo piano di un edificio. Questa differenza è indipendente dal percorso che scegliamo per andare dal primo al terzo piano. Possiamo semplicemente salire due rampe di scale, o possiamo salire una rampa di scale, camminare per tutta la lunghezza dell’edificio e poi percorrere una seconda rampa di scale. Oppure possiamo prendere l’ascensore. Possiamo anche uscire e farci sollevare da una gru fino al tetto dell’edificio, da cui scendiamo al terzo piano. Ogni percorso produce esattamente lo stesso dislivello, anche se la distanza percorsa è significativamente diversa da un percorso all’altro. Questo semplicemente perché l’elevazione è una “funzione di stato”. La nostra elevazione, stando al terzo piano, è indipendente da come siamo arrivati al terzo piano, e lo stesso vale per il primo piano. Poiché l’elevazione è quindi una funzione di stato, il guadagno di elevazione è indipendente dal percorso. Ora, l’esistenza di una funzione di stato energetica H è di notevole importanza nel calcolo dei calori di reazione. Consideriamo la reazione prototipo nella sottofigura 2.1, con i reagenti R che vengono convertiti in prodotti P. Vogliamo calcolare il calore assorbito o rilasciato in questa reazione, che è ΔH. Poiché H è una funzione di stato, possiamo seguire qualsiasi percorso da R a P e calcolare ΔH lungo quel percorso. Nella sottofigura 2.2, consideriamo uno di questi possibili percorsi, che consiste in due reazioni che passano attraverso uno stato intermedio che contiene tutti gli atomi coinvolti nella reazione, ciascuno in forma elementare. Questo è uno stato intermedio utile perché può essere usato per ogni possibile reazione chimica. Per esempio, nella figura 1, gli atomi coinvolti nella reazione sono C, H e O, ognuno dei quali è rappresentato nello stato intermedio in forma elementare. Possiamo vedere nella sottofigura 2.2 che il ΔH per la reazione complessiva è ora la differenza tra il ΔH nella formazione dei prodotti P dagli elementi e il ΔH nella formazione dei reagenti R dagli elementi.

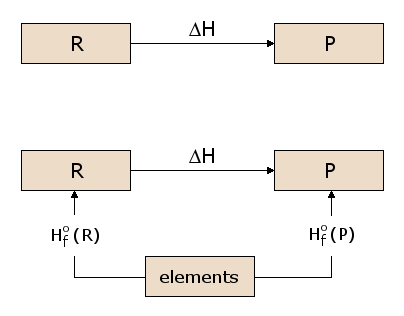
I valori di ΔH per la formazione di ogni materiale dagli elementi sono quindi di utilità generale nel calcolo del ΔH per qualsiasi reazione di interesse. Definiamo quindi la reazione di formazione standard per il reagente R, come

elementi allo stato standard R

e il calore coinvolto in questa reazione è l’entalpia standard di formazione, indicata da ΔHf°. Il pedice f, che sta per “formazione”, indica che il ΔH è per la reazione che crea il materiale dagli elementi allo stato standard. Il pedice ° indica che le reazioni avvengono in condizioni di pressione standard costante di 1 atm. Dalla sottofigura 2.2, vediamo che il calore di qualsiasi reazione può essere calcolato da

Sono state compilate ampie tabelle di valori di ΔH°f (Tabella T1) che ci permettono di calcolare con completa sicurezza il calore di reazione per qualsiasi reazione di interesse, anche includendo reazioni ipotetiche che possono essere difficili da eseguire o impossibilmente lente a reagire.