KDnuggets

A prescindere dalla tua posizione sulla questione della sensualità della Data Science, è semplicemente impossibile ignorare la continua importanza dei dati e la nostra capacità di analizzarli, organizzarli e contestualizzarli. Attingendo ai loro vasti archivi di dati sull’occupazione e al feedback dei dipendenti, Glassdoor ha classificato il Data Scientist al primo posto nella sua lista dei 25 migliori lavori in America. Quindi il ruolo è qui per rimanere, ma senza dubbio, le specifiche di ciò che fa un Data Scientist si evolveranno. Con tecnologie come il Machine Learning che diventano sempre più comuni, e campi emergenti come il Deep Learning che guadagnano una trazione significativa tra i ricercatori e gli ingegneri – e le aziende che li assumono – gli scienziati dei dati continuano a cavalcare la cresta di un’incredibile onda di innovazione e progresso tecnologico.

Mentre avere una forte capacità di codifica è importante, la scienza dei dati non è solo ingegneria del software (in effetti, avere una buona familiarità con Python e si è pronti a partire). Gli scienziati dei dati vivono all’intersezione di codifica, statistica e pensiero critico. Come ha detto Josh Wills, “lo scienziato dei dati è una persona che è meglio in statistica di qualsiasi programmatore e meglio in programmazione di qualsiasi statistico”. Personalmente conosco troppi ingegneri del software che cercano di trasformarsi in data scientist e utilizzano ciecamente framework di apprendimento automatico come TensorFlow o Apache Spark per i loro dati senza una comprensione approfondita delle teorie statistiche dietro di loro. Ecco quindi lo studio dell’apprendimento statistico, un quadro teorico per l’apprendimento automatico che attinge dai campi della statistica e dell’analisi funzionale.

Perché studiare l’apprendimento statistico? È importante capire le idee dietro le varie tecniche, per sapere come e quando usarle. Si devono capire prima i metodi più semplici, per comprendere quelli più sofisticati. È importante valutare accuratamente le prestazioni di un metodo, per sapere quanto bene o male sta funzionando. Inoltre, questa è un’area di ricerca eccitante, con importanti applicazioni nella scienza, nell’industria e nella finanza. In definitiva, l’apprendimento statistico è un ingrediente fondamentale nella formazione di un moderno scienziato dei dati. Esempi di problemi di apprendimento statistico includono:

• Identificare i fattori di rischio per il cancro alla prostata.
• Classificare un fonema registrato sulla base di un log-periodogramma.
• Prevedere se qualcuno avrà un attacco di cuore sulla base di misure demografiche, dietetiche e cliniche.
• Personalizzare un sistema di rilevamento dello spam via email.
• Identificare i numeri in un codice postale scritto a mano.
• Classificare un campione di tessuto in una delle varie classi di cancro.
• Stabilire la relazione tra lo stipendio e le variabili demografiche nei dati dei sondaggi sulla popolazione.

Nel mio ultimo semestre di università, ho fatto uno studio indipendente sul Data Mining. La classe copre materiali espansivi provenienti da 3 libri: Intro to Statistical Learning (Hastie, Tibshirani, Witten, James), Doing Bayesian Data Analysis (Kruschke), e Time Series Analysis and Applications (Shumway, Stoffer). Abbiamo fatto molti esercizi su Analisi Bayesiana, Markov Chain Monte Carlo, Modellazione Gerarchica, Apprendimento Supervisionato e Non Supervisionato. Questa esperienza approfondisce il mio interesse nel campo accademico del Data Mining e mi convince a specializzarmi ulteriormente in esso. Recentemente, ho completato il corso online di Apprendimento Statistico su Stanford Lagunita, che copre tutto il materiale del libro Intro to Statistical Learning che ho letto nel mio studio indipendente. Essendo ora esposto al contenuto due volte, voglio condividere le 10 tecniche statistiche dal libro che credo che ogni scienziato dei dati dovrebbe imparare per essere più efficace nella gestione di grandi insiemi di dati.

Prima di andare avanti con queste 10 tecniche, voglio differenziare tra apprendimento statistico e apprendimento automatico. Ho scritto uno dei più popolari post di Medium sull’apprendimento automatico prima, quindi sono sicuro di avere l’esperienza per giustificare queste differenze:

• L’apprendimento automatico è nato come un sottocampo dell’Intelligenza Artificiale.
• L’apprendimento statistico è nato come un sottocampo della Statistica.
• L’apprendimento automatico ha una maggiore enfasi sulle applicazioni su larga scala e sulla precisione di previsione.
• L’apprendimento statistico enfatizza i modelli e la loro interpretabilità, e la precisione e l’incertezza.
• Ma la distinzione è diventata sempre più sfumata, e c’è una grande quantità di “cross-fertilization.”
• Il machine learning ha il sopravvento nel marketing!

1 – Regressione lineare:

In statistica, la regressione lineare è un metodo per prevedere una variabile target adattando la migliore relazione lineare tra la variabile dipendente e quella indipendente. Il miglior adattamento è fatto assicurandosi che la somma di tutte le distanze tra la forma e le osservazioni reali in ogni punto sia la più piccola possibile. L’adattamento della forma è “migliore” nel senso che nessun’altra posizione produrrebbe meno errori data la scelta della forma. 2 tipi principali di regressione lineare sono la regressione lineare semplice e la regressione lineare multipla. La Regressione Lineare Semplice utilizza una singola variabile indipendente per prevedere una variabile dipendente adattando una relazione lineare migliore. La Regressione Lineare Multipla usa più di una variabile indipendente per predire una variabile dipendente adattando la migliore relazione lineare.

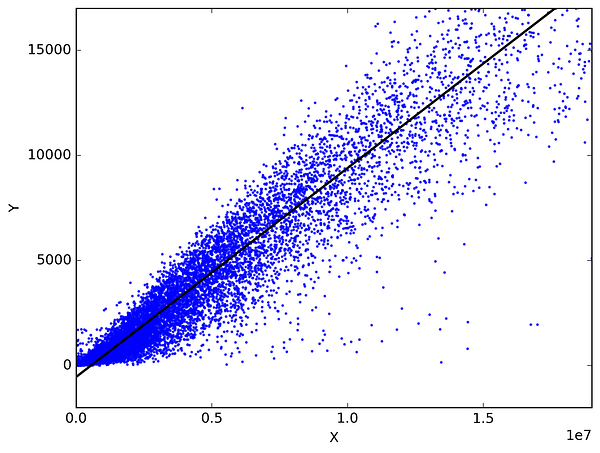
Scegliete 2 cose che usate nella vostra vita quotidiana e che sono correlate. Ad esempio, ho i dati delle mie spese mensili, il reddito mensile e il numero di viaggi al mese per gli ultimi 3 anni. Ora ho bisogno di rispondere alle seguenti domande:

• Quale sarà la mia spesa mensile per il prossimo anno?
• Quale fattore (reddito mensile o numero di viaggi al mese) è più importante nel decidere la mia spesa mensile?
• Come il reddito mensile e i viaggi al mese sono correlati alla spesa mensile?

2 – Classificazione:

La classificazione è una tecnica di data mining che assegna categorie a un insieme di dati al fine di aiutare in previsioni e analisi più accurate. Chiamata anche albero delle decisioni, la classificazione è uno dei diversi metodi destinati a rendere efficace l’analisi di serie di dati molto grandi. Si distinguono 2 principali tecniche di classificazione: Regressione logistica e Analisi discriminante.

La Regressione logistica è l’analisi di regressione appropriata da condurre quando la variabile dipendente è dicotomica (binaria). Come tutte le analisi di regressione, la regressione logistica è un’analisi predittiva. La regressione logistica è usata per descrivere i dati e per spiegare la relazione tra una variabile dipendente binaria e una o più variabili indipendenti a livello nominale, ordinale, di intervallo o di rapporto. Tipi di domande che una regressione logistica può esaminare:

• Come cambia la probabilità di ammalarsi di cancro ai polmoni (Sì vs No) per ogni chilo in più di sovrappeso e per ogni pacchetto di sigarette fumato al giorno?

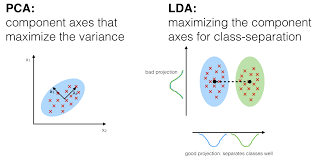
Nell’analisi discriminante, 2 o più gruppi o cluster o popolazioni sono noti a priori e 1 o più nuove osservazioni sono classificate in 1 delle popolazioni note in base alle caratteristiche misurate. L’analisi discriminante modella la distribuzione dei predittori X separatamente in ciascuna delle classi di risposta, e poi usa il teorema di Bayes per trasformarli in stime per la probabilità della categoria di risposta dato il valore di X. Tali modelli possono essere lineari o quadratici.

• L’analisi discriminante lineare calcola “punteggi discriminanti” per ogni osservazione per classificare in quale classe della variabile di risposta si trova. Questi punteggi sono ottenuti trovando combinazioni lineari delle variabili indipendenti. Assume che le osservazioni all’interno di ogni classe siano tratte da una distribuzione gaussiana multivariata e che la covarianza delle variabili predittive sia comune a tutti i k livelli della variabile di risposta Y.
• L’Analisi Discriminante Quadratica fornisce un approccio alternativo. Come LDA, QDA assume che le osservazioni di ogni classe di Y siano tratte da una distribuzione gaussiana. Tuttavia, a differenza di LDA, QDA assume che ogni classe abbia la propria matrice di covarianza. In altre parole, le variabili predittive non sono assunte per avere una varianza comune attraverso ciascuno dei k livelli in Y.

3 – Metodi di ricampionamento:

Il ricampionamento è il metodo che consiste nel prelevare campioni ripetuti dai campioni di dati originali. È un metodo non parametrico di inferenza statistica. In altre parole, il metodo di ricampionamento non comporta l’utilizzo di tabelle di distribuzione generiche per calcolare valori di probabilità p approssimati.

Il ricampionamento genera una distribuzione di campionamento unica sulla base dei dati reali. Utilizza metodi sperimentali, piuttosto che metodi analitici, per generare la distribuzione di campionamento unica. Produce stime imparziali poiché si basa su campioni imparziali di tutti i possibili risultati dei dati studiati dal ricercatore. Per comprendere il concetto di ricampionamento, è necessario capire i termini Bootstrapping e Cross-Validation:

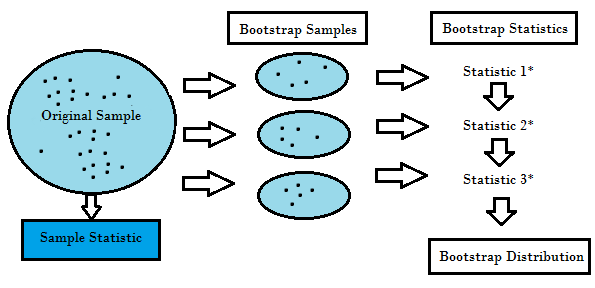
• Bootstrapping è una tecnica che aiuta in molte situazioni come la validazione delle prestazioni di un modello predittivo, metodi di ensemble, stima della distorsione e della varianza del modello. Funziona campionando con sostituzione dai dati originali, e prendere i punti di dati “non scelti” come casi di prova. Possiamo fare questo diverse volte e calcolare il punteggio medio come stima delle prestazioni del nostro modello.
• D’altra parte, la convalida incrociata è una tecnica per convalidare le prestazioni del modello, ed è fatta dividendo i dati di formazione in k parti. Prendiamo le k – 1 parti come il nostro set di allenamento e usiamo la parte “tenuta fuori” come set di test. Ripetiamo questo k volte in modo diverso. Infine, prendiamo la media dei k punteggi come stima delle nostre prestazioni.

Di solito per i modelli lineari, i minimi quadrati ordinari sono il criterio principale da considerare per adattarli ai dati. I prossimi 3 metodi sono approcci alternativi che possono fornire una migliore accuratezza di previsione e una migliore interpretabilità del modello per l’adattamento dei modelli lineari.

4 – Subset Selection:

Questo approccio identifica un sottoinsieme dei predittori p che riteniamo essere correlati alla risposta. Poi inseriamo un modello utilizzando i minimi quadrati delle caratteristiche del sottoinsieme.

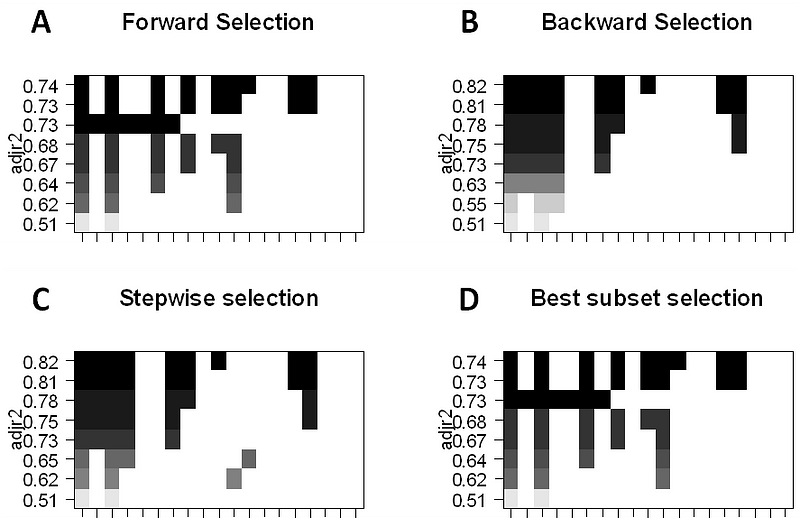
• Best-Subset Selection: Qui inseriamo una regressione OLS separata per ogni possibile combinazione dei predittori p e poi guardiamo i modelli risultanti. L’algoritmo è suddiviso in 2 fasi: (1) Adattare tutti i modelli che contengono k predittori, dove k è la lunghezza massima dei modelli, (2) Selezionare un singolo modello usando l’errore di predizione convalidato incrociato. È importante usare l’errore di test o di convalida, e non l’errore di addestramento per valutare l’adattamento del modello perché RSS e R² aumentano monotonamente con più variabili. L’approccio migliore è quello di effettuare la convalida incrociata e scegliere il modello con il più alto R² e il più basso RSS sulle stime dell’errore di test.
• Forward Stepwise Selection considera un sottoinsieme molto più piccolo di ppredittori. Inizia con un modello che non contiene predittori, poi aggiunge predittori al modello, uno alla volta fino a quando tutti i predittori sono nel modello. L’ordine delle variabili aggiunte è la variabile che dà il più grande miglioramento all’adattamento, fino a quando nessun’altra variabile migliora l’adattamento del modello usando l’errore di predizione cross-validato.
• Backward Stepwise Selection inizia con tutti i predittori p nel modello, poi rimuove iterativamente il predittatore meno utile uno alla volta.
• I metodi ibridi seguono l’approccio stepwise in avanti, tuttavia, dopo aver aggiunto ogni nuova variabile, il metodo può anche rimuovere le variabili che non contribuiscono al fit del modello.

5 – Shrinkage:

Questo approccio adatta un modello che coinvolge tutti i predittori p, tuttavia, i coefficienti stimati sono ridotti verso lo zero rispetto alle stime dei minimi quadrati. Questo restringimento, detto anche regolarizzazione, ha l’effetto di ridurre la varianza. A seconda del tipo di restringimento eseguito, alcuni dei coefficienti possono essere stimati esattamente a zero. Così questo metodo esegue anche la selezione delle variabili. Le due tecniche più conosciute per ridurre le stime dei coefficienti verso lo zero sono la regressione Ridge e il lasso.

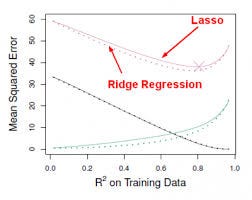
• La regressione Ridge è simile ai minimi quadrati, tranne che i coefficienti sono stimati minimizzando una quantità leggermente diversa. La regressione Ridge, come OLS, cerca le stime dei coefficienti che riducono RSS, tuttavia hanno anche una penalità di riduzione quando i coefficienti si avvicinano a zero. Questa penalità ha l’effetto di restringere le stime dei coefficienti verso lo zero. Senza entrare nella matematica, è utile sapere che la regressione di cresta restringe le caratteristiche con la più piccola varianza dello spazio di colonna. Come nell’analisi delle componenti principali, la regressione ridge proietta i dati nello spazio ddirezionale e quindi restringe i coefficienti delle componenti a bassa varianza più delle componenti ad alta varianza, che sono equivalenti alle componenti principali più grandi e più piccole.
• La regressione ridge ha almeno uno svantaggio: include tutti i predittori p nel modello finale. Il termine di penalità imposterà molti di loro vicino a zero, ma mai esattamente a zero. Questo non è generalmente un problema per l’accuratezza della previsione, ma può rendere il modello più difficile da interpretare i risultati. Lasso supera questo svantaggio ed è in grado di forzare alcuni dei coefficienti a zero se s è abbastanza piccolo. Poiché s = 1 risulta in una regolare regressione OLS, quando s si avvicina a 0 i coefficienti si riducono verso lo zero. Così, la regressione Lasso esegue anche la selezione delle variabili.