Il test F per l’analisi di regressione

Una procedura passo dopo passo per usare il test F

Per raggiungere gli obiettivi di cui sopra, seguiremo questi passi:

1. Formulare la statistica del test F, nota come statistica F.
2. Identificare la Funzione di Densità di Probabilità della variabile casuale che la statistica F rappresenta nell’ipotesi che l’ipotesi nulla sia vera.
3. Inserire i valori nella formula della statistica F e calcolare il valore di probabilità corrispondente usando la Funzione di Densità di Probabilità trovata nel passo 2. Questa è la probabilità di osservare il valore della statistica F assumendo che l’ipotesi nulla sia vera.
4. Se la probabilità trovata nel passo 3 è inferiore alla soglia di errore come 0,05, rifiutare l’ipotesi nulla e accettare l’ipotesi alternativa ad un livello di confidenza di (1,0 – soglia di errore), per esempio 1-0,05 = 0,95 (cioè il 95% di confidenza). Altrimenti, accettare l’ipotesi nulla con una probabilità di errore pari alla soglia di errore, per esempio a 0,05 o 5%.

Tuffiamoci in questi passi.

Passo 1: Sviluppare l’intuizione per la statistica del test

Ricordiamo che il test F misura quanto sia migliore un modello complesso rispetto a una versione più semplice dello stesso modello nella sua capacità di spiegare la varianza della variabile dipendente.

Consideriamo due modelli di regressione 1 e 2:

• Il modello 1 ha k_1 parametri. Il modello 2 ha k_2 parametri.
• Lascia che k_1 < k_2
• Quindi il modello 1 è la versione più semplice del modello 2. Cioè il modello 1 è il modello ristretto e il modello 2 è il modello non ristretto. Il modello 1 può essere annidato all’interno del modello 2.
• Lasciate che RSS_1 e RSS_2 siano la somma dei quadrati degli errori residui dopo che il modello 1 e il modello 2 sono adattati allo stesso set di dati.
• Lasciate che n sia il numero di campioni di dati.

Con le definizioni di cui sopra, la statistica del test F per la regressione può essere espressa come un rapporto come segue:

La formula della statistica F permette di calcolare quanta parte della varianza della variabile dipendente, il modello più semplice non è in grado di spiegare rispetto al modello complesso, espresso come frazione della varianza non spiegata dal modello complesso.

Nell’analisi di regressione, l’errore quadratico medio del modello montato è un’ottima misura della varianza non spiegata. Il che spiega i termini RSS nel numeratore e nel denominatore.

Il numeratore e il denominatore sono opportunamente scalati usando i corrispondenti gradi di libertà disponibili.

La statistica F è essa stessa una variabile casuale.

Determiniamo a quale Funzione di Densità di Probabilità obbedisce la statistica F.

Passo 2: Identificare la Funzione di Densità di Probabilità della statistica F

Si noti che sia il numeratore che il denominatore della statistica del test contengono le somme dei quadrati degli errori residui. Ricordate anche che nella regressione, l’errore residuo è una variabile casuale con una funzione di densità di probabilità (o massa di probabilità), cioè una PDF o PMF a seconda che sia continua o discreta. In questo caso ci interessa trovare la PDF della statistica F.

Se assumiamo che gli errori residui dei due modelli siano 1) indipendenti e 2) normalmente distribuiti, che casualmente sono requisiti della regressione Ordinaria ai minimi quadrati, allora si può vedere che il numeratore e il denominatore della formula della statistica F contengono somme di quadrati di variabili casuali indipendenti e normalmente distribuite.

Si può dimostrare che la somma dei quadrati di k variabili casuali indipendenti e normali segue la PDF della distribuzione Chi-quadrato(k).

Così il numeratore e il denominatore della formula F-statistica possono essere mostrati come versioni scalate di due distribuzioni chi-quadrato.

Con un po’ di matematica, si può anche dimostrare che il rapporto di due variabili casuali opportunamente scalate con distribuzione Chi-quadrato è esso stesso una variabile casuale che segue la distribuzione F, la cui PDF è mostrata qui sotto.

In altre parole:

Se la variabile casuale X ha la PDF della distribuzione F con parametri d_1 e d_2, cioè :

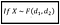
quindi, si può dimostrare che X è espresso come il rapporto di due variabili casuali opportunamente scalate X_1 e X_2, ciascuna delle quali ha la PDF di una distribuzione Chi-quadrato. Vale a dire :

Ora ricordiamo che k_1 e k_2 sono il numero di variabili nei modelli semplici e complessi M1 e M2 introdotti prima, e n è il numero di campioni di dati.

Sostituiamo d_1 e d_2 come segue:

d_1 = (k_2 – k_1) che è la differenza dei gradi di libertà dei residui dei due modelli M1 e M2 da confrontare, e

d_2 = (n – k_2) che sono i gradi di libertà dei residui del modello complesso M2,

Con queste sostituzioni, possiamo riscrivere la formula della distribuzione F come segue:

Confrontiamo la formula di cui sopra con la formula della statistica F (riprodotta qui sotto), dove sappiamo che il numeratore e il denominatore contengono PDF opportunamente scalate delle distribuzioni Chi-quadrato:

Confrontando queste due formule, è chiaro che:

1. Il grado di libertà ‘a’ della distribuzione Chi-quadrato al numeratore è (k1 – k2).
2. Il grado di libertà ‘b’ della distribuzione Chi-quadrato al denominatore è (n – k2).
3. La statistica del test F ha la stessa PDF della distribuzione F.

In altre parole, la statistica F segue la distribuzione F.

Passo 3: Calcolare il valore della statistica F

Se usate lo stimatore OLS di statsmodels, questo passo è un’operazione di una sola riga. Tutto quello che dovete fare è stampare OLSResults.summary() e otterrete:

1. il valore della statistica F e,
2. il corrispondente valore ‘p’, cioè la probabilità di incontrare questo valore, dalla PDF della distribuzione F.

La libreria statsmodels farà il lavoro pesante di entrambi i calcoli.

print(ols_results.summary())

Questo stampa quanto segue:

Passo 4: Determinare se l’ipotesi nulla può essere accettata

Siccome OLSResults.summary() stampa la probabilità che si verifichi la statistica F nell’ipotesi che l’ipotesi nulla sia vera, dobbiamo solo confrontare questa probabilità con il nostro valore alfa di soglia. Nel nostro esempio, il valore p restituito da .summary() è 4.84E-16 che è un numero estremamente piccolo. Molto più piccolo anche di alfa = 0,01. Quindi, c’è molto meno dell’1% di possibilità che la statistica F di 136,7 possa essersi verificata per caso sotto l’ipotesi di un’ipotesi nulla valida.

Quindi rifiutiamo l’ipotesi nulla e accettiamo l’ipotesi alternativa H_1 che il modello complesso, cioè il modello a variabili ritardate, nonostante i suoi ovvi difetti, sia in grado di spiegare la varianza della variabile dipendente Prezzo di chiusura meglio del modello a sola intercetta.