Lezione 4: Moltiplicare e dividere le frazioni
/it/fractions/adding-and-subtracting-fractions/content/
Moltiplicare le frazioni
Una frazione è una parte di un intero. Nell’ultima lezione hai imparato a sommare e sottrarre frazioni. Ma questo non è l’unico tipo di matematica che puoi fare con le frazioni. Ci sono momenti in cui sarà utile anche moltiplicare le frazioni.
Clicca sulla presentazione per imparare a scrivere un problema di moltiplicazione con le frazioni.
-

Facciamo un esempio di moltiplicazione con le frazioni. Supponiamo che tu beva 2/4 di un bricco di caffè ogni mattina.
-

Ma il tuo medico ti ha appena detto che devi ridurre il tuo consumo di caffè della metà.
-
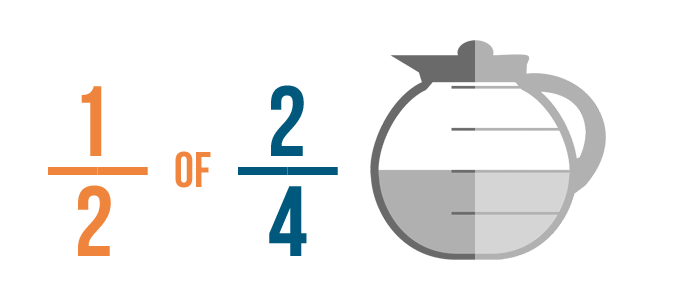
Ora devi capire quanto fa 1/2 di 2/4 di un bricco di caffè.
-
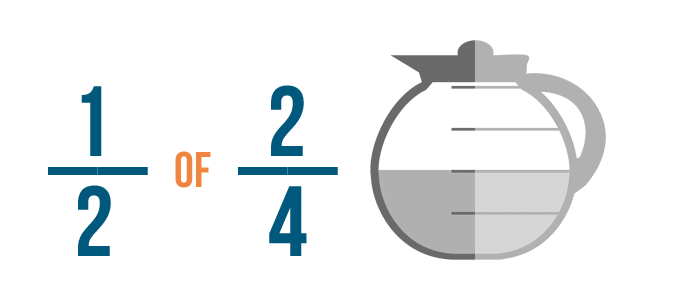
Questo potrebbe non sembrare un problema di moltiplicazione. Ma quando vedi la parola di con le frazioni, significa che devi moltiplicare.
-
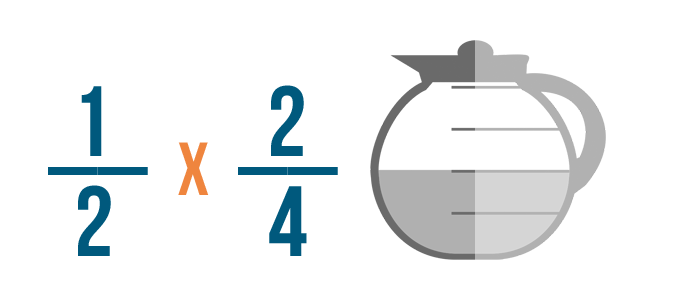
Per impostare l’esempio, sostituiremo semplicemente la parola di con un segno di moltiplicazione.
-
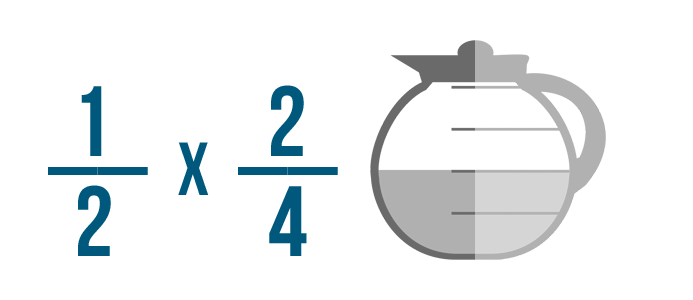
Ora il nostro esempio è pronto per essere risolto.
-
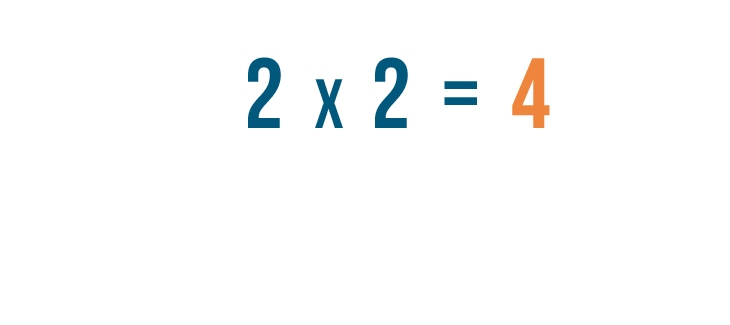
A differenza della moltiplicazione regolare, che dà un numero più grande…
-
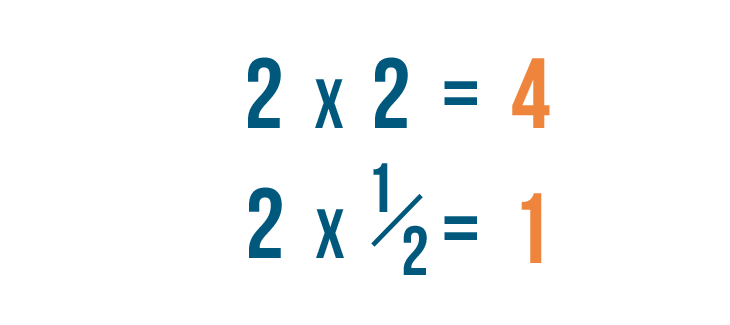
A differenza della moltiplicazione regolare, che ti dà un numero più grande… moltiplicando le frazioni di solito ti darà un numero più piccolo.
-
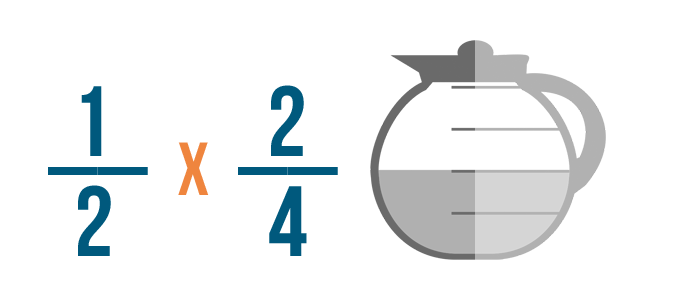
Quindi quando moltiplichiamo 1/2 per 2/4…
-

Quindi quando moltiplichiamo 1/2 per 2/4…la nostra risposta sarà più piccola di 2/4.
-
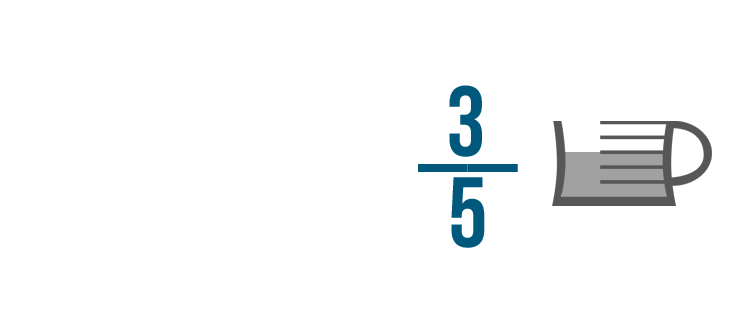
Ecco un altro esempio. Diciamo che hai 3/5 di una tazza di ripieno al cioccolato.
-
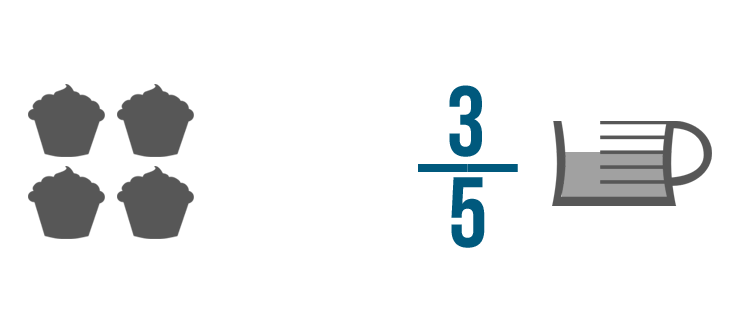
Vuoi mettere una quantità uguale di ripieno in ognuno di questi 4 cupcakes.
-
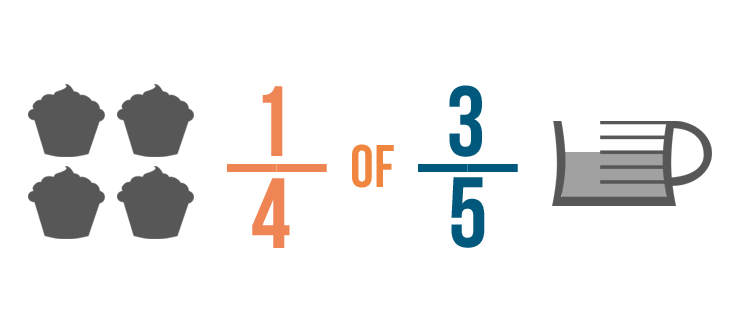
Si potrebbe dire che si vuole mettere 1/4 di 3/5 di una tazza di ripieno in ogni cupcake.
-
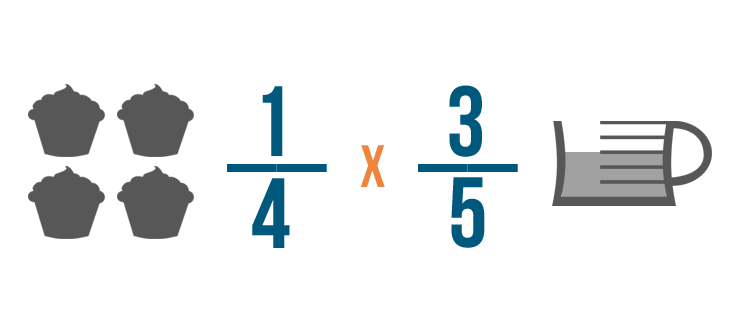
Come abbiamo fatto prima, cambieremo la parola di in un segno di moltiplicazione.
-
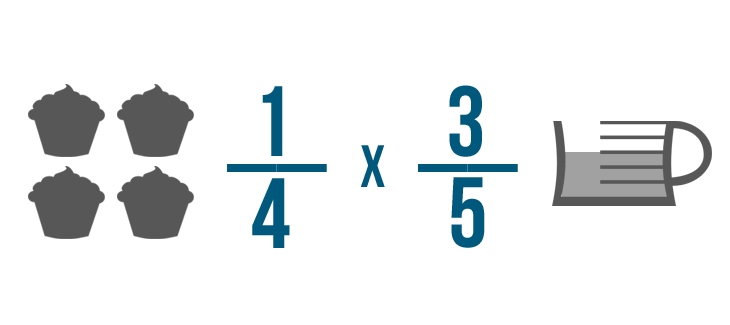
E ora le nostre frazioni sono pronte per essere moltiplicate.

Prova questo!
Prova a impostare il problema di moltiplicazione qui sotto. Non preoccuparti ancora di risolverlo!
Una ricetta richiede 2/3 di una tazza di latte. Vuoi tagliare la ricetta a metà.

Nota: Anche se il nostro esempio dice che la risposta corretta è 2/3 x 1/2, ricorda, con la moltiplicazione l’ordine non conta. Anche 1/2 x 2/3 sarebbe corretto.
Risolvere i problemi di moltiplicazione con le frazioni
Ora che sappiamo come impostare i problemi di moltiplicazione con le frazioni, esercitiamoci a risolverne alcuni. Se ti senti a tuo agio nel moltiplicare numeri interi, sei pronto per moltiplicare frazioni.
Clicca sulla presentazione per imparare a moltiplicare due frazioni.
-
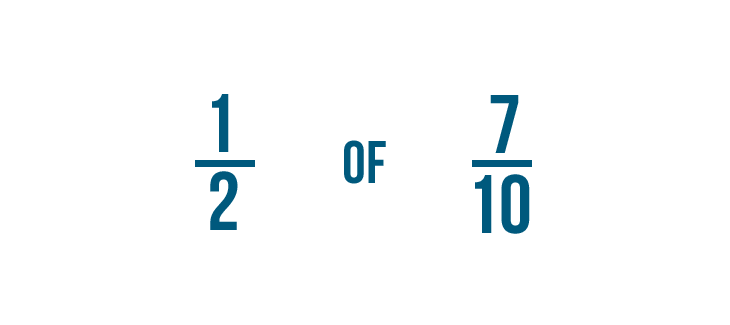
Moltipliciamo per trovare 1/2 di 7/10.
-
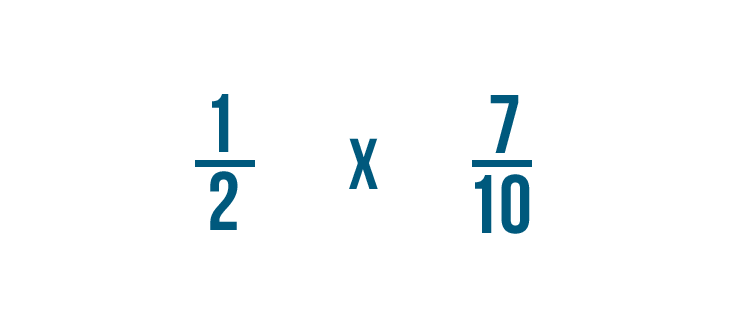
Come abbiamo fatto prima, sostituiamo la parola di con un segno di moltiplicazione. Ora siamo pronti a moltiplicare.
-
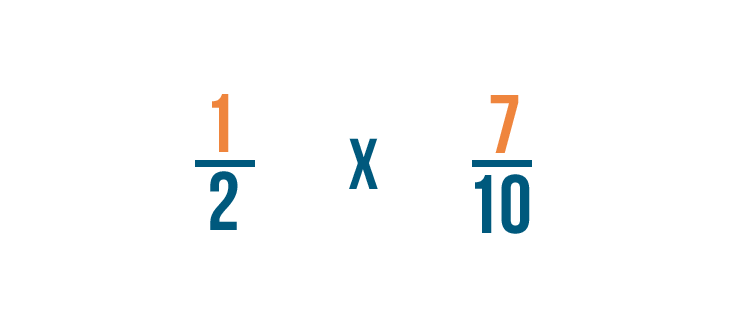
Per prima cosa, moltiplichiamo i numeratori: 1 e 7.
-
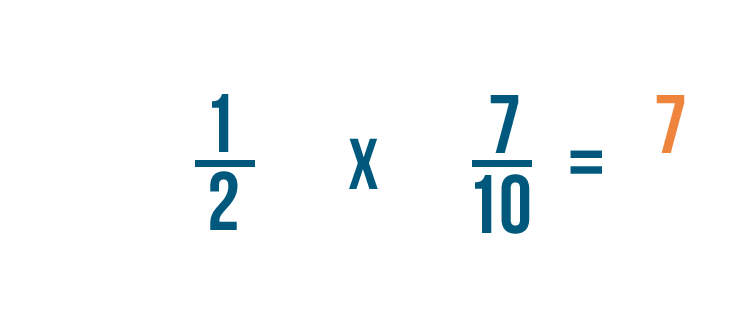
1 per 7 è uguale a 7, quindi scriveremo 7 a destra dei numeratori.
-
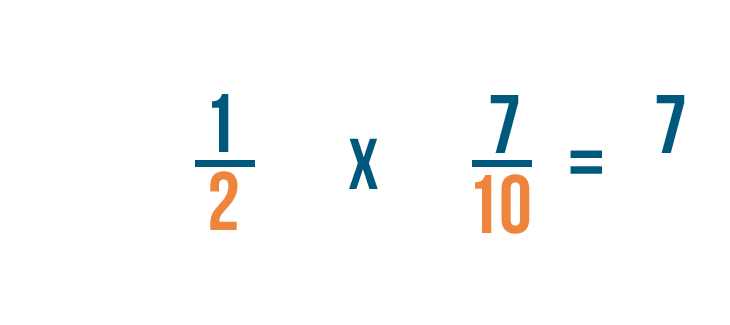
Quando abbiamo aggiunto frazioni, i denominatori sono rimasti uguali. Ma quando moltiplichiamo, anche i denominatori vengono moltiplicati.
-
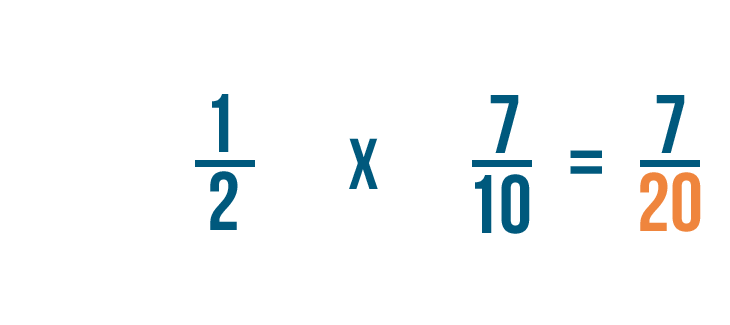
2 volte 10 è uguale a 20, quindi scriveremo 20 a destra dei denominatori.
-
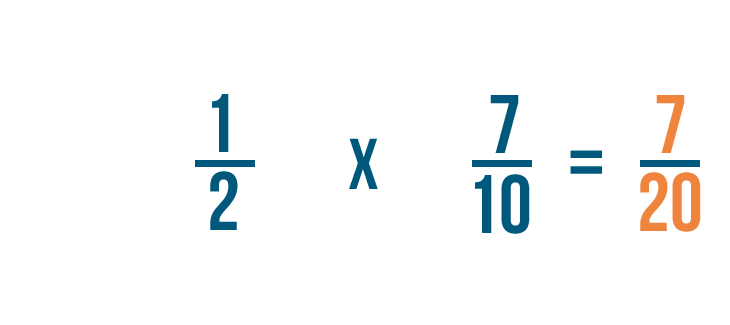
Ora sappiamo che 1/2 per 7/10 è uguale a 7/20.
-
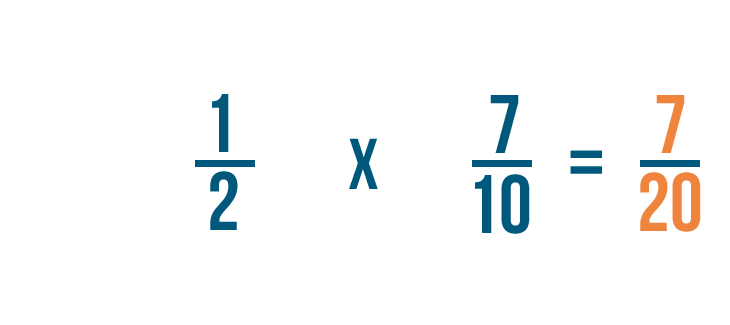
Possiamo anche dire che 1/2 di 7/10 è 7/20.
-
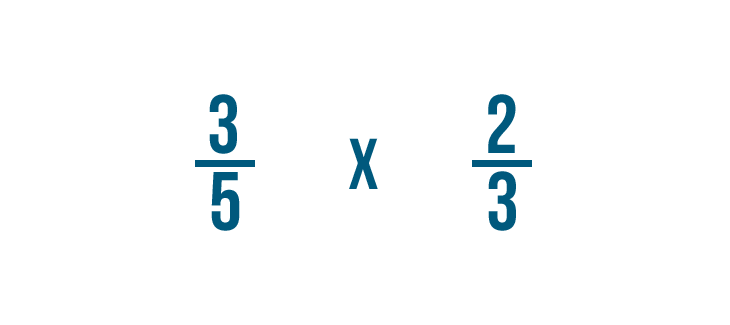
Provo un altro esempio: 3/5 per 2/3.
-
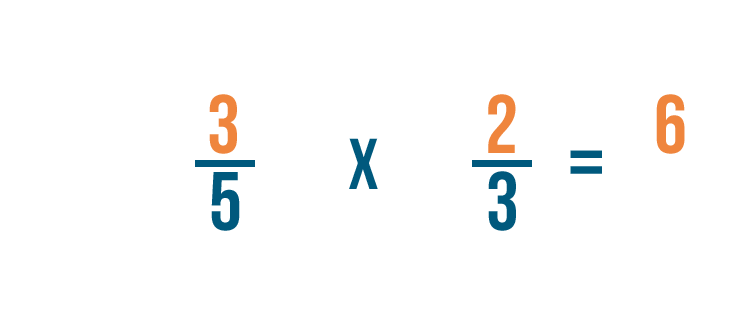
Per prima cosa, moltiplichiamo i nostri numeratori. 3 volte 2 è uguale a 6.
-
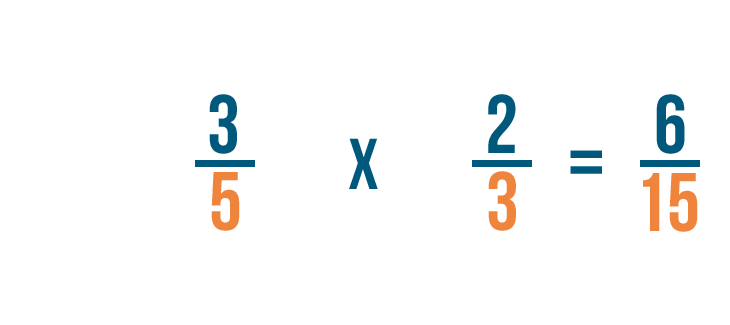
Poi moltiplichiamo i nostri denominatori. 5 volte 3 è uguale a 15.
-
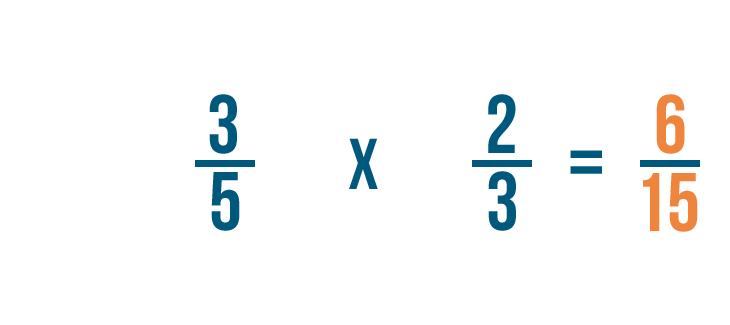
Quindi 3/5 per 2/3 è uguale a 6/15.

Try This!
Prova a risolvere i problemi di moltiplicazione qui sotto.
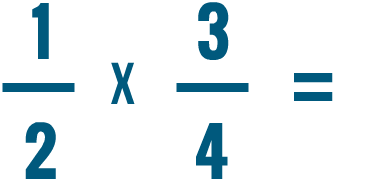
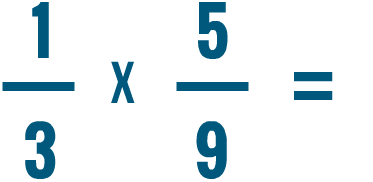
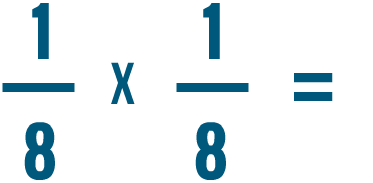
Moltiplicare una frazione e un numero intero
Moltiplicare una frazione e un numero intero è simile a moltiplicare due frazioni. C’è solo un passo in più: Prima di poter moltiplicare, dovrai trasformare il numero intero in una frazione. Questa presentazione ti mostrerà come fare.
Clicca sulla presentazione per imparare a moltiplicare una frazione e un numero intero.
-
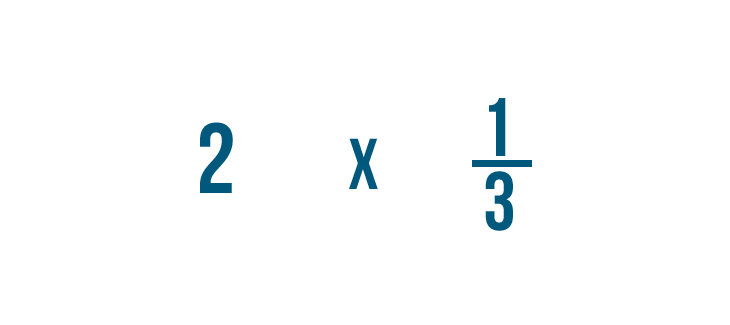
Moltiplichiamo 2 volte 1/3. Ricordate, questo è solo un altro modo di chiedere: “Cos’è 1/3 di 2?”
-
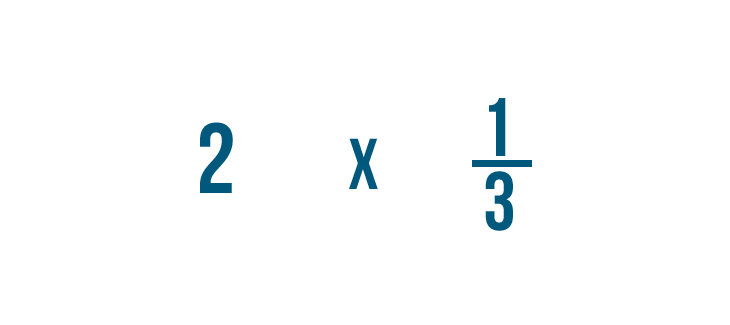
Prima di iniziare, dobbiamo assicurarci che questi numeri siano pronti per essere moltiplicati.
-
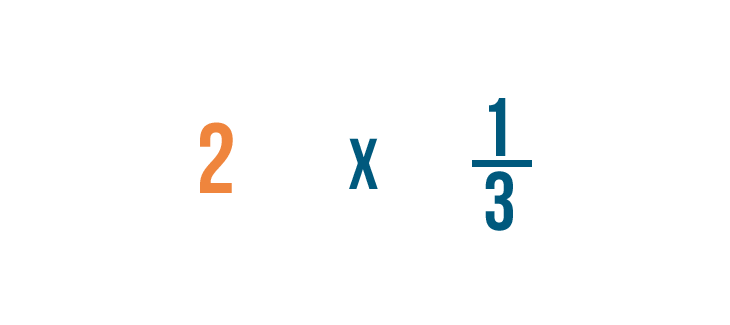
Non possiamo moltiplicare un numero intero e una frazione, quindi dobbiamo scrivere 2 come frazione.
-
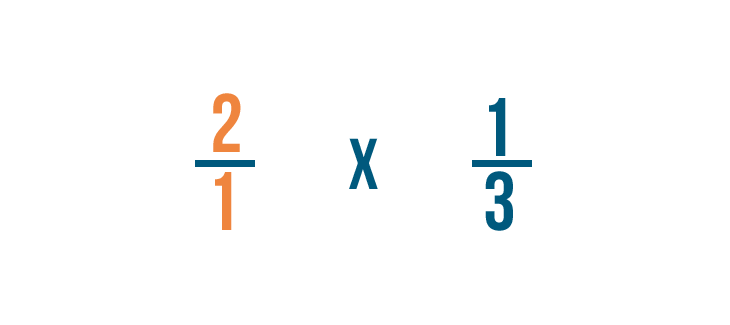
Come avete imparato in Introduzione alle Frazioni, possiamo anche scrivere 2 come 2/1. Questo perché 2 può essere diviso per 1 due volte.
-
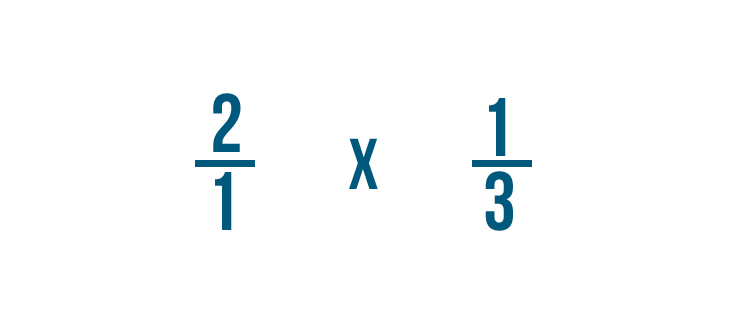
Ora siamo pronti a moltiplicare!
-
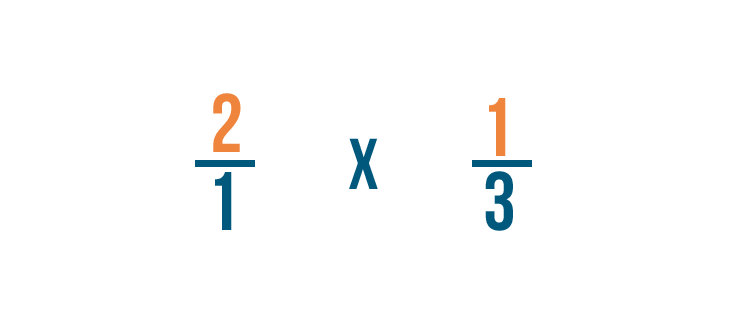
Per prima cosa, moltiplichiamo i numeratori: 2 e 1.
-
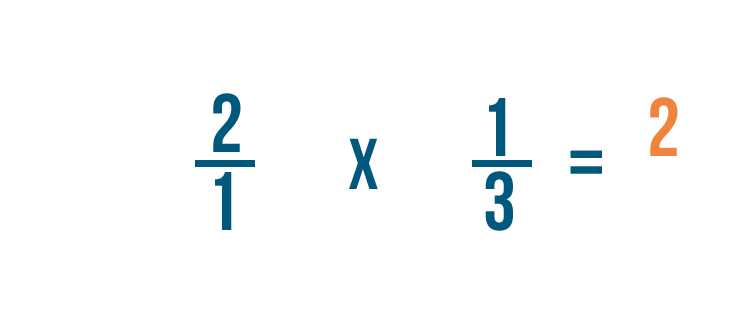
2 volte 1 è uguale a 2. Allineeremo i 2 ai numeratori.
-
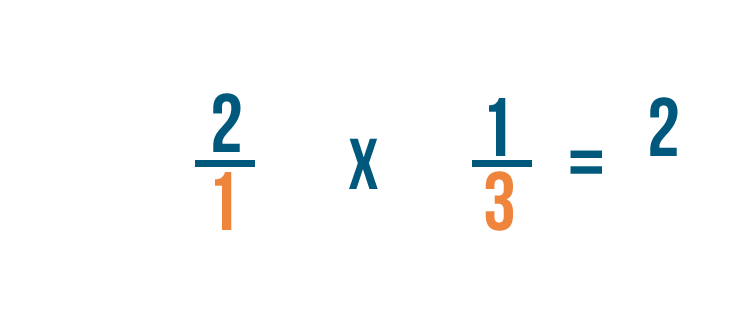
Prossimo, moltiplicheremo i denominatori: 1 e 3.
-
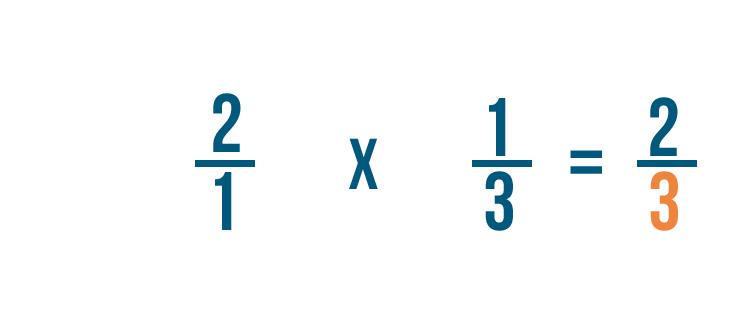
1 per 3 è uguale a 3. Allineeremo i 3 ai denominatori.
-
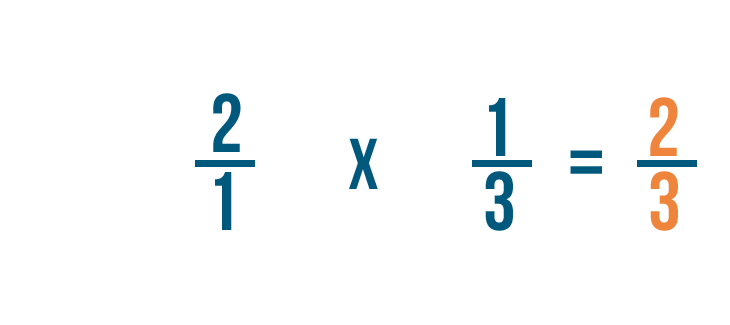
Quindi 2/1 per 1/3 è uguale a 2/3. Potremmo anche dire che 1/3 di 2 è 2/3.
-
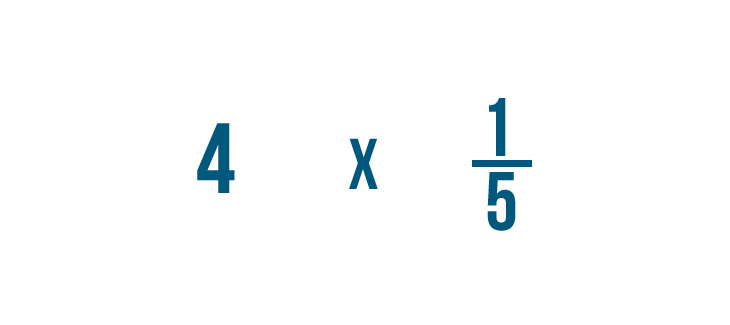
Provo un altro esempio: 4 volte 1/5.
-
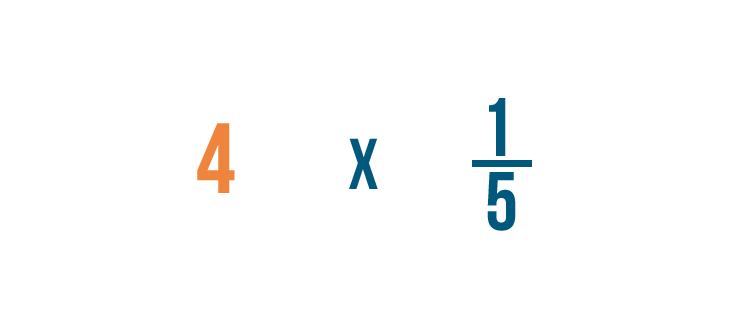
Dovremo scrivere 4 come frazione prima di iniziare.
-
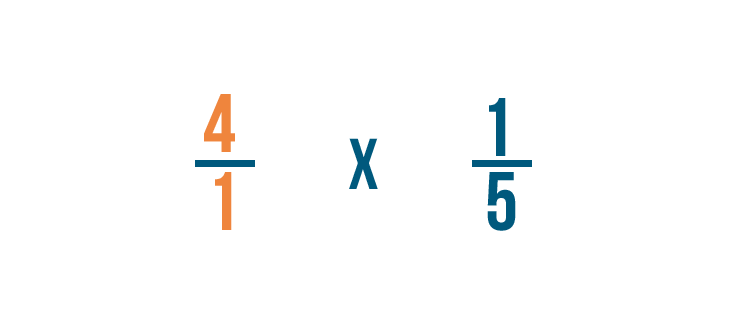
Scriveremo 4 come 4/1. Ora siamo pronti a moltiplicare.
-
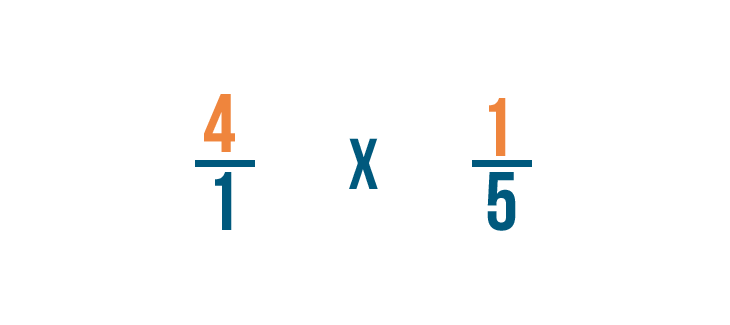
Per prima cosa, moltiplichiamo i numeratori: 4 e 1.
-
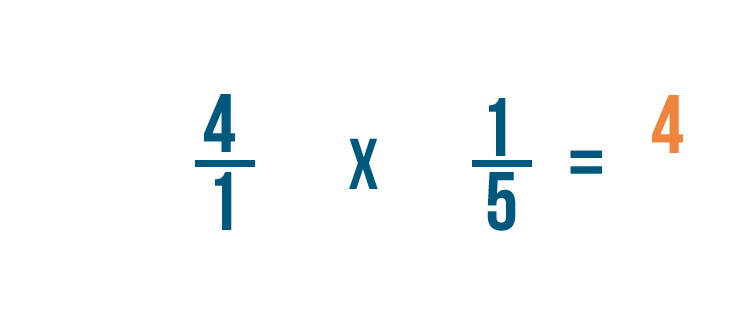
4 volte 1 è uguale a 4, quindi il numeratore della nostra risposta è 4.
-
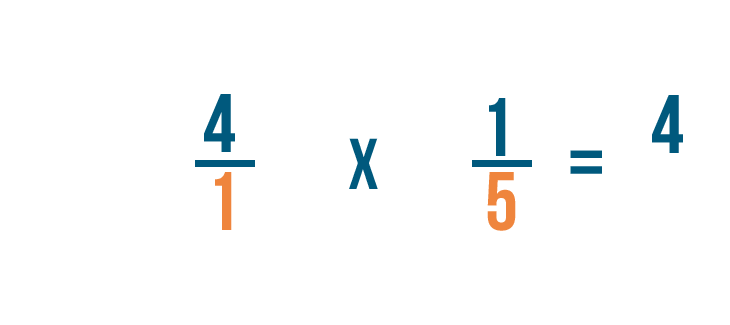
In seguito, moltiplichiamo i denominatori: 1 e 5.
-
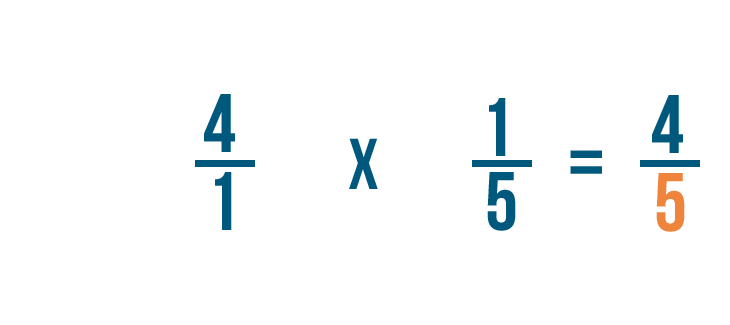
1 per 5 è uguale a 5, quindi 5 è il denominatore della nostra risposta.
-
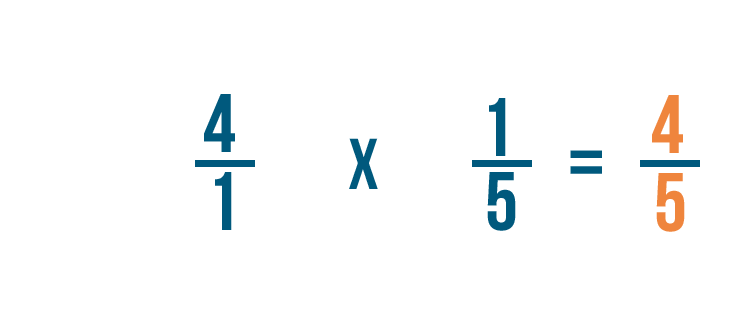
Quindi 4/1 per 1/5 è uguale a 4/5.

Prova questo!
Prova a risolvere i problemi di moltiplicazione qui sotto.
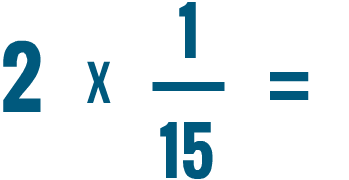
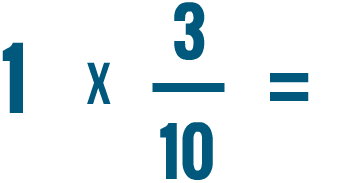
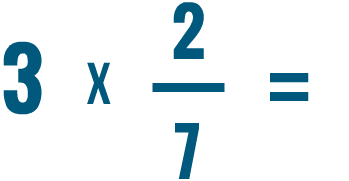
Dividere frazioni
Nelle ultime pagine, hai imparato come moltiplicare le frazioni. Potresti aver capito che puoi anche dividere le frazioni. Si dividono le frazioni per vedere quante parti di qualcosa sono in qualcos’altro. Per esempio, se vuoi sapere quanti quarti di pollice ci sono in quattro pollici, puoi dividere 4 per 1/4.
Proviamo un altro esempio. Immaginate che una ricetta richieda 3 tazze di farina, ma il vostro misurino contiene solo 1/3, o un terzo, di una tazza. Quanti terzi di tazza dovresti aggiungere?
Abbiamo bisogno di scoprire quanti terzi di tazza ci sono in tre tazze. In altre parole, dovremo dividere tre per un terzo.
Scriveremo il problema in questo modo:
3 ÷ 1/3
Prova questo!
Prova ad impostare questi problemi di divisione con le frazioni. Non preoccuparti ancora di risolverli!
Una ricetta richiede 3/4 di una tazza d’acqua. Tu hai solo un misurino da 1/8.

Risolvere i problemi di divisione con le frazioni
Ora che sappiamo come scrivere i problemi di divisione, facciamo pratica risolvendone alcuni. Dividere frazioni è molto simile alla moltiplicazione. Richiede solo un passo in più. Se sai moltiplicare le frazioni, sai anche dividerle!
Clicca sulla presentazione per imparare a dividere un numero intero per una frazione.
-
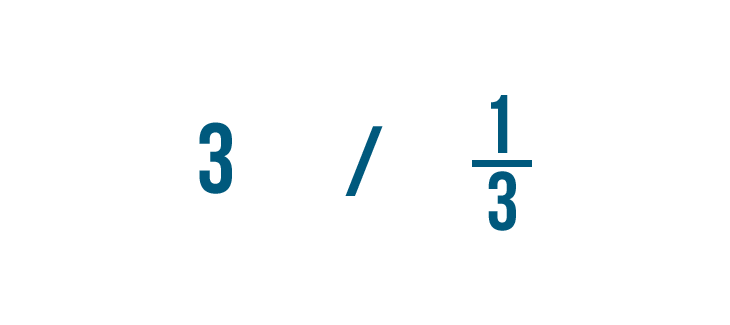
Dividiamo 3 per 1/3. Ricorda, questo è solo un altro modo di chiedere: “Quanti terzi ci sono in 3?”
-
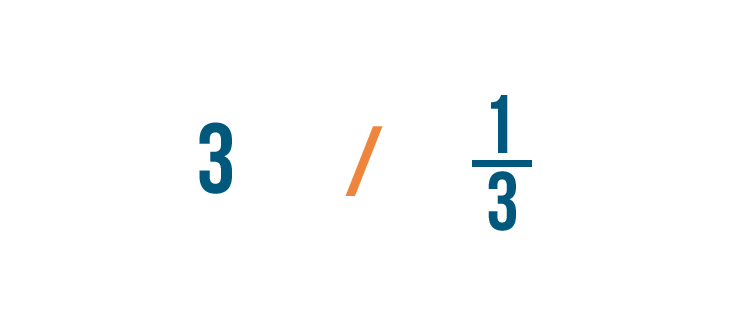
Nella nostra lezione sulla divisione, hai imparato a scrivere il segno di divisione così (/).
-
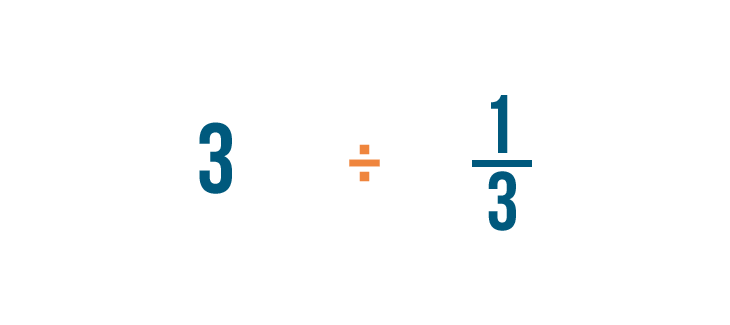
Quando si dividono frazioni, sarà utile usare l’altro simbolo per la divisione (÷) in modo da non scambiarlo per una frazione.
-
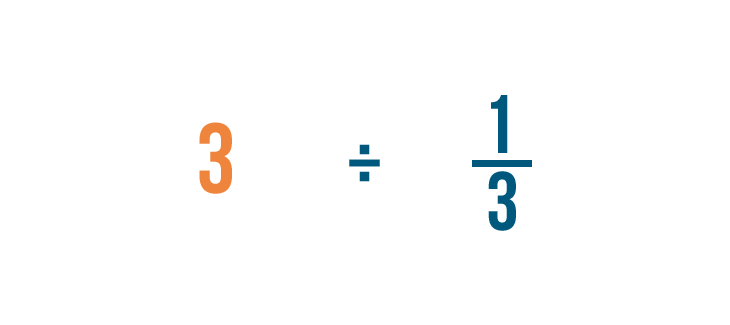
Proprio come per la moltiplicazione, inizieremo a cercare qualsiasi numero intero nel nostro problema. Ce n’è uno: 3.
-
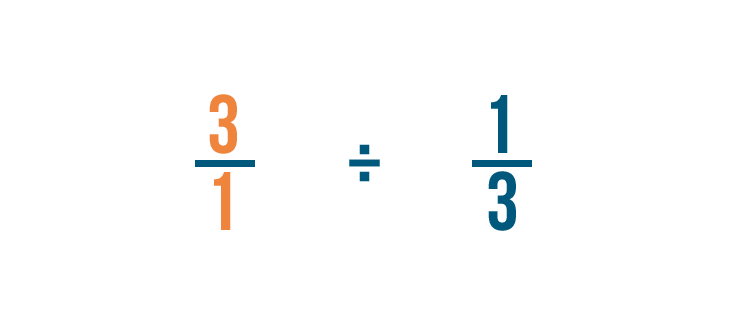
Ricordo che 3 è la stessa cosa di 3/1.
-
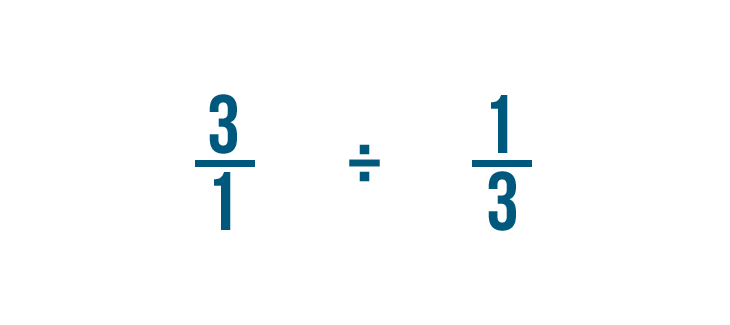
Prima di poter dividere, dobbiamo fare un altro cambiamento.
-
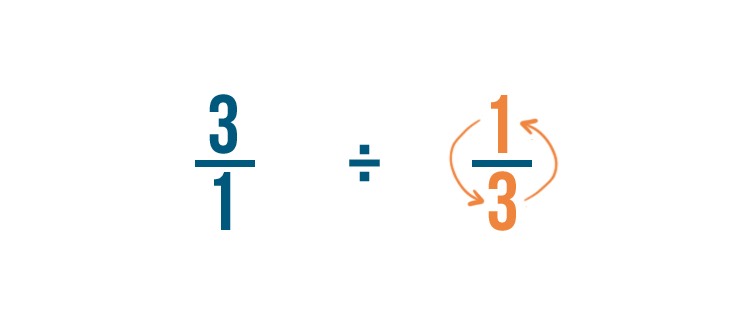
Cambieremo il numeratore e il denominatore della frazione per cui stiamo dividendo: 1/3 in questo esempio.
-
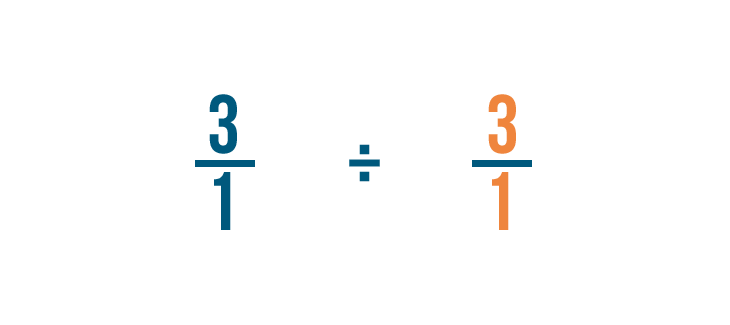
Quindi 1/3 diventa 3/1.
-
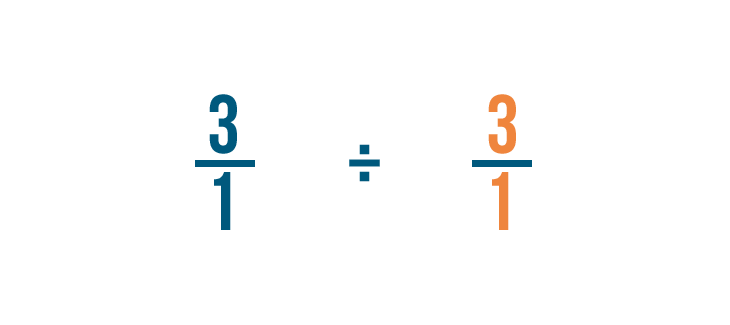
Questo si chiama trovare il reciproco, o inverso moltiplicativo, della frazione.
-
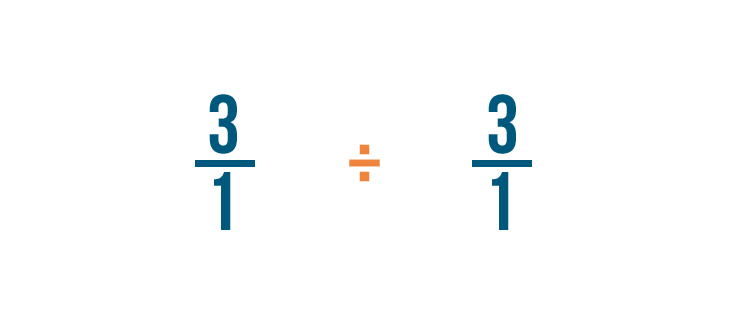
Siccome stiamo cambiando la nostra frazione originale, cambieremo anche il segno di divisione (÷) in un segno di moltiplicazione (x).
-
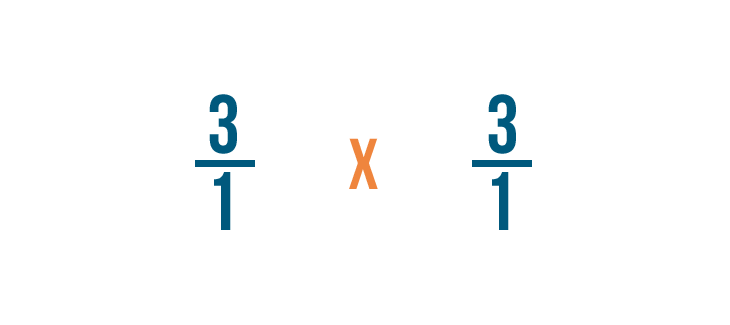
Questo perché la moltiplicazione è l’inverso della divisione.
-
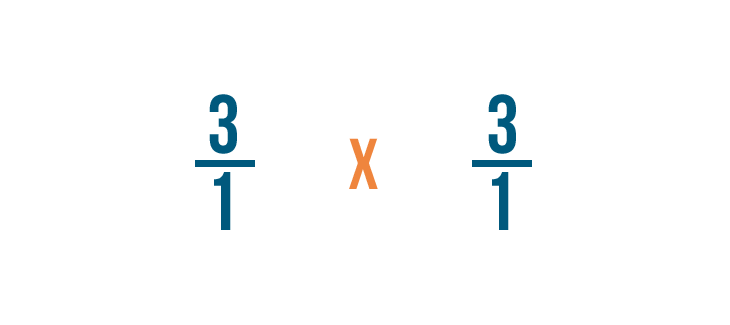
Ora possiamo trattare questo come un normale problema di moltiplicazione.
-
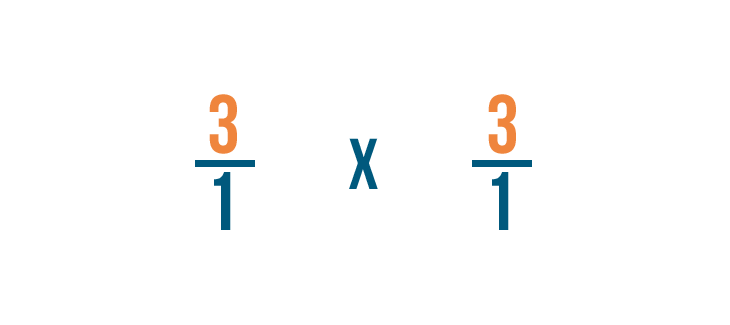
Primo, moltiplichiamo i numeratori: 3 e 3.
-
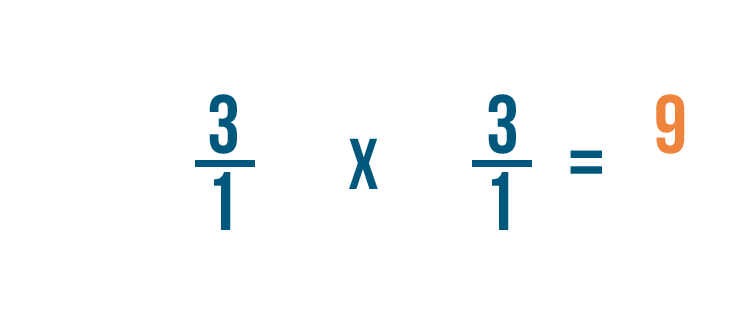
3 volte 3 è uguale a 9, quindi lo scriveremo accanto ai numeratori.
-
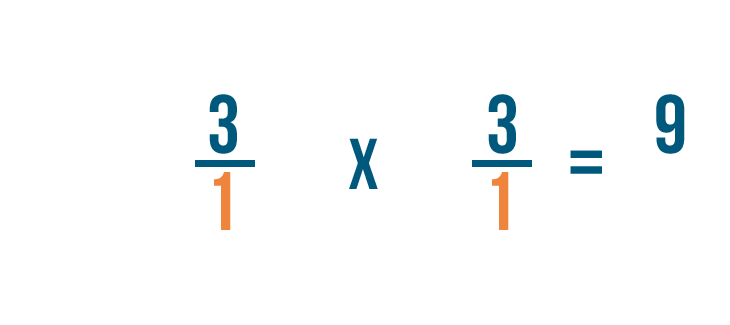
In seguito, moltiplicheremo i denominatori: 1 e 1.
-
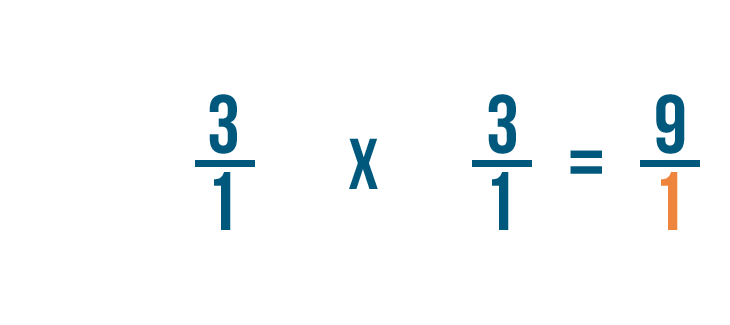
1 per 1 è uguale a 1, quindi scriveremo 1 accanto al denominatore.
-
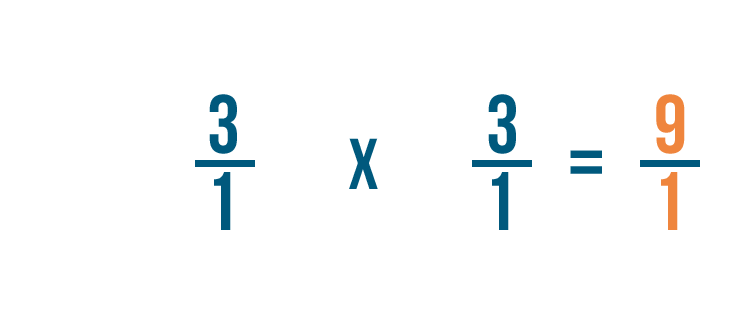
Come potete vedere, 3/1 x 1/3 = 9/1.
-
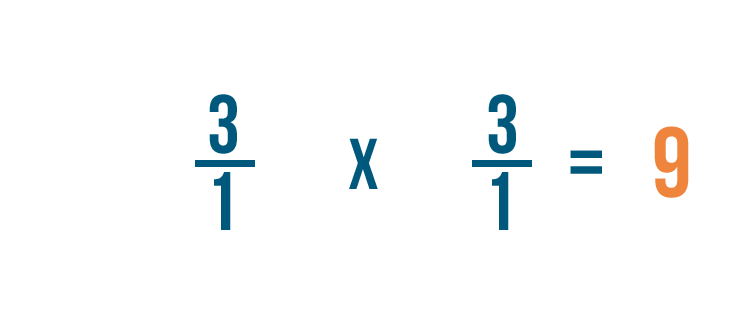
Ricordate, qualsiasi frazione superiore a 1 può essere espressa anche come numero intero. Quindi 9/1 = 9.
-
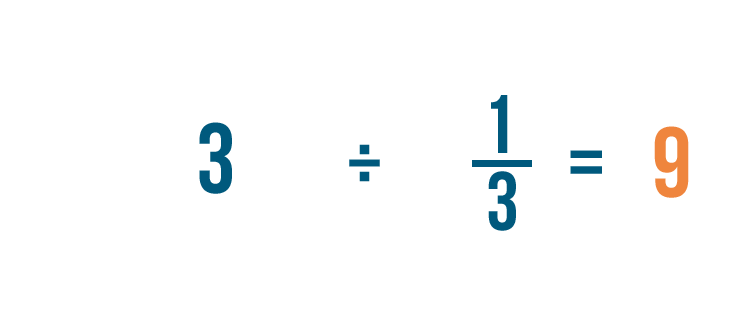
3 ÷ 1/3 = 9. In altre parole, ci sono 9 terzi in 3.
-
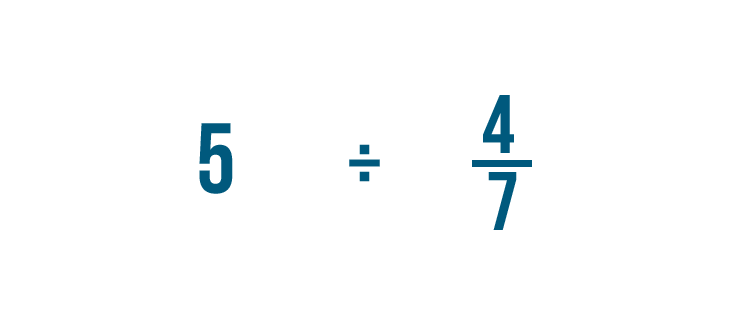
Prova un altro esempio: 5 diviso 4/7.
-
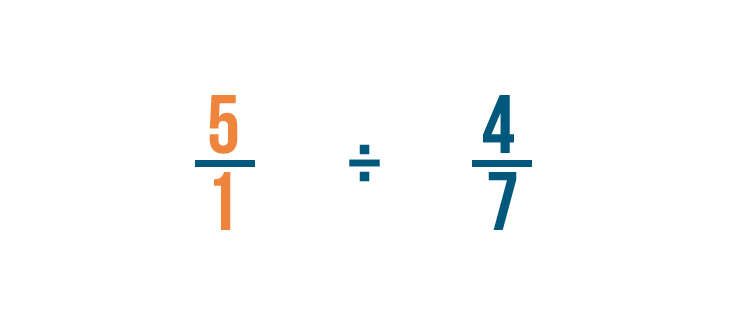
Come sempre, riscriveremo qualsiasi numero intero, quindi 5 diventa 5/1.
-
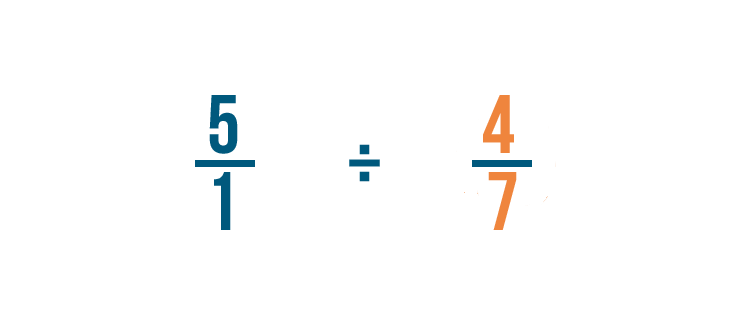
In seguito, troveremo il reciproco di 4/7. Questa è la frazione per cui stiamo dividendo.
-
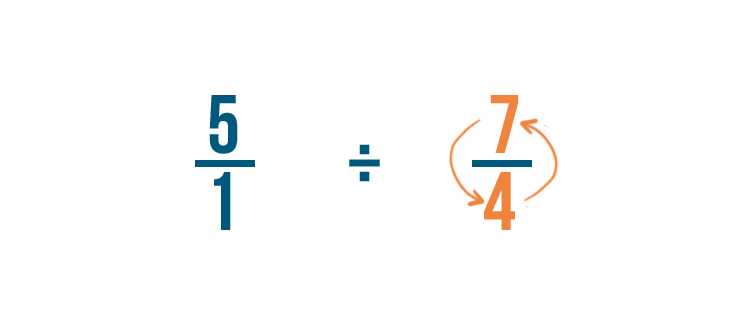
Per fare questo, scambieremo il numeratore e il denominatore, così 4/7 diventa 7/4.
-
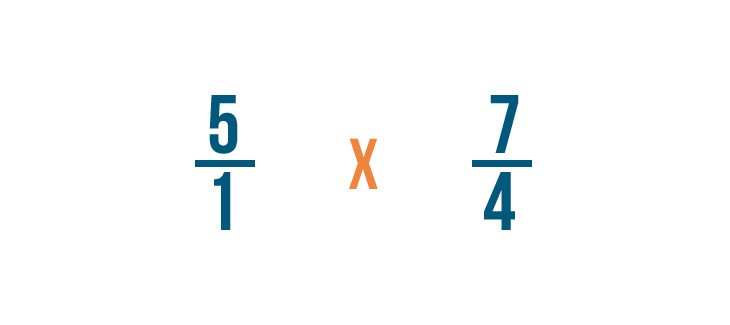
Poi cambieremo il segno di divisione (÷) in un segno di moltiplicazione (x).
-
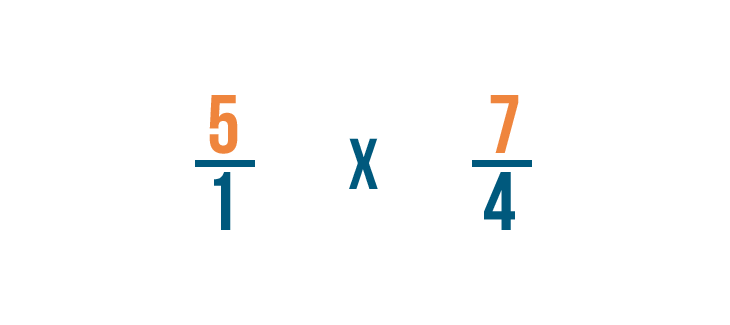
Ora possiamo moltiplicare come faremmo normalmente. Per prima cosa, moltiplichiamo i numeratori: 5 e 7.
-
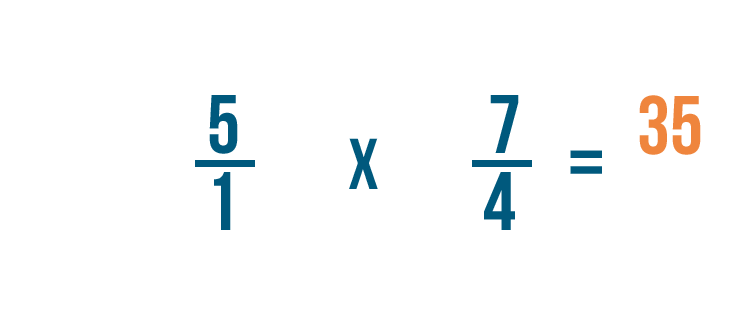
5 volte 7 è uguale a 35, quindi lo scriveremo accanto ai numeratori.
-
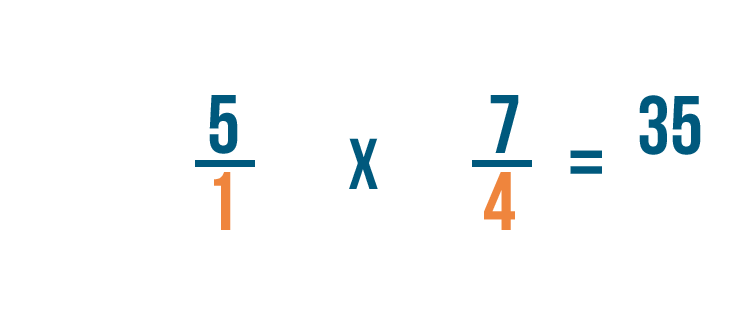
In seguito, moltiplicheremo i denominatori: 1 e 4.
-
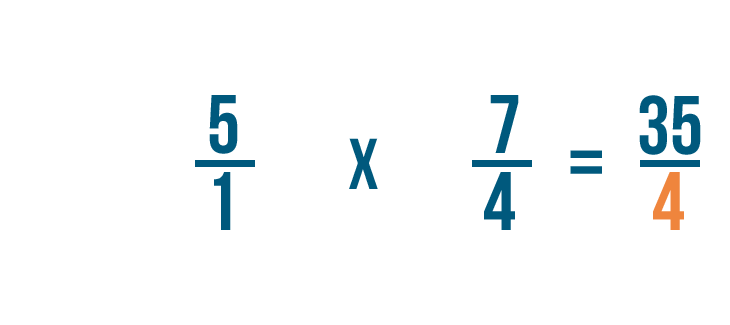
1 per 4 è uguale a 4, quindi lo scriveremo accanto ai denominatori.
-
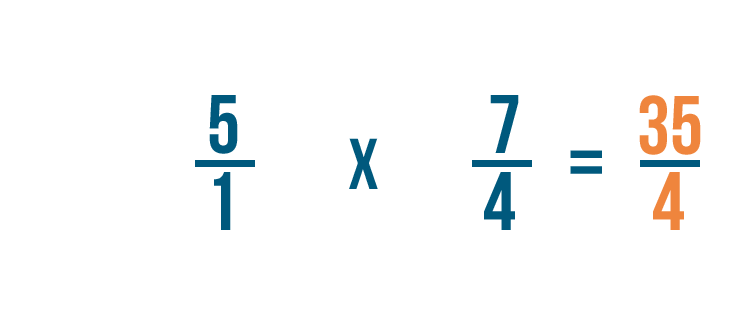
Quindi 5/1 x 4/7 = 35/4.
-
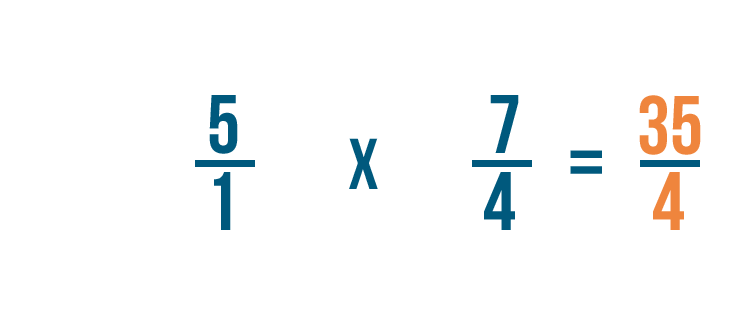
Come avete imparato prima, potremmo convertire la nostra frazione impropria in un numero misto per rendere la nostra risposta più facile da leggere.
-
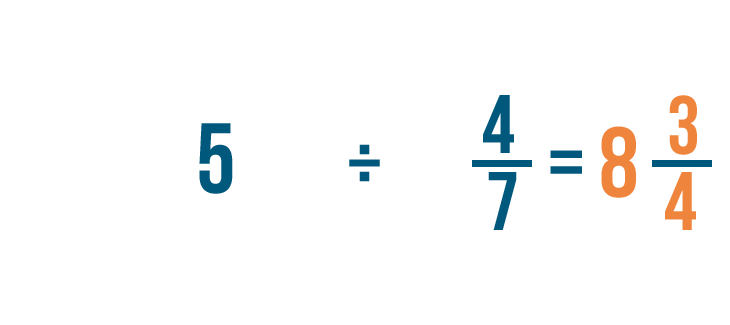
35/4 = 8 3/4. Quindi 5 ÷ 4/7 = 8 3/4.

Prova questo!
Prova a risolvere questi problemi di divisione. Non preoccuparti di ridurre la risposta per ora.
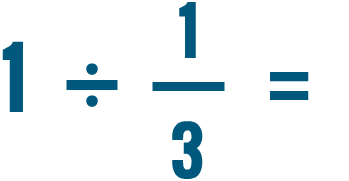
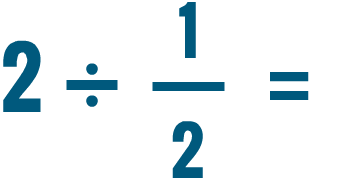
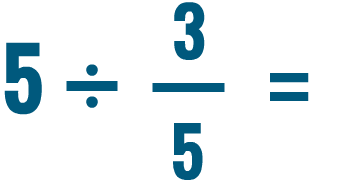
Dividere due frazioni
Abbiamo appena imparato come dividere un numero intero per una frazione. Puoi usare lo stesso metodo per dividere due frazioni.
Clicca sulla presentazione per imparare a dividere con due frazioni.
-
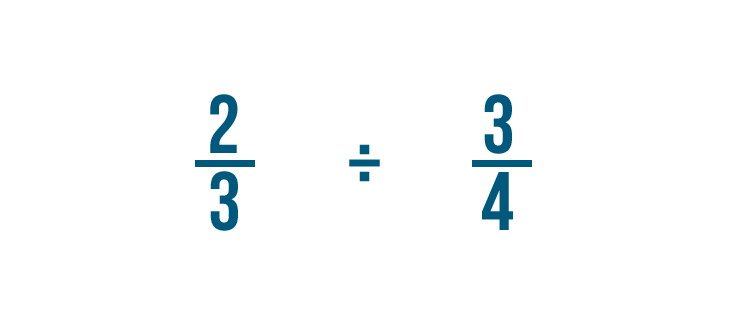
Proviamo un problema con due frazioni: 2/3 ÷ 3/4. Qui, vogliamo sapere quanti 3/4 ci sono in 2/3.
-
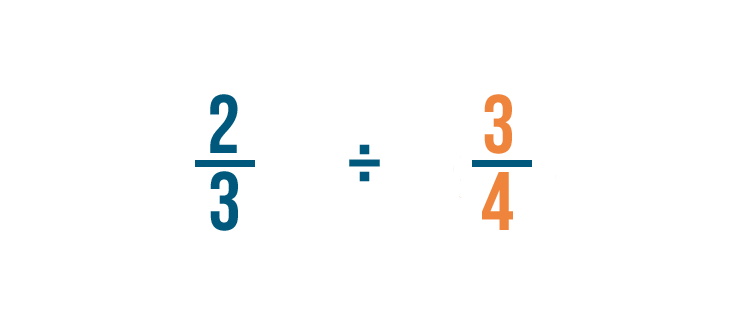
Prima, troveremo il reciproco della frazione per cui stiamo dividendo: 3/4.
-
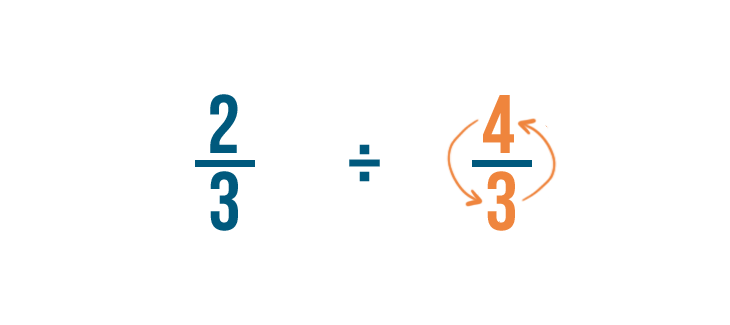
Per farlo, scambieremo il numeratore e il denominatore. Così 3/4 diventa 4/3.
-
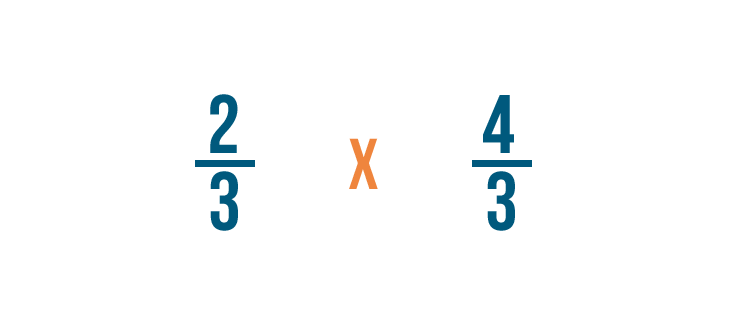
In seguito, cambieremo il segno di divisione (÷) in un segno di moltiplicazione (x).
-
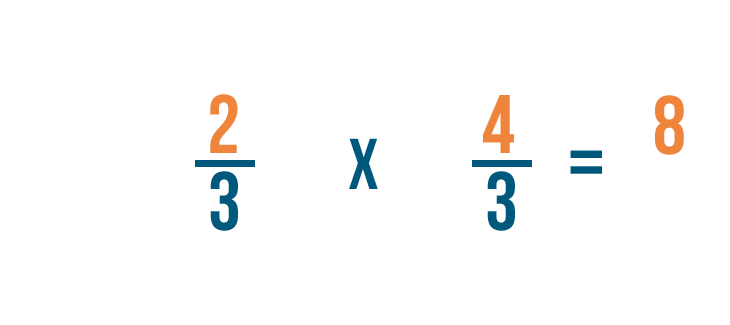
Ora moltiplichiamo i numeratori. 2 x 4 = 8, quindi scriveremo 8 accanto ai numeri superiori.
-
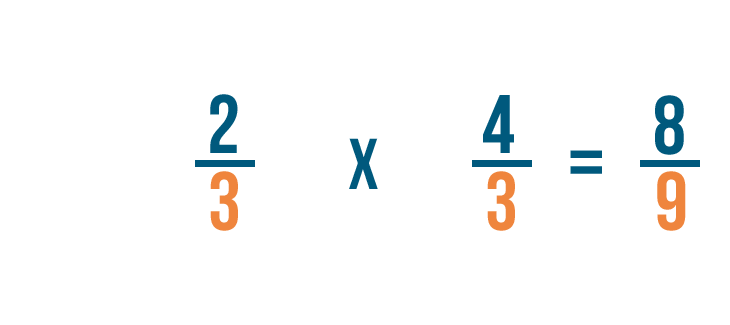
Prossimo, moltiplichiamo i denominatori. 3 x 3 = 9, quindi scriveremo 9 accanto ai numeri inferiori.
-
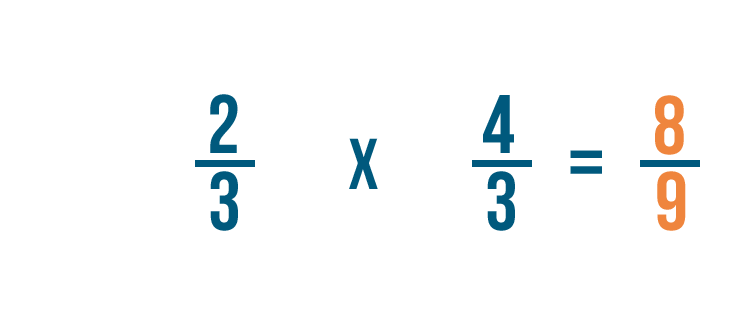
Quindi 2/3 x 4/3 = 8/9.
-
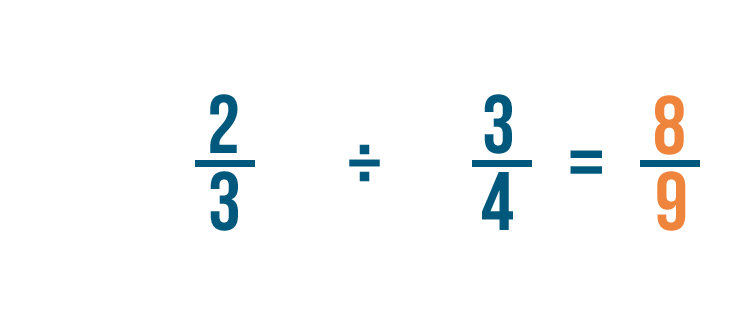
Potremmo anche scrivere questo come 2/3 ÷ 3/4 = 8/9.
-
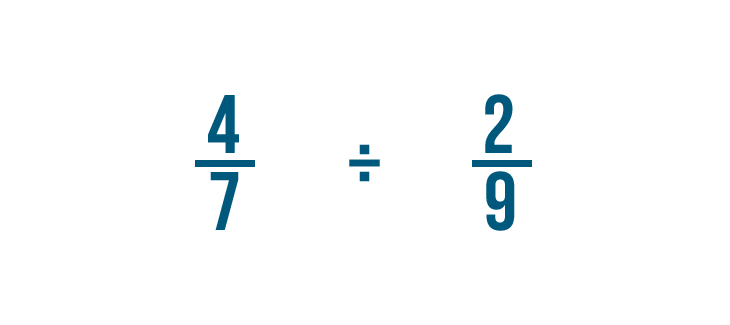
Proviamo un altro esempio: 4/7 diviso 2/9.
-
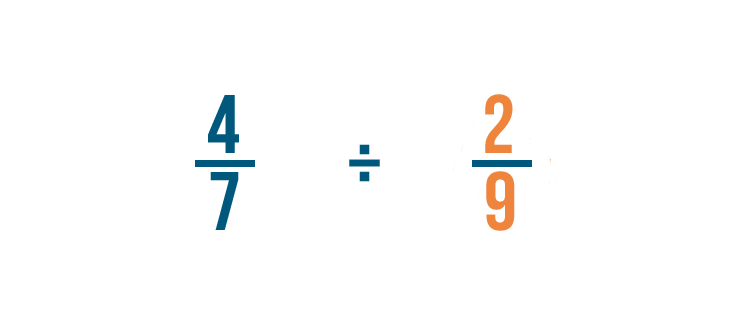
Non ci sono numeri interi, quindi troveremo il reciproco della frazione per cui stiamo dividendo. Questo è 2/9.
-
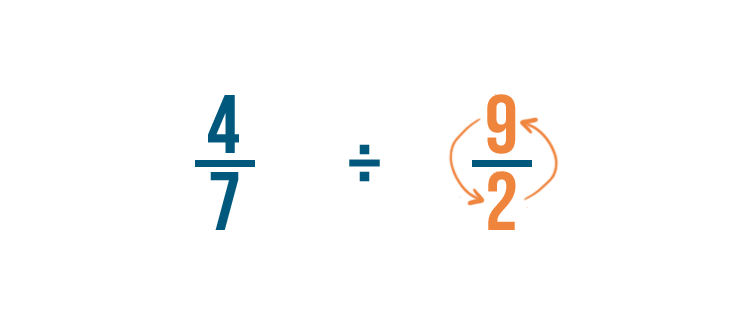
Per farlo, scambieremo il numeratore e il denominatore. Così 2/9 diventa 9/2.
-
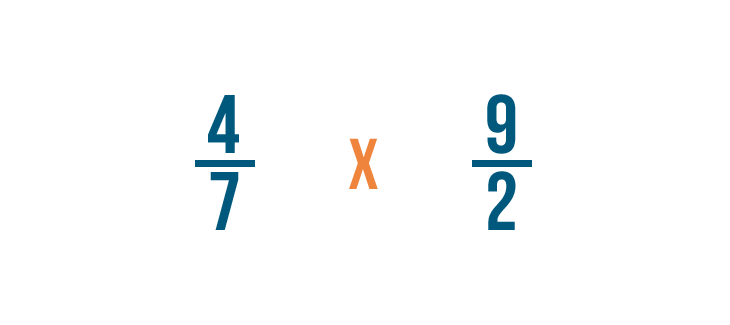
Ora cambieremo il segno di divisione (÷) in un segno di moltiplicazione (x) e moltiplicheremo normalmente.
-
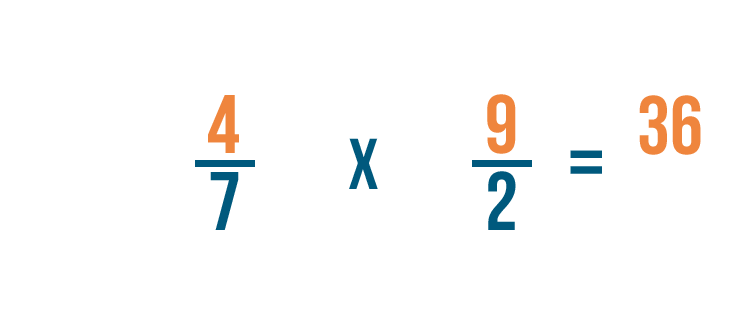
Per prima cosa, moltiplichiamo i numeratori. 4 x 9 = 36.
-
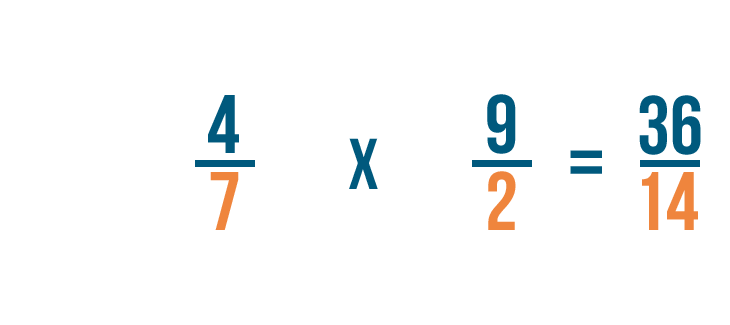
Poi moltiplichiamo i denominatori. 7 x 2 = 14.
-
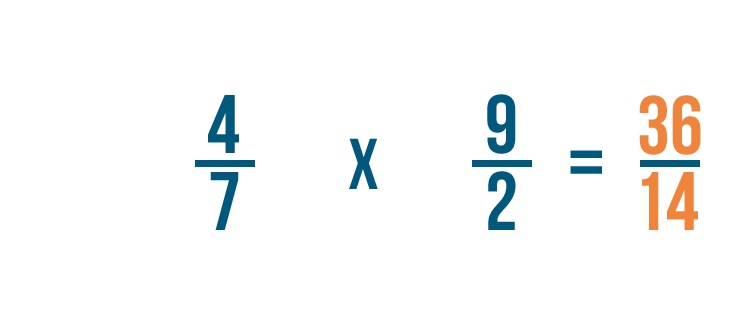
Quindi 4/7 x 9/2 = 36/14. Proprio come prima, puoi convertire questa frazione impropria in un numero misto.
-
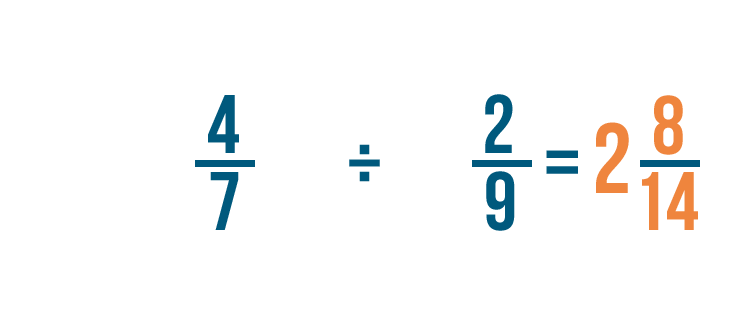
Quindi 4/7 ÷ 2/9 = 2 8/14.

Prova questo!
Prova a risolvere questi problemi di divisione. Non preoccuparti di ridurre la risposta per ora.
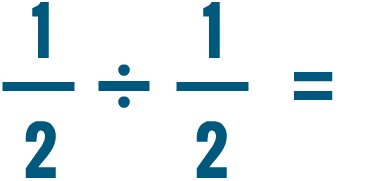
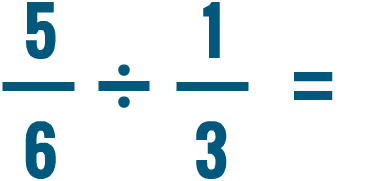
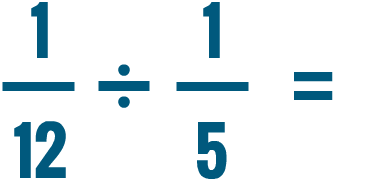
Moltiplicazione e divisione di numeri misti
Come risolveresti un problema come questo?
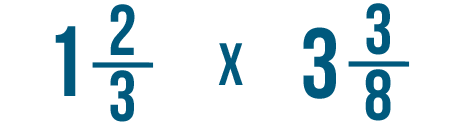
Come hai imparato nella lezione precedente, ogni volta che risolvi un problema con un numero misto devi prima convertirlo in una frazione impropria. Poi puoi moltiplicare o dividere come al solito.
Utilizzare l’annullamento per semplificare i problemi
A volte potresti dover risolvere problemi come questo:
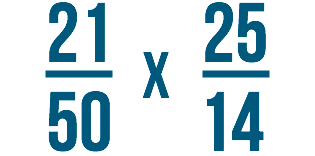
Entrambe queste frazioni includono numeri grandi. Potresti moltiplicare queste frazioni allo stesso modo di qualsiasi altra frazione. Tuttavia, numeri grandi come questo possono essere difficili da capire. Puoi immaginare 21/50, o ventuno cinquantesimi, nella tua testa?
21/50 x 25/14 = 525/700
Anche la risposta sembra complicata. È 525/700, ovvero cinquecentoventicinque settantesimi. Che boccone!
Se non ti piace lavorare con numeri grandi, puoi semplificare un problema come questo usando un metodo chiamato annullamento. Quando annulli le frazioni in un problema, le riduci entrambe allo stesso tempo.
L’annullamento può sembrare complicato all’inizio, ma ti mostreremo come farlo passo dopo passo. Diamo un’altra occhiata all’esempio che abbiamo appena visto.
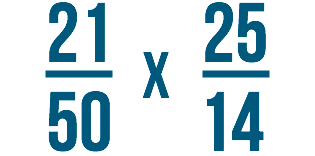
Passo 1
Primo, guarda il numeratore della prima frazione e il denominatore della seconda. Vogliamo vedere se possono essere divisi per lo stesso numero.
Nel nostro esempio, sembra che sia 21 che 14 possano essere divisi per 7.
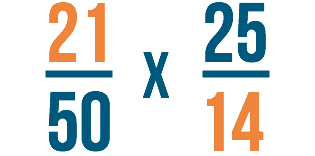
Step 2
In seguito, divideremo 21 e 14 per 7. Prima dividiamo il nostro numero in alto a sinistra: 21.
21 ÷ 7 = 3
Poi dividiamo il numero in basso a destra: 14.
14 ÷ 7 = 2
Scriviamo le risposte di ogni problema accanto ai numeri che abbiamo diviso. Poiché 21 ÷ 7 è uguale a 3, scriveremo 3 dove c’era il 21. 14 ÷ 7 è uguale a 2, quindi scriveremo 2 dove c’era il 14. Possiamo barrare, o cancellare, i numeri con cui abbiamo iniziato.
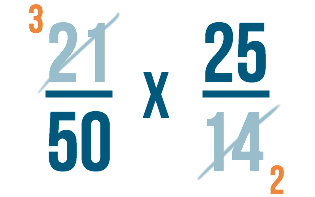
Il nostro problema sembra molto più semplice ora, vero?
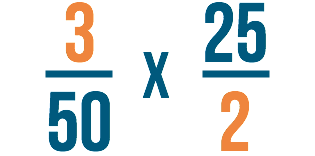
Step 3
Guardiamo gli altri numeri della frazione. Questa volta guarderemo il denominatore della prima frazione e il numeratore della seconda. Possono essere divisi per lo stesso numero?
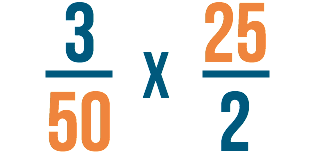
Nota che possono essere entrambi divisi per 25! Potresti anche aver notato che possono essere entrambi divisi per 5. Potremmo usare anche 5, ma generalmente quando stai annullando, vuoi cercare il numero più grande per cui entrambi i numeri possono essere divisi. In questo modo non dovrai ridurre di nuovo la frazione alla fine.
Passo 4
Prossimo, annulleremo proprio come abbiamo fatto nel passo 2.
Divideremo il nostro numero in basso a sinistra: 50.
50 ÷ 25 = 2
Poi divideremo il numero in alto a destra: 25.
25 ÷ 25 = 1
Scriveremo le risposte ad ogni problema accanto ai numeri che abbiamo diviso.
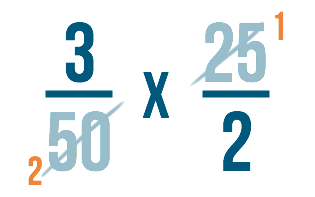
Passo 5
Ora che abbiamo annullato le frazioni originali, possiamo moltiplicare le nostre nuove frazioni come faremmo normalmente. Come sempre, moltiplica prima i numeratori:
3 x 1 = 3
Poi moltiplica i denominatori:
2 x 2 = 4
Quindi 3/2 x 1/2 =3/4, o tre quarti.
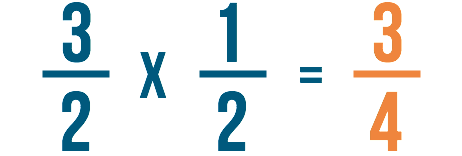
Passo 6
Finalmente, ricontrolliamo il nostro lavoro. 525/700 sarebbe stata la nostra risposta se avessimo risolto il problema senza annullare. Se dividiamo sia 525 che 700 per 175, possiamo vedere che 525/700 è uguale a 3/4.
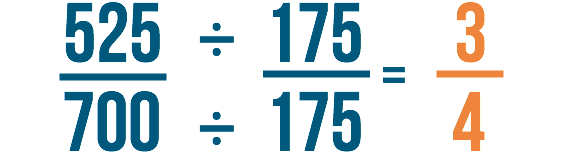
Potremmo anche dire che stiamo riducendo 525/700 a 3/4. Ricorda, l’annullamento è solo un altro modo di ridurre le frazioni prima di risolvere un problema. Otterrai la stessa risposta, non importa quando le riduci.
/it/fractions/converting-percentages-decimals-and-fractions/content/
0 commenti