
Leonhard Euler, 1707 – 1783
Cominciamo ad introdurre il protagonista di questa storia – la formula di Eulero:
Per quanto semplice possa sembrare, questa piccola formula racchiude una proprietà fondamentale di quei solidi tridimensionali che chiamiamo poliedri e che hanno affascinato i matematici per oltre 4000 anni. In realtà posso andare oltre e dire che la formula di Eulero ci dice qualcosa di molto profondo sulla forma e sullo spazio. La formula porta il nome del famoso matematico svizzero Leonhard Euler (1707 – 1783), che quest’anno avrebbe festeggiato il suo 300° compleanno.
Cos’è un poliedro?
Prima di esaminare cosa ci dice la formula di Eulero, vediamo i poliedri un po’ più in dettaglio. Un poliedro è un oggetto solido la cui superficie è composta da un certo numero di facce piane che sono delimitate da linee rette. Ogni faccia è infatti un poligono, una forma chiusa nel piano piatto bidimensionale costituita da punti uniti da linee rette.
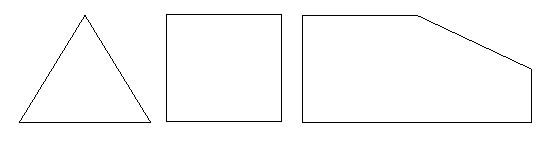
Figura 1: Il familiare triangolo e il quadrato sono entrambi poligoni, ma i poligoni possono avere anche forme più irregolari come quella mostrata sulla destra.
I poligoni non possono avere buchi, come illustra la figura sottostante: la forma a sinistra è un poligono, mentre quella a destra no.
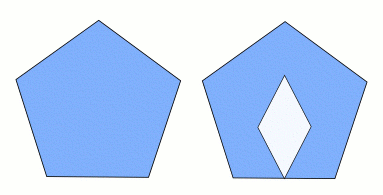
Un poligono è detto regolare se tutti i suoi lati hanno la stessa lunghezza, e tutti gli angoli tra loro sono uguali; il triangolo e il quadrato in figura 1 e il pentagono in figura 2 sono regolari.
Un poliedro è ciò che si ottiene quando si sposta una dimensione verso l’alto. È un oggetto chiuso e solido la cui superficie è composta da un certo numero di facce poligonali. Chiamiamo i lati di queste facce spigoli – due facce si incontrano lungo ognuno di questi spigoli. Chiamiamo gli angoli delle facce vertici, in modo che ogni vertice giaccia su almeno tre facce diverse. Per illustrare questo, ecco due esempi di poliedri ben noti.
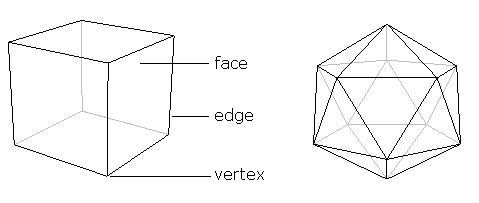
Figura 3: Il familiare cubo sulla sinistra e l’icosaedro sulla destra. Un poliedro consiste di facce poligonali, i loro lati sono conosciuti come spigoli, e gli angoli come vertici.
Un poliedro consiste di un solo pezzo. Non può, per esempio, essere composto da due (o più) parti fondamentalmente separate unite solo da uno spigolo o da un vertice. Questo significa che nessuno dei seguenti oggetti è un vero poliedro.
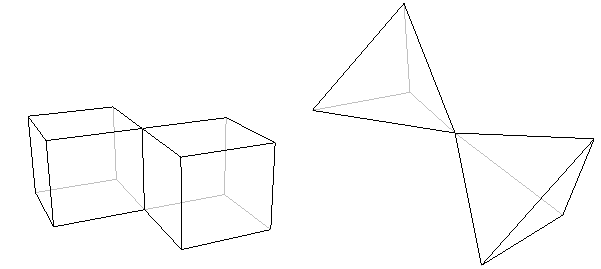
Figura 4: Questi oggetti non sono poliedri perché sono costituiti da due parti separate che si incontrano solo in uno spigolo (a sinistra) o in un vertice (a destra).
Cosa ci dice la formula?
Siamo ora pronti per vedere cosa ci dice la formula di Eulero sui poliedri. Guarda un poliedro, per esempio il cubo o l’icosaedro qui sopra, conta il numero di vertici che ha, e chiama questo numero V. Il cubo, per esempio, ha 8 vertici, quindi V = 8. Poi, conta il numero di spigoli che il poliedro ha, e chiama questo numero E. Il cubo ha 12 spigoli, quindi nel caso del cubo E = 12. Infine, conta il numero di facce e chiamalo F. Nel caso del cubo, F = 6. Ora la formula di Eulero ci dice che
o, in parole: il numero di vertici, meno il numero di spigoli, più il numero di facce, è uguale a due.
Nel caso del cubo, abbiamo già visto che V = 8, E = 12 e F = 6. Quindi,
che è quello che la formula di Eulero ci dice che dovrebbe essere. Se ora guardiamo l’icosaedro, troviamo che V = 12, E = 30 e F = 20. Ora,
La formula di Eulero è vera per il cubo e l’icosaedro. Si scopre, piuttosto meravigliosamente, che è vera praticamente per ogni poliedro. Gli unici poliedri per cui non funziona sono quelli che hanno dei buchi che li attraversano come quello mostrato nella figura qui sotto.
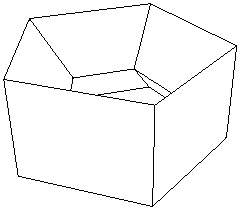
Figura 5: Questo poliedro ha un buco che lo attraversa. La formula di Eulero non vale in questo caso.
Questi poliedri sono chiamati non semplici, in contrasto con quelli che non hanno buchi, che sono chiamati semplici. I poliedri non semplici potrebbero non essere i primi a venire in mente, ma ce ne sono molti là fuori, e non si può sfuggire al fatto che la formula di Eulero non funziona per nessuno di loro. Tuttavia, anche questo fatto imbarazzante è diventato parte di una nuova teoria sullo spazio e sulla forma.
Il potere della formula di Eulero
Ogni volta che i matematici trovano una caratteristica invariante, una proprietà che è vera per un’intera classe di oggetti, sanno di aver trovato qualcosa di buono. La usano per indagare quali proprietà può avere un singolo oggetto e per identificare le proprietà che tutti devono avere. La formula di Eulero può dirci, per esempio, che non esiste un poliedro semplice con esattamente sette spigoli. Non c’è bisogno di sedersi con cartone, forbici e colla per scoprirlo – la formula è tutto ciò che serve. L’argomentazione che dimostra che non esiste un poliedro con sette spigoli è abbastanza semplice, quindi dategli un’occhiata se vi interessa.
Utilizzando la formula di Eulero in modo simile possiamo scoprire che non esiste un poliedro semplice con dieci facce e diciassette vertici. Il prisma mostrato sotto, che ha un ottagono come base, ha dieci facce, ma il numero di vertici è sedici. La piramide, che ha una base di nove lati, ha anche dieci facce, ma ha dieci vertici. Ma la formula di Eulero ci dice che nessun poliedro semplice ha esattamente dieci facce e diciassette vertici.
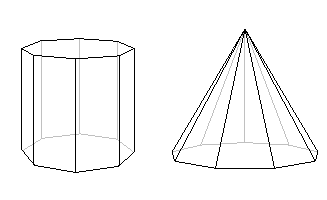
Figura 6: Entrambi questi poliedri hanno dieci facce, ma nessuno ha diciassette vertici.
Sono considerazioni come queste che ci portano alla scoperta probabilmente più bella di tutte. Si tratta dei solidi platonici, una nota classe di poliedri che prende il nome dall’antico filosofo greco Platone, nei cui scritti apparvero per la prima volta.
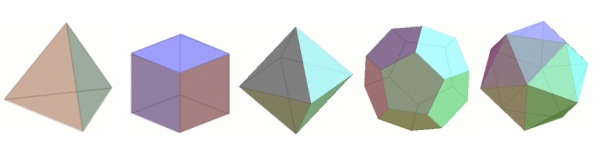
Figura 7: I solidi platonici. Da sinistra a destra abbiamo il tetraedro a quattro facce, il cubo a sei facce, l’ottaedro a otto facce, il dodecaedro a dodici facce e l’icosaedro a venti facce. Si scopre che è descritta da due caratteristiche. La prima è che i solidi platonici non hanno picchi o avvallamenti, quindi la loro forma è bella e rotonda. In altre parole, questo significa che ogni volta che si scelgono due punti in un solido platonico e si traccia una linea retta tra loro, questo pezzo di linea retta sarà completamente contenuto all’interno del solido – un solido platonico è quello che si chiama convesso. La seconda caratteristica, chiamata regolarità, è che tutte le facce del solido sono poligoni regolari con esattamente lo stesso numero di lati, e che lo stesso numero di spigoli esce da ogni vertice del solido.
Il cubo è regolare, poiché tutte le sue facce sono quadrati e da ogni vertice escono esattamente tre spigoli. Puoi verificare da solo che anche il tetraedro, l’ottaedro, l’icosaedro e il dodecaedro sono regolari. Fin dalla scoperta del cubo e del tetraedro, i matematici furono così attratti dall’eleganza e dalla simmetria dei solidi platonici che ne cercarono altri, e tentarono di elencarli tutti. È qui che entra in gioco la formula di Eulero. Puoi usarla per trovare tutte le possibilità per il numero di facce, spigoli e vertici di un poliedro regolare e scoprirai che ci sono solo cinque diversi poliedri convessi regolari! Questo è molto sorprendente; dopo tutto, non c’è limite al numero di diversi poligoni regolari, quindi perché dovremmo aspettarci un limite qui? I cinque solidi platonici sono il tetraedro, il cubo, l’ottaedro, l’icosaedro e il dodecaedro mostrato sopra.
La dimostrazione

René Descartes,
(1596 – 1650)
Giocare con vari poliedri semplici vi mostrerà che la formula di Eulero è sempre vera. Ma se sei un matematico, questo non basta. Volete una prova, un argomento logico a prova di bomba che vi mostri che funziona davvero per tutti i poliedri, compresi quelli che non avrete mai il tempo di controllare.

Adrien-Marie Legendre, (1752 – 1833)
A dispetto del nome della formula, non è stato Eulero a proporre la prima dimostrazione completa. La sua storia è complessa, abbraccia 200 anni e coinvolge alcuni dei più grandi nomi della matematica, tra cui René Descartes (1596 – 1650), Euler stesso, Adrien-Marie Legendre (1752 – 1833) e Augustin-Louis Cauchy (1789 – 1857).

Augustin-Louis Cauchy, (1789 – 1857)
È interessante notare che tutti questi matematici hanno usato approcci molto diversi per dimostrare la formula, ognuno dei quali colpisce per la sua ingegnosità e intuizione. È la dimostrazione di Cauchy, però, che vorrei darvi un assaggio qui. Il suo metodo consiste in diverse fasi e passi. La prima fase comporta la costruzione di quella che viene chiamata una rete.
Formazione di una rete
Immagina di avere in mano il tuo poliedro con una faccia rivolta verso l’alto. Ora immaginate di “rimuovere” solo questa faccia, lasciando i bordi e i vertici intorno ad essa, in modo da avere una “scatola” aperta. Poi immaginate di potervi aggrappare alla scatola e tirare i bordi della faccia mancante l’uno dall’altro. Se li tiri abbastanza lontano, la scatola si appiattirà e diventerà una rete di punti e linee nel piano. La serie di diagrammi qui sotto illustra questo processo applicato ad un cubo.
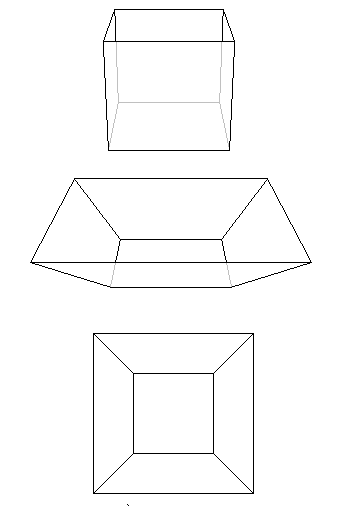
Figura 8: Trasformare il cubo in una rete.
Come potete vedere dal diagramma qui sopra, ogni faccia del poliedro diventa un’area della rete circondata da bordi, e questo è ciò che chiameremo una faccia della rete. Queste sono le facce interne della rete. C’è anche una faccia esterna che consiste nell’area esterna alla rete; questa corrisponde alla faccia che abbiamo rimosso dal poliedro. Quindi la rete ha vertici, spigoli dritti e facce poligonali.
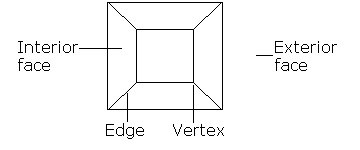
Figura 9: La rete ha facce, spigoli e vertici.
Quando hai formato la rete non hai aggiunto né rimosso alcun vertice, quindi la rete ha lo stesso numero di vertici del poliedro – V. La rete ha anche lo stesso numero di spigoli – E – del poliedro. Ora per le facce; tutte le facce del poliedro, tranne quella “mancante”, appaiono “dentro” la rete. La faccia mancante è diventata la faccia esterna che si estende tutto intorno alla rete. Così, compresa la faccia esterna, la rete ha F facce. Così, si può usare la rete, piuttosto che il poliedro stesso, per trovare il valore di V – E + F. Andremo ora a trasformare la nostra rete per rendere questo valore più facile da calcolare.
Trasformare la rete
Ci sono tre tipi di operazioni che possiamo eseguire sulla nostra rete. Introdurremo tre passi che li coinvolgono.
Passo 1 Iniziamo guardando le facce poligonali della rete e chiediamo: c’è una faccia con più di tre lati? Se c’è, disegniamo una diagonale come mostrato nel diagramma qui sotto, dividendo la faccia in due facce più piccole.
Figura 10: Dividere le facce.
Ripetiamo questa operazione con la nostra faccia scelta fino a quando la faccia è stata suddivisa in triangoli.
Figura 11: Alla fine ci ritroviamo con delle facce triangolari.
Se c’è un’altra faccia con più di tre lati, usiamo il passo 1 su quella faccia finché anche questa è stata suddivisa in facce triangolari. In questo modo, possiamo scomporre ogni faccia in facce triangolari, e otteniamo una nuova rete, le cui facce sono tutte triangolari. Illustriamo questo processo mostrando come trasformeremmo la rete che abbiamo creato da un cubo.
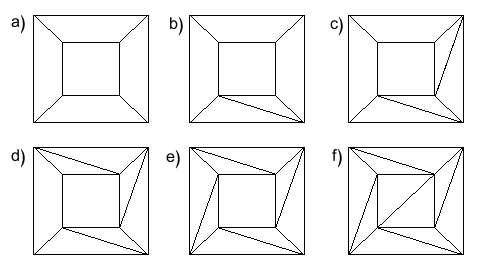
Figura 12: Questo è ciò che accade alla rete del cubo quando eseguiamo ripetutamente il passo 1.
Torniamo al passo 1, e guardiamo la rete che otteniamo dopo aver eseguito il passo 1 solo una volta. Ora, disegnando una diagonale abbiamo aggiunto uno spigolo. La nostra faccia originale è diventata due facce, quindi abbiamo aggiunto una al numero di facce. Non abbiamo cambiato il numero di vertici. La rete ora ha V vertici, E + 1 bordi e F + 1 facce. Quindi come è cambiato V – E + F dopo che abbiamo eseguito il passo 1 una volta? Usando quello che sappiamo sui cambiamenti in V, E e F possiamo vedere che V – E + F è diventato V – (E + 1) + (F + 1). Ora abbiamo
Quindi V – E + F non è cambiato dopo il passo 1! Poiché ogni utilizzo del passo 1 lascia V – E + F invariato, è ancora invariato quando raggiungiamo la nostra nuova rete composta interamente da triangoli! L’effetto su V – E + F quando trasformiamo la rete fatta dal cubo è mostrato nella tabella qui sotto.
| Round | V | E | F | V – E + F | |
| (a) | 8 | 12 | 6 | 2 | |
| (b) | 8 | 13 | 7 | 2 | |
| (c) | 8 | 14 | 8 | 2 | |
| (d) | 8 | 15 | 9 | 2 | |
| (e) | 8 | 16 | 10 | 2 | |
| (f) | 8 | 17 | 11 | 2 |
Introduciamo ora i passi 2 e 3. Essi rimuoveranno le facce dall’esterno della rete, riducendo il numero di facce passo dopo passo. Una volta che cominciamo a fare questo, la rete probabilmente non rappresenterà più un poliedro, ma la proprietà importante della rete è mantenuta.
Step 2 Controlliamo se la rete ha una faccia che condivide solo un bordo con la faccia esterna. Se ce l’ha, rimuoviamo questa faccia rimuovendo l’unico bordo condiviso. L’area che era stata coperta dalla faccia scelta diventa parte della faccia esterna, e la rete ha un nuovo confine. Questo è illustrato dal diagramma qui sotto per la rete fatta dal cubo.
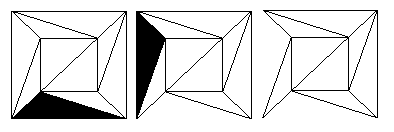
Figura 13: Rimozione di facce con un bordo esterno.
Ora, prenderemo V, E e F come i numeri di vertici, bordi e facce che la rete fatta di facce triangolari aveva prima di eseguire il passo 2. Ora guardiamo come il numero V – E + F è cambiato dopo aver eseguito il passo 2 una volta. Abbiamo rimosso un bordo, quindi la nostra nuova rete ha E – 1 bordi. Non abbiamo toccato affatto i vertici, quindi abbiamo ancora V vertici. La faccia che abbiamo usato per il passo 2 è stata fusa con la faccia esterna, quindi ora abbiamo F – 1 facce. Quindi V – E + F è diventato V – (E – 1) + (F – 1) e
Quindi ancora una volta V – E + F non è cambiato.
Step 3 Controlliamo se la nostra rete ha una faccia che condivide due bordi con la faccia esterna. Se è così, rimuoviamo questa faccia rimuovendo sia questi bordi condivisi che il loro vertice condiviso, in modo che ancora una volta l’area appartenente alla faccia scelta diventi parte della faccia esterna. Questo è illustrato qui sotto nel caso della rete fatta dal cubo, come è dopo aver eseguito il passo 2 due volte.
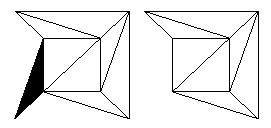
Figura 14: Rimozione delle facce con due bordi esterni.
Come abbiamo fatto prima, ora prendiamo V, E e F come numeri di vertici, bordi e facce della rete da cui stiamo partendo. Ora come è stato influenzato il numero V – E + F dal passo 3? Abbiamo rimosso un vertice – quello tra i due bordi – quindi ora ci sono V – 1 vertici. Abbiamo rimosso due bordi, quindi ora ci sono E – 2 bordi. Infine, la nostra faccia scelta si è fusa con la faccia esterna, così ora abbiamo F – 1 facce. Così V – E + F è diventato (V – 1) – (E – 2) – (F – 1) e
Così ancora una volta V – E + F non è cambiato.
Il segreto della prova sta nell’eseguire una sequenza dei passi 2 e 3 per ottenere una rete molto semplice. Ricordiamo che abbiamo usato ripetutamente il passo 1 per produrre una rete con solo facce triangolari. Questa rete avrà sicuramente una faccia che condivide esattamente un bordo con la faccia esterna, quindi prendiamo questa faccia ed eseguiamo il passo 2. Possiamo eseguire il passo 2 su diverse facce, una alla volta, finché non appare una faccia che condivide due bordi con la faccia esterna. Possiamo quindi eseguire il passo 3 usando questa faccia. Continuiamo ad eseguire i passi 2 e 3, e continuiamo a rimuovere facce in questo modo.
Ci sono due regole importanti da seguire quando si fa questo. In primo luogo, dobbiamo sempre eseguire il passo 3 quando è possibile farlo; se c’è una scelta tra il passo 2 e il passo 3 dobbiamo sempre scegliere il passo 3. Se non lo facciamo, la rete potrebbe rompersi in pezzi separati. In secondo luogo, dobbiamo rimuovere le facce solo una alla volta. Se non lo facciamo, potremmo ritrovarci con dei bordi che spuntano da soli nella faccia esterna, e non avremo più una rete adeguata. Per illustrare il processo, eseguiremo diversi passi sulla rete del cubo, continuando da dove abbiamo lasciato nell’ultimo diagramma.
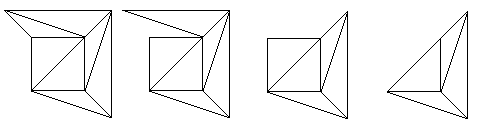
Figura 15: Applicazione del nostro algoritmo alla rete del cubo.
Ora possiamo farci una o due domande. Questo processo di rimozione delle facce si ferma mai e, se lo fa, cosa ci rimane? Una piccola considerazione vi mostrerà che deve fermarsi – ci sono solo un numero finito di facce e spigoli che possiamo rimuovere – e che quando lo fa, rimaniamo con un singolo triangolo. Puoi vedere alcuni diagrammi che descrivono l’intero processo per la rete formata da un dodecaedro (ricorda che questo era uno dei solidi platonici introdotti prima).
Ora guarda i numeri di vertici, spigoli e facce presenti nella nostra rete finale – il singolo triangolo. Abbiamo V=3, E=3, e F=2 – dobbiamo ancora includere la faccia esterna. Ora
In tutto il processo, partendo dal poliedro completo e finendo con un triangolo, il valore di V – E + F non è cambiato. Quindi se V – E + F = 2 per la rete finale, dobbiamo avere anche V – E + F = 2 per il poliedro stesso! La dimostrazione è completa!
Oltre i poliedri
Finirò accennando ad alcune conseguenze della formula di Eulero oltre il mondo dei poliedri. Inizierò con qualcosa di molto piccolo: i chip dei computer. I chip dei computer sono circuiti integrati, costituiti da milioni di minuscoli componenti collegati da milioni di piste conduttrici. Questi ricordano le nostre reti di cui sopra, tranne che di solito non è possibile disporli su un piano senza che alcune delle piste conduttrici – i bordi – si attraversino. Gli incroci sono una brutta cosa nella progettazione dei circuiti, quindi il loro numero dovrebbe essere mantenuto basso, ma trovare una disposizione adatta non è un compito facile. La formula del poliedro di Eulero, con le sue informazioni sulle reti, è un ingrediente essenziale per trovare soluzioni.
Ora passiamo al molto grande: il nostro universo. A tutt’oggi i cosmologi non sono d’accordo sulla sua forma esatta. Il perno della loro considerazione è la topologia, lo studio matematico della forma e dello spazio. Nel XIX secolo i matematici scoprirono che tutte le superfici nello spazio tridimensionale sono essenzialmente caratterizzate dal numero di buchi che hanno: i nostri semplici poliedri non hanno buchi, una ciambella ha un buco, ecc. La formula di Eulero non funziona per i poliedri con buchi, ma i matematici hanno scoperto un’eccitante generalizzazione. Per qualsiasi poliedro, V – E + F è esattamente 2 meno 2 volte il numero di buchi! Si scopre che questo numero, chiamato caratteristica di Eulero, è cruciale per lo studio di tutte le superfici tridimensionali, non solo dei poliedri. La formula di Eulero può essere vista come il catalizzatore di un modo completamente nuovo di pensare alla forma e allo spazio.
Informazioni sull’autore

Abi è cresciuta nel nord dell’Inghilterra, e si è trasferita a sud per studiare matematica all’Imperial College di Londra e alla Queen Mary, University of London. Ora insegna matematica alla Open University. Il principale interesse matematico di Abi è la teoria dei gruppi. Si è divertita molto ad esplorare i misteri della formula di Eulero mentre scriveva questo articolo.
Originariamente pubblicato il 1 giugno 2007
0 commenti