=================================================================================
Nella teoria classica della diffrazione, la diffrazione di Bragg si verifica quando particelle cariche o onde di radiazione elettromagnetica con una lunghezza d’onda comparabile alla spaziatura atomica sono incidenti su un campione cristallino. Le onde riflesse da centri di diffusione adiacenti devono avere una differenza di percorso pari a un numero integrale di lunghezze d’onda. Le onde disperse interferiscono costruttivamente se rimangono in fase. Pertanto, la differenza di percorso tra le onde elettroniche riflesse dai piani superiore e inferiore nella figura 3882 è uguale alla lunghezza totale (AO+BO). Supponendo che i piani hkl siano distanziati di una distanza dhkl e che l’onda sia incidente e riflessa con angoli θB, sia AB che BC sono uguali a dsin(θB) e la differenza di percorso totale dovrebbe essere uguale a 2dsin(θB).
Come discusso a pagina2678, possiamo avere,
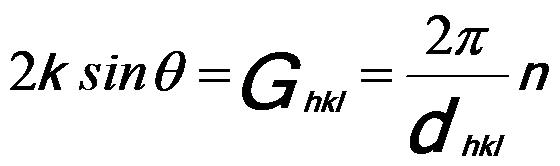 ——————————————
——————————————
dove,
n — Il multiplo intero del più piccolo Ghkl che è permesso,
k = 2π/λ.
Pertanto, possiamo ottenere la ben nota condizione di diffrazione di Bragg, data da,
nλ = 2dhklsin(θB) ——————————————–
dove,
n — Un intero, l’ordine di riflessione;
dhkl — La spaziatura reticolare di (hkl);
λ — La lunghezza d’onda della particella carica o delle onde di radiazione elettromagnetica;
θB — L’angolo di Bragg che è l’angolo tra il vettore dell’onda incidente e i piani del reticolo come mostrato nella figura 3882,
hkl — Indici di Miller.
L’angolo di Bragg θB è un concetto molto importante nella teoria della diffrazione, ad esempio ampiamente usato per spiegare i fenomeni di diffrazione di elettroni e raggi X. Intensità molto forti note come picchi di Bragg si ottengono nel modello di diffrazione quando le onde diffuse soddisfano la condizione di Bragg. L’angolo tra le onde incidenti e quelle riflesse è uguale a 2θB come mostrato nella Figura 3882.
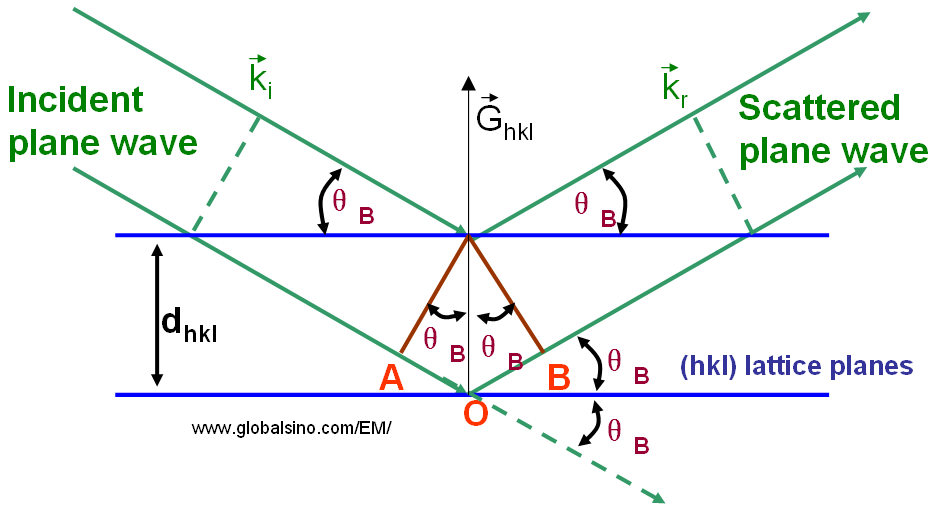
La differenza di percorso tra le onde riflesse è uguale a AO + BO.
Per le strutture FCC e BCC, le costanti di reticolo sono date da, (Puoi scaricare il file excel per i tuoi calcoli)
—————–
La tabella 3882a mostra che gli elettroni interagiscono con 1 elettrone, molti elettroni, 1 nucleo e molti nuclei nei solidi.
| Interazione con elettrone(i) | Interazione con nucleo/nuclei | |||||
|---|---|---|---|---|---|---|
| 1 elettrone | Molti elettroni | 1 nucleo | Molti nuclei | |||
| Tipo di diffusione | Inelastica | Inelastica | Quasi-elastico | Elastico | Inelastico | |
| Effetto di diffusione | Effetto Compton dell’elettrone; eccitazione di elettroni (da 50 eV a pochi keV: EDS e EELS) | Eccitazione plasmonica (< 50 eV, ~100 nm campione TEM); effetto Cerenkov | scattering Rutherford; scattering di foni (< 1 eV, calore) | scattering di Bragg | Bremsstrahlung | |
La tabella 3882b elenca alcuni esempi di angoli di Bragg a vari voltaggi di fascio per una tipica spaziatura d. Gli angoli di Bragg sono stati ottenuti con l’equazione 3882b (per n = 1).
Tabella 3882b. Angoli di Bragg a varie tensioni di fascio per una tipica spaziatura d.
| Tensione di accelerazione (kV) | Lunghezza d’onda (nm) | Cristalli | d-spaziatura (nm) | Angolo di Bragg (° & mrad) |
| 100 | 0.0037 | Cristalli biologici tipici | 10 | 0,0106° (0,19 mrad) |
| 200 | 0,0025 | Nickel (Ni) | 0,203 | 0.353° (6,16 mrad) |
Negli esperimenti attuali, a differenza della diffusione diffusa, i picchi di Bragg provengono dalla struttura ordinata a lungo raggio. I campioni cristallini devono essere inclinati in un goniometro nel TEM per:
i) Osservare le frange del reticolo e le strutture cristalline.
ii) Determinare l’orientamento del cristallo.
iii) Osservare il contrasto di diffrazione dei difetti del reticolo con determinate riflessioni di Bragg o con orientamento noto.
iv) Determinare il vettore Burgers dei difetti del reticolo.
Tabella 3882c. Script di micrografia digitale per calcolare gli angoli di riflessione dei cristalli.
| Struttura del cristallo | Scripts |
| FCC | Diffrazione elettronica, XRD |
| BCC | Diffrazione degli elettroni, XRD |
0 commenti