A volte, ci sono più di un modo per risolvere un problema. Dobbiamo imparare a confrontare le prestazioni di diversi algoritmi e scegliere il migliore per risolvere un particolare problema. Mentre analizziamo un algoritmo, consideriamo soprattutto la complessità temporale e la complessità spaziale. La complessità temporale di un algoritmo quantifica la quantità di tempo impiegato da un algoritmo per funzionare in funzione della lunghezza dell’input. Allo stesso modo, la complessità spaziale di un algoritmo quantifica la quantità di spazio o di memoria che un algoritmo impiega per funzionare in funzione della lunghezza dell’input.
La complessità temporale e spaziale dipende da molte cose come l’hardware, il sistema operativo, i processori, ecc. Tuttavia, non consideriamo nessuno di questi fattori mentre analizziamo l’algoritmo. Considereremo solo il tempo di esecuzione di un algoritmo.
Iniziamo con un semplice esempio. Supponiamo di avere un array $A$ e un intero $x$ e di dover trovare se $x$ esiste nell’array $A$.
Semplice soluzione a questo problema è attraversare l’intero array $A$ e controllare se un qualsiasi elemento è uguale a $x$.
for i : 1 to length of A if A is equal to x return TRUEreturn FALSEOgni operazione nel computer richiede un tempo approssimativamente costante. Che ogni operazione richieda $c$$ tempo. Il numero di linee di codice eseguite dipende effettivamente dal valore di $x$. Durante l’analisi dell’algoritmo, per lo più considereremo il caso peggiore, cioè quando $x$ non è presente nell’array $A$. Nel caso peggiore, la condizione if verrà eseguita $N$ volte dove $N$ è la lunghezza dell’array $A$. Quindi, nel caso peggiore, il tempo totale di esecuzione sarà $(N * c + c)$. $N * c$ per la condizione if e $c$ per la dichiarazione di ritorno (ignorando alcune operazioni come l’assegnazione di $i$).
Come possiamo vedere il tempo totale dipende dalla lunghezza dell’array $A$. Se la lunghezza dell’array aumenta, aumenta anche il tempo di esecuzione.
L’ordine di crescita è come il tempo di esecuzione dipende dalla lunghezza dell’input. Nell’esempio precedente, possiamo vedere chiaramente che il tempo di esecuzione dipende linearmente dalla lunghezza dell’array. L’ordine di crescita ci aiuterà a calcolare il tempo di esecuzione con facilità. Ignoreremo i termini di ordine inferiore, poiché i termini di ordine inferiore sono relativamente insignificanti per input di grandi dimensioni. Usiamo una notazione diversa per descrivere il comportamento limitante di una funzione.
$$-notation:
Per denotare il limite superiore asintotico, usiamo $$$-notation. Per una data funzione $g(n)$, denotiamo con $O(g(n))$ (pronunciato “big-oh di g di n”) l’insieme delle funzioni:
$O(g(n)) =$ { $f(n)$ : esistono costanti positive $c$ e $n_0$ tali che $0 \le f (n) \le c * g(n)$ per tutti $n \ge n_0$ }
$Omega$-notazione:
Per denotare il limite inferiore asintotico, usiamo $Omega$-notazione. Per una data funzione $g(n)$, denotiamo con $Omega(g(n))$ (pronunciato “big-omega di g di n”) l’insieme delle funzioni:
$$Omega(g(n)) =$ { $f(n)$ : esistono costanti positive $c$ e $n_0$ tali che $0 \le c * g(n) \le f(n)$ per tutti $n \ge n_0$ }
$Theta$-notation:
Per denotare un limite stretto asintotico, usiamo $Theta$-notation. Per una data funzione $g(n)$, denotiamo con $Theta(g(n))$ (pronunciato “big-theta di g di n”) l’insieme delle funzioni:
$Theta(g(n)) =$ { $f (n)$ : esistono costanti positive $c_1,\;c_2$ e $n_0$ tali che $0 \le c_1 * g(n) \le f (n) \le c_2 * g(n)$ per tutti $n \gt n_0$$ }
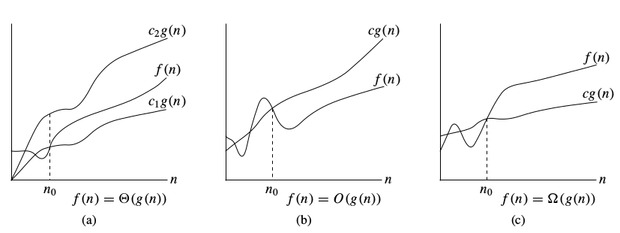
Notazioni sulla complessità temporale
Quando si analizza un algoritmo, consideriamo per lo più la notazione $O$ perché ci darà un limite superiore del tempo di esecuzione, cioè il tempo di esecuzione nel peggiore dei casi.Cioè il tempo di esecuzione nel caso peggiore.
Per calcolare la $O$-notazione ignoreremo i termini di ordine inferiore, poiché i termini di ordine inferiore sono relativamente insignificanti per input di grandi dimensioni.
Lasciamo che $f(N) = 2 * N^2 + 3 * N + 5$
$O(f(N)) = O(2 * N^2 + 3 * N + 5) = O(N^2)$
Consideriamo qualche esempio:
int count = 0;for (int i = 0; i < N; i++) for (int j = 0; j < i; j++) count++;Vediamo quante volte viene eseguito count++.
Quando $i = 0$, verrà eseguito $0$ volte.
Quando $i = 1$$, verrà eseguito $1$ volte.
Quando $i = 2$$, verrà eseguito $2$$ volte e così via.
Il numero totale di volte che count++ verrà eseguito è $0 + 1 + 2 + … + (N-1) = \frac{N * (N-1)}{2}$. Quindi la complessità temporale sarà $O(N^2)$.
int count = 0;for (int i = N; i > 0; i /= 2) for (int j = 0; j < i; j++) count++;Questo è un caso difficile. A prima vista, sembra che la complessità sia $O(N * logN)$. $N$ per il ciclo $j$ e $logN$ per il ciclo $i$. Vediamo perché.
Pensate a quante volte count++ verrà eseguito.
Quando $i = N$$, verrà eseguito $N$ volte.
Quando $i = N / 2$, verrà eseguito $N / 2$$ volte.
Quando $i = N / 4$, verrà eseguito $N / 4$ volte e così via.
Il numero totale di volte che count++ verrà eseguito è $N + N / 2 + N / 4 + … + 1 = 2 * N$. Quindi la complessità temporale sarà $O(N)$.
La tabella qui sotto è per aiutarvi a capire la crescita di diverse complessità temporali comuni, e quindi aiutarvi a giudicare se il vostro algoritmo è abbastanza veloce da ottenere un Accettato (assumendo che l’algoritmo sia corretto).
| Lunghezza dell’input (N) | Peggiore accettato Algoritmo |
|---|---|
| $$le $ | $O(N!), O(N^6)$ |
| $\le $ | $O(2^N * N^2)$ |
| $\le $ | $$ $td> $O(2^N * N)$ |
| $le 100$ | $O(N^4)$ |
| $le 400$ | $O(N^3)$ |
| $le 2K$ | $O(N^2 * logN)$ |
| $le 10K$ | $O(N^2)$ |
| $le 1M$ | $O(N * logN)$ |
| $le 100M$ | $O(N), O(logN), O(1)$ |
Passa al prossimo tutorial
0 commenti