Come controllare la quadratura, angoli a 90 gradi

Utilizzando la regola del 3 4 5 per costruire la forma a L & Pareti quadrate, stanze, tetti e altro ancora!

• Perché è necessario controllare la quadratura quando si costruiscono le cose (principalmente per risparmiarsi un sacco di dolore in seguito.)
• Come squadrare un telaio/tetto/stanza/edificio a quattro lati
• Squadrare due lati con la regola del 3 4 5 (pythagoras theorum)
• Tipi di squadre per carpentieri (strumenti) disponibili

Perché è così importante costruire cose perfettamente squadrate?

Costruire cose come muri, pavimenti o decking perfettamente vere, a piombo e quadrate è quando possibile essenziale. Vi aiuterà ad evitare problemi e a risparmiare un sacco di tempo in seguito ed è anche il modo più forte per formare praticamente delle strutture.

A volte, come per esempio nelle vecchie case, bisogna fare delle eccezioni. A volte bisogna ‘dividere la differenza’, o accettare il male minore e fare quello che si può. In questi casi immagino sempre cosa farei se si trattasse della mia casa o che sia la meno evidente/più piacevole per l’occhio.

<p>Costruire i muri quadrati garantirà che i materiali in lastre come il cartongesso siano veloci e facili da installare. Le piastre dei muri devono essere quadrate e livellate per far funzionare le travi del tetto. I ponti del giardino e i travetti del pavimento costruiti perfettamente quadrati saranno molto più facili da posare su pavimenti e rivestimenti. La lista continua, ma 10 minuti in più per controllare che tutto sia quadrato nelle fasi iniziali potrebbero farvi risparmiare ore o addirittura giorni più tardi.

Non riuscire a costruire le cose a livello e in modo corretto porterà solo a mal di testa e lavoro extra in seguito. Le porte si apriranno o chiuderanno da sole se non si installano i rivestimenti delle porte in modo piano e regolare. Le smussature saranno una bastardata da fare bene, e dovranno essere eseguite più tracciature, il che significa lavoro extra, mal di testa – e tempo/costo.

Sebbene ci siano molte squadre di carpenteria disponibili per controllare i 90°, quando si costruisce un grande muro di borchie o un ponte da giardino, per esempio, queste sono di solito troppo piccole per assicurare accuratamente che la struttura abbia angoli perfetti a 90°.

Ci sono due metodi semplici e facili da ricordare che uso.

Come controllare la quadratura di un telaio a quattro lati

Per formare un telaio quadrato o rettangolare, entrambe le piastre (superiore e inferiore) dovrebbero essere della stessa lunghezza, e tutte le borchie o i travetti dovrebbero essere della stessa lunghezza anche tra loro. Una volta inchiodata, per verificare che la struttura sia quadrata, basta misurare da un angolo all’altro.

Se le misure non sono uguali, tirare l’angolo lungo verso il centro della struttura fino a che non si pareggiano. Una volta identiche, la struttura è perfettamente quadrata. Inchiodare temporaneamente un listello attraverso tre o quattro travetti o borchie per tenerlo quadrato fino a quando non viene fissato in posizione.

Questo è anche un buon modo per controllare che le piastre delle pareti siano quadrate prima di fissarle in posizione prima di iniziare a tagliare le travi del tetto.

Meno di quattro lati da squadrare? Usa il theorum di Pitagora

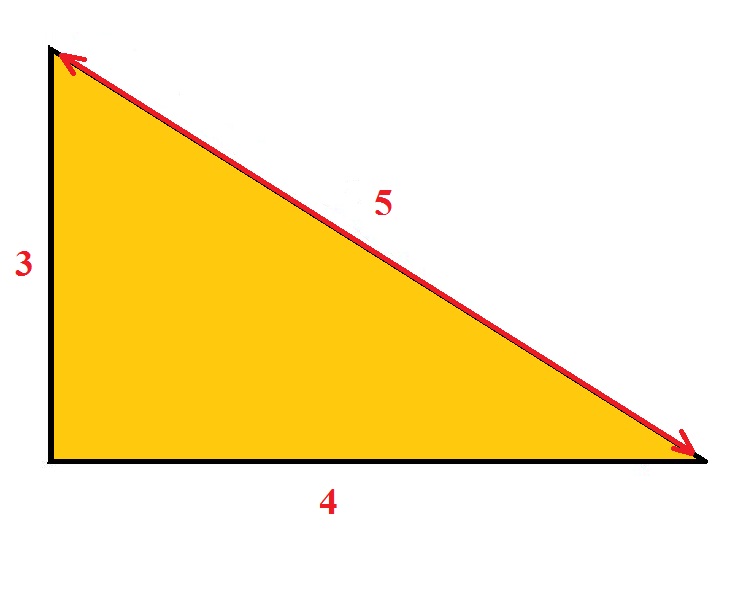
A volte non hai quattro angoli da misurare e quindi è necessario un metodo diverso per verificare la quadratura degli angoli retti. Questo potrebbe essere per esempio quando si costruiscono muri interni e si mettono giù piastre a forma di L. L’immagine qui sotto vi dice tutto quello che dovete sapere per controllare che un telaio, un muro o un’altra struttura sia quadrata usando la regola dei 3 4 5. Quando si misura da un lato 3 e dall’altro 4, la misura tra i due punti dovrebbe essere sempre 5 se l’angolo è di 90 gradi.

Non importa quale unità di misura usi, basta che sia la stessa per tutti e tre i lati. Può essere 3/4/5mm, 3/4/5 piedi, 3/4/5 metri o 3/4/5 miglia!

Quando uso questo metodo per mettere giù due piastre di base, fisso una piastra in posizione e muovo l’altra intorno fino ad ottenere un perfetto ‘5’ e poi fisso anche quella.

La ragione per cui questo funziona è a causa dell’antico controllo della formula quadrata – Pythagorus theorum. Cioè 3 al quadrato, più 4 al quadrato = 5 al quadrato. 3 x 3 = 9, 4 x 4 = 16. Aggiungili insieme e ottieni 25 che è anche 5 x 5.

Ci sono anche molti tipi diversi di squadre da carpentiere disponibili per controllare la quadratura su una scala più piccola e per segnare le linee quadrate quando si imposta.