dei valori minimi & massimi
Parte I
Uno degli usi più importanti del calcolo è determinare i valori minimi e massimi. Questo ha le sue applicazioni nella produzione, nella finanza, nell’ingegneria e in una serie di altri settori. Prima di esaminare un esempio del mondo reale, dovremmo imparare come calcolare tali valori.
Utilizziamo come primo esempio l’equazione 2X2 -5X -7 = 0
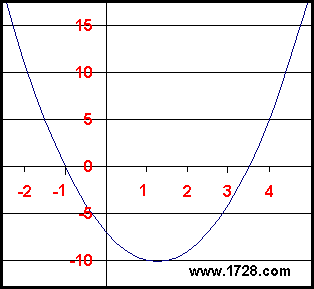
Questa è un’equazione quadratica in una variabile. Cioè è un’equazione della forma:
Con equazioni di questo tipo, sappiamo che quando il termine “a” è positivo, il grafico della curva sarà “concavo verso l’alto” (U-Shaped) e quindi l’equazione avrà un valore minimo ma nessun valore massimo (ok – tecnicamente, il valore massimo è infinito). Guardando il grafico vediamo che il punto minimo è approssimativamente X = 1,5 e Y = -10. C’è un modo per determinare il punto minimo senza graficare l’equazione e ottenere un valore esatto? Sì, c’è!
Guarda il grafico. Se i valori di pendenza fossero calcolati per i punti sul lato sinistro della curva, potresti vedere che la pendenza sarebbe sempre negativa, ma diventa “meno negativa” quanto più la curva si avvicina al minimo (il fondo). Se la pendenza fosse calcolata lungo il lato destro della curva, il valore sarebbe sempre positivo e i valori della pendenza diventerebbero più grandi quanto più i punti sono lontani dal “fondo”.
Quindi, è logico pensare che la pendenza è zero in quel punto “fondo” e quindi anche la derivata è zero in quel punto.
Prendiamo quindi la derivata di 2X2 -5X -7 = 0 che è:
In questo esempio sapevamo che stavamo ottenendo un valore minimo perché lo abbiamo graficato. Inoltre, abbiamo detto che la “regola” per le equazioni quadratiche è tale che quando il termine ‘a’ è positivo, la curva sarà “concava verso l’alto”. C’è ancora un terzo metodo per determinare se un punto è un valore massimo o minimo.
Se prendiamo la derivata seconda e se questo valore è positivo, allora abbiamo a che fare con un valore minimo.
In questo esempio, prendendo la derivata della derivata abbiamo il valore 4 che è positivo e quindi sappiamo che questo è un minimo.
Per le equazioni del tipo aX2 + bX + c =0, un comodo strumento da usare è la Calcolatrice di equazioni quadratiche. Non solo calcola le radici dell’equazione, ma mostra anche la derivata e il punto in cui esiste il massimo o il minimo.
Il secondo esempio che vedremo è molto simile al precedente, tranne che è “concavo verso il basso” invece che “concavo verso l’alto”. Se pensi di aver capito i concetti presentati finora, allora passa alla Parte II
Ok, esaminiamo questa equazione:
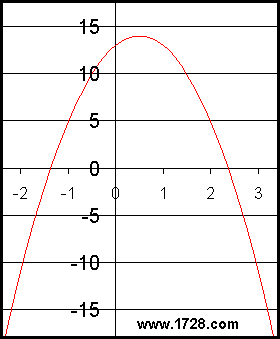
Abbiamo imparato dal primo esempio che il modo per calcolare un punto massimo (o minimo) è trovare il punto in cui la derivata di un’equazione è uguale a zero.La derivata di questa equazione è:
0 commenti