|
Per definizione, la pendenza o il gradiente di una linea descrive la sua ripidità, inclinazione o grado.
Dove
m – pendenza
θ – angolo di pendenza |
 |

Se i 2 punti sono noti
Se 1 punto e la pendenza sono noti
Pendenza, a volte indicato come gradiente in matematica, è un numero che misura la ripidità e la direzione di una linea, o di una sezione di una linea che collega due punti, ed è solitamente indicato con m. Generalmente, la ripidità di una linea è misurata dal valore assoluto della sua pendenza, m. Più grande è il valore, più ripida è la linea. Dato m, è possibile determinare la direzione della linea che m descrive in base al suo segno e valore:
- Una linea è crescente, e va verso l’alto da sinistra a destra quando m > 0
- Una linea è decrescente, e va verso il basso da sinistra a destra quando m < 0
- Una linea ha pendenza costante, ed è orizzontale quando m = 0
- Una linea verticale ha una pendenza indefinita, poiché risulterebbe in una frazione con 0 come denominatore. Fare riferimento all’equazione fornita di seguito.
La pendenza è essenzialmente il cambiamento in altezza rispetto al cambiamento nella distanza orizzontale, ed è spesso indicata come “salita su corsa”. Ha applicazioni nei gradienti in geografia così come nell’ingegneria civile, come la costruzione di strade. Nel caso di una strada il “rialzo” è il cambiamento di altitudine, mentre la “corsa” è la differenza di distanza tra due punti fissi, sempre che la distanza per la misurazione non sia abbastanza grande che la curvatura della terra debba essere considerata come un fattore. La pendenza è rappresentata matematicamente come:
| m = |
y2 – y1 |
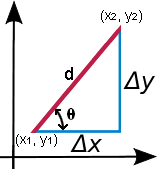
Nell’equazione sopra, y2 – y1 = Δy, o cambiamento verticale, mentre x2 – x1 = Δx, o cambiamento orizzontale, come mostrato nel grafico fornito. Si può anche vedere che Δx e Δy sono segmenti di linea che formano un triangolo rettangolo con ipotenusa d, dove d è la distanza tra i punti (x1, y1) e (x2, y2). Poiché Δx e Δy formano un triangolo rettangolo, è possibile calcolare d usando il teorema di Pitagora. Fai riferimento alla Calcolatrice di Triangoli per maggiori dettagli sul teorema di Pitagora e su come calcolare l’angolo di inclinazione θ fornito nella calcolatrice di cui sopra. Brevemente:
d = √(x2 – x1)2 + (y2 – y1)2
L’equazione di cui sopra è il teorema di Pitagora alla sua radice, dove l’ipotenusa d è già stata risolta, e gli altri due lati del triangolo sono determinati dalla sottrazione dei due valori x e y dati da due punti. Dati due punti, è possibile trovare θ usando la seguente equazione:
m = tan(θ)
Dati i punti (3,4) e (6,8) trovare la pendenza della linea, la distanza tra i due punti e l’angolo di inclinazione:
| m = |
8 – 4 |
= |
d = √(6 – 3)2 + (8 – 4)2 = 5
| = tan(θ) |
| θ = tan-1( | ) = 53.13° |
Anche se questo va oltre lo scopo di questa calcolatrice, a parte il suo uso lineare di base, il concetto di pendenza è importante nel calcolo differenziale. Per le funzioni non lineari, il tasso di cambiamento di una curva varia, e la derivata di una funzione in un dato punto è il tasso di cambiamento della funzione, rappresentato dalla pendenza della linea tangente alla curva in quel punto.
0 commenti