Cosa sono gli stiramenti e le contrazioni orizzontali?
L’allungamento e il restringimento orizzontali, rispettivamente, tirano orizzontalmente il grafico di base, o lo spingono insieme, lasciando invariata l’intercetta y per ancorare il grafico.
Definizione
Per la funzione base f (x) e una costante k, dove k > 0 e k ≠ 1, la funzione data da
g(x) = f (kx),
può essere abbozzata restringendo orizzontalmente f (x) di un fattore 1/k se k > 1
o
allungando orizzontalmente f (x) di un fattore 1/k
se 0 < k < 1.
Un allungamento o restringimento orizzontale di un fattore 1/k significa che il punto (x, y) sul grafico di f(x) si trasforma nel punto (x/k, y) sul grafico di g(x).
Esempi di allungamenti e restringimenti orizzontali
Considerate le seguenti funzioni base,
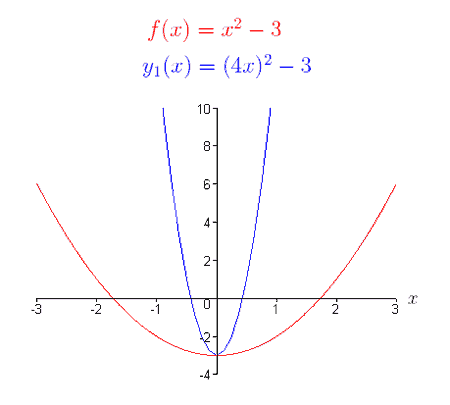
(1) f (x) = x2 – 3,
(2) g(x) = cos (x).
La rappresentazione grafica della funzione (1), f (x), è una parabola. Come supponi che sia il grafico di
y1(x) = f (4x)
? Usando la definizione di f (x), possiamo scrivere y1(x) come,
y1(x) = f (4x) = (4x)2 – 3 = 16×2-3.
In base alla definizione di restringimento orizzontale, il grafico di y1(x) dovrebbe assomigliare al grafico di
f (x), ristretto orizzontalmente di un fattore 1/4. Guarda i grafici di f (x) e y1(x).
La funzione (2), g (x), è una funzione coseno. Come sarebbe il grafico di
y2(x) = g(2/3x)
? Usando la nostra conoscenza degli allungamenti orizzontali, il grafico di y2(x) dovrebbe assomigliare al grafico base g(x) allungato orizzontalmente di un fattore 3/2. Per verificarlo, possiamo scrivere y2(x) come,
y2(x) = g(2/3x) = cos (2/3x),
costruire una tabella di valori e tracciare il grafico della nuova funzione. Come potete vedere, il grafico di y2(x) è in effetti il grafico di base g(x) allungato orizzontalmente di un fattore 3/2.

0 commenti