- Définir la demi-vie.
- Déterminer la quantité de substance radioactive restante après un nombre donné de demi-vies.
Le fait qu’un isotope donné soit radioactif ou non est une caractéristique de cet isotope particulier. Certains isotopes sont stables indéfiniment, tandis que d’autres sont radioactifs et se désintègrent par une forme d’émission caractéristique. Au fil du temps, l’isotope radioactif est de moins en moins présent et le niveau de radioactivité diminue. Un aspect intéressant et utile de la désintégration radioactive est la demi-vie, qui correspond au temps nécessaire pour que la moitié d’un isotope radioactif se désintègre. La demi-vie d’un isotope radioactif spécifique est constante ; elle n’est pas affectée par les coTnditions et est indépendante de la quantité initiale de cet isotope.
Considérez l’exemple suivant. Supposons que nous ayons 100,0 g de tritium (un isotope radioactif de l’hydrogène). Sa demi-vie est de 12,3 ans. Après 12,3 ans, la moitié de l’échantillon se sera désintégrée de l’hydrogène-3 en hélium-3 en émettant une particule bêta, de sorte qu’il ne restera que 50,0 g du tritium d’origine. Après 12,3 années supplémentaires, soit un total de 24,6 années, une autre moitié du tritium restant se sera désintégrée, laissant 25,0 g de tritium. Après 12,3 autres années – soit un total de 36,9 années – une autre moitié du tritium restant se sera désintégrée, laissant 12,5 g. Cette séquence d’événements est illustrée à la figure 15.1 » Décroissance radioactive « .
Figure 15.1 Décroissance radioactive
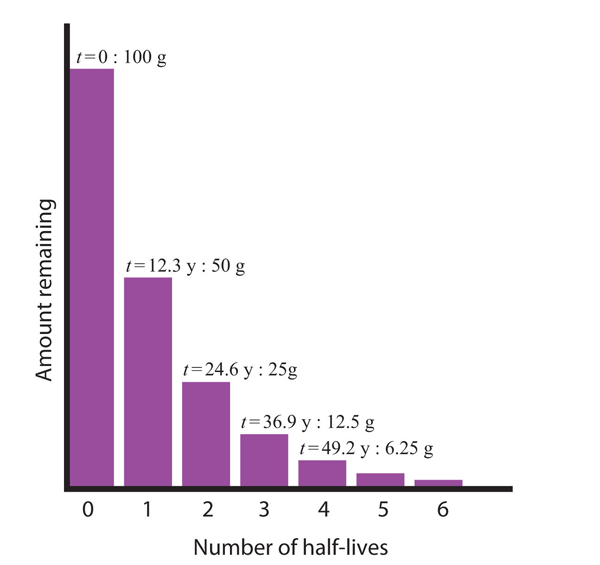
Au cours de chaque demi-vie successive, la moitié de la quantité initiale se désintégrera de manière radioactive.
On peut déterminer la quantité d’un isotope radioactif restant après un nombre donné de demi-vies en utilisant l’expression suivante :
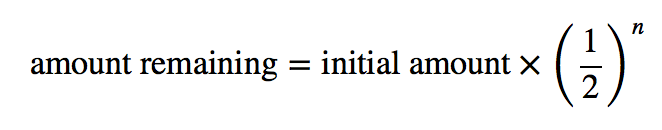
où n est le nombre de demi-vies. Cette expression fonctionne mieux lorsque le nombre de demi-vies est un nombre entier.
Exemple 3
La demi-vie du fluor-20 est de 11,0 s. Si un échantillon contient initialement 5,00 g de fluor-20, combien en reste-t-il après 44.0 s?
Solution
Si l’on compare le temps écoulé à la demi-vie de l’isotope, on constate que 44,0 s correspondent exactement à 4 demi-vies, donc en utilisant l’expression précédente, n = 4. En substituant et en résolvant, on obtient ce qui suit :

Moins d’un tiers de gramme de fluor-20 reste.
Testez-vous
La demi-vie du titane-44 est de 60,0 y. Un échantillon de titane contient 0,600 g de titane-44. Quelle quantité reste-t-il après 240,0 ans ?
Réponse
0,0375 g
Les demi-vies des isotopes vont de fractions de microseconde à des milliards d’années. Le tableau 15.2 « Demi-vies de divers isotopes » énumère les demi-vies de certains isotopes.
Tableau 15.2 Demi-vies de divers isotopes
| Isotope | Mi-vie |
|---|---|
| 3H | 12.3 y |
| 14C | 5730 y |
| 40K | 1,26 × 109 y |
| 51Cr | 27.70 d |
| 90Sr | 29,1 y |
| 131I | 8,04 d |
| 222Rn | 3.823 d |
| 235U | 7,04 × 108 y | 238U | 4.47 × 109 y | 241Am | 432,7 y | 248Bk | 23.7 h |
| 260Sg | 4 ms |
La chimie est partout : Les éléments radioactifs dans le corps
Vous ne vous pensez peut-être pas radioactif, mais vous l’êtes. Une petite partie de certains éléments du corps humain sont radioactifs et subissent constamment une désintégration. Le tableau suivant résume la radioactivité dans le corps humain normal.
| Isotope radioactif | Half-Vie (y) | Masse de l’isotope dans le corps (g) | Activité dans le corps (désintégrations/s) | |
|---|---|---|---|---|
| 40K | 1.26 × 109 | 0,0164 | 4 340 | |
| 14C | 5 730 | 1.6 × 10-8 | 3 080 | 87Rb | 4,9 × 1010 | 0,19 | 600 | 210Pb | 22.3 | 5,4 × 10-10 | 15 |
| 3H | 12,3 | 2 × 10-14 | 7 | |
| 238U | 4.47 × 109 | 1 × 10-4 | 5 | |
| 228Ra | 5,76 | 4,6 × 10-14 | 5 | 226Ra | 1,620 | 3.6 × 10-11 | 3 |
Le corps humain moyen subit environ 8 000 désintégrations radioactives/s.
La majeure partie de la radioactivité du corps humain provient du potassium 40 et du carbone 14. Le potassium et le carbone sont deux éléments dont nous ne pouvons absolument pas nous passer, donc à moins de pouvoir éliminer tous les isotopes radioactifs de ces éléments, il n’y a aucun moyen d’échapper au moins à une partie de la radioactivité. La question de savoir quel élément radioactif est le plus problématique fait l’objet d’un débat. Il y a plus de potassium 40 dans l’organisme que de carbone 14, et sa demi-vie est beaucoup plus longue. Le potassium 40 se désintègre également avec environ 10 fois plus d’énergie que le carbone 14, ce qui rend chaque désintégration potentiellement plus problématique. Cependant, le carbone est l’élément qui constitue l’épine dorsale de la plupart des molécules vivantes, ce qui rend le carbone 14 plus susceptible d’être présent autour de molécules importantes, comme les protéines et les molécules d’ADN. La plupart des experts s’accordent à dire que s’il est téméraire de ne s’attendre à aucune exposition à la radioactivité, nous pouvons et devons minimiser l’exposition à une radioactivité excessive.
Et si le temps écoulé n’est pas un nombre exact de demi-vies ? Nous pouvons toujours calculer la quantité de matière qui nous reste, mais l’équation est plus compliquée. L’équation est
où e est la base des logarithmes naturels (2,71828182…), t est le temps écoulé et t1/2 est la demi-vie de l’isotope radioactif. Les variables t et t1/2 doivent avoir les mêmes unités de temps, et vous devrez peut-être vous assurer que vous savez comment évaluer les puissances des logarithmes naturels sur votre calculatrice (pour de nombreuses calculatrices, il existe une fonction » logarithme inverse » que vous pouvez utiliser ; consultez votre instructeur si vous n’êtes pas sûr de savoir comment utiliser votre calculatrice). Bien qu’il s’agisse d’une formule plus compliquée, la durée t n’a pas besoin d’être un multiple exact des demi-vies.
Exemple 4
La demi-vie du fluor-20 est de 11,0 s. Si un échantillon contient initialement 5,00 g de fluor-20, combien en reste-t-il après 60,0 s ?
Solution
Bien que similaire à l’exemple 3, la durée n’est pas un multiple exact d’une demi-vie. Ici, nous identifions la quantité initiale comme étant 5,00 g, t = 60,0 s et t1/2 = 11,0 s. En substituant dans l’équation :
la quantité restante = (5,00 g) × e-(0,693)(60,0 s)/11,0 s
En évaluant l’exposant (et en notant que les unités s s’annulent), nous obtenons
la quantité restante = (5.00 g) × e-3,78
En résolvant, la quantité restante est de 0,114 g. (Vous pouvez vérifier cette réponse pour confirmer que vous utilisez correctement votre calculatrice.)
Testez vous-même
La demi-vie du titane-44 est de 60,0 y. Un échantillon de titane contient 0,600 g de titane-44. Combien en reste-t-il après 100,0 ans ?
Réponse
0,189 g
Principaux enseignements
- Les processus radioactifs naturels sont caractérisés par une demi-vie, c’est-à-dire le temps nécessaire pour que la moitié de la matière se désintègre de manière radioactive.
- On peut facilement calculer la quantité de matière restante après un certain nombre de demi-vies.
Exercices
-
Tous les isotopes ont-ils une demi-vie ? Expliquez votre réponse.
-
Qu’est-ce qui est le plus radioactif-un isotope avec une longue demi-vie ou un isotope avec une courte demi-vie ?
-
Combien de temps faut-il à 1,00 g de palladium-103 pour se désintégrer en 0,125 g si sa demi-vie est de 17,0 d ?
-
Combien de temps faut-il à 2.00 g de niobium-94 pour se désintégrer en 0,0625 g si sa demi-vie est de 20 000 y?
-
Il a fallu 75 y pour que 10,0 g d’un isotope radioactif se désintègre en 1.25 g. Quelle est la demi-vie de cet isotope ?
-
Il a fallu 49,2 s pour que 3,000 g d’un isotope radioactif se désintègre en 0,1875 g. Quelle est la demi-vie de cet isotope ?
-
La demi-vie de l’américium-241 est de 432 y. Si 0,0002 g d’américium-241 est présent dans un détecteur de fumée à la date de fabrication, quelle masse d’américium-241 est présente après 100,0 y ? Après 1 000,0 y?
-
Si la demi-vie du tritium (hydrogène-3) est de 12,3 y, quelle masse d’un échantillon de 0,00444 g de tritium est présente après 5,0 y ? Après 250,0 y?
-
Expliquez pourquoi la quantité restante après 1 000,0 y dans l’exercice 7 n’est pas un dixième de la quantité présente après 100,0 y, malgré le fait que la quantité de temps écoulé soit 10 fois plus longue.
-
Expliquez pourquoi la quantité restante après 250.0 y dans l’exercice 8 n’est pas un cinquantième de la quantité présente après 5,0 y, malgré le fait que la quantité de temps écoulé soit 50 fois plus longue.
-
Un artefact contenant du carbone 14 en contient 8,4 × 10-9 g. Si l’âge de l’artefact est de 10 670 y, quelle quantité de carbone-14 avait-il à l’origine ? La demi-vie du carbone-14 est de 5 730 ans.
-
Le carbone-11 est un isotope radioactif utilisé dans la tomographie par émission de positons (TEP) pour le diagnostic médical. L’émission de positrons est un autre type de radioactivité, bien que rare. La demi-vie du carbone 11 est de 20,3 minutes. Si 4,23 × 10-6 g de carbone-11 restent dans le corps après 4,00 h, quelle masse de carbone-11 était présente initialement ?
Réponses
Seuls les isotopes radioactifs ont une demi-vie.
51,0 d
25 ans
0,000170 g ; 0,0000402 g
La décroissance radioactive est un processus exponentiel et non linéaire.
3,1 × 10-8 g
.
0 commentaire